1.2: Campos de taludes

La ecuación general de primer orden que estamos estudiando parece

\[ y' = f(x,y) \nonumber \]

En general, no podemos simplemente resolver este tipo de ecuaciones explícitamente. Sería bueno que al menos pudiéramos averiguar la forma y el comportamiento de las soluciones, o si pudiéramos encontrar soluciones aproximadas. En este punto puede ser bueno probar primero el Laboratorio I y/o el Proyecto I desde el sitio web del IODE.

Campos de taludes

La ecuación te\(y' = f(x,y)\) da una pendiente en cada punto del\((x,y)\) plano. Y esta es la pendiente a la que\(y(x)\) tendría una solución\(x\) si su valor fuera\(y\). En otras palabras,\(f(x,y)\) es la pendiente de una solución cuya gráfica recorre el punto\((x,y)\). En un punto\((x,y)\), trazamos una línea corta con la pendiente\(f(x,y)\). Por ejemplo, si\(f(x,y) = xy\), entonces en el punto\((2,1.5)\) dibujamos una línea corta de pendiente\(xy = 2 \times 1.5 = 3\). Entonces, si\(y(x)\) es una solución y\(y(2) = 1.5\), entonces la ecuación lo ordena\(y'(2) = 3\). Ver Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): La pendiente\(y'=xy\) en\((2,1.5)\).

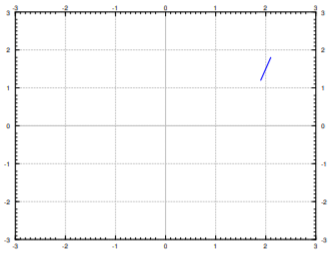
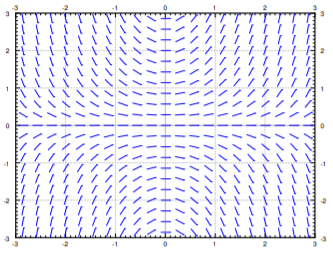
Para tener una idea de cómo se comportan las soluciones, dibujamos tales líneas en muchos puntos del avión, no solo en el punto\((2,1.5)\). Lo ideal sería que quisiéramos ver la pendiente en cada punto, pero eso simplemente no es posible. Por lo general, elegimos una cuadrícula de puntos lo suficientemente fina como para que muestre el comportamiento, pero no demasiado fina para que aún podamos reconocer las líneas individuales. Llamamos a este cuadro el de la ecuación. Ver Figura\(\PageIndex{2}\) para el campo de pendiente de la ecuación\(y' = xy\). Por lo general en la práctica, uno no hace esto a mano, sino que tiene una computadora que haga el dibujo.

Supongamos que se nos da una condición inicial específica\(y(x_0) = y_0\). Una solución, es decir, la gráfica de la solución, sería una curva que siga las pendientes que dibujamos. Para algunas soluciones de muestra, ver Figura\(\PageIndex{3}\). Es fácil esbozar aproximadamente (o al menos imaginar) posibles soluciones en el campo de pendiente, solo con mirar el campo de pendiente en sí. Simplemente dibuja una línea que se ajuste aproximadamente a los pequeños segmentos de línea y pase por su condición inicial.

Figura\(\PageIndex{3}\): Campo de pendiente de\(y'=xy\).

Figura\(\PageIndex{3}\): Sl ope campo de\( y' = xy \) con una gráfica de soluciones satisfactorias\( y(0) = 0.2\),\( y(0) = 0\), y\(y(0) = -0.2\).

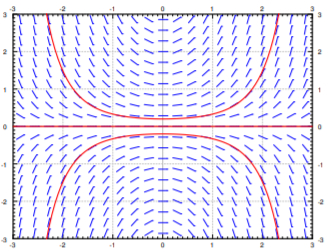
Al mirar el campo de pendiente obtenemos mucha información sobre el comportamiento de las soluciones sin tener que resolver la ecuación. Por ejemplo, en Figura\(\PageIndex{3}\) vemos lo que hacen las soluciones cuando son las condiciones iniciales\(y(0) > 0\),\(y(0) = 0\) y\(y(0) < 0\). Un pequeño cambio en la condición inicial provoca un comportamiento bastante diferente. Vemos este comportamiento solo desde el campo de pendiente e imaginando qué soluciones deberían hacer.

Vemos un comportamiento diferente para la ecuación\(y' = -y\). El campo de pendiente y algunas soluciones se encuentra en ver Figura\(\PageIndex{4}\). Si pensamos en movernos de izquierda a derecha (quizás\(x\) es tiempo y el tiempo suele aumentar), entonces vemos que no importa lo que\(y(0)\) sea, todas las soluciones tienden a cero como\(x\) tiende al infinito. Nuevamente ese comportamiento es claro por el simple hecho de mirar el propio campo de pendiente.

Figura\(\PageIndex{4}\): Campo de pendiente de\( y' = -y\) with a graph of a few solutions.

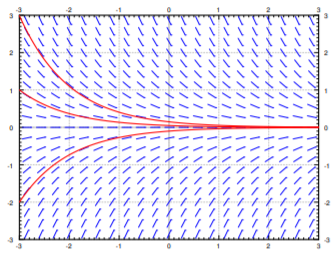
Existencia y singularidad

Deseamos hacer dos preguntas fundamentales sobre el problema

\[ y' = f(x,y),\quad y(x_0) = y_0 \nonumber \]

1. ¿Existe una solución?
2. ¿La solución es única (si existe)?

¿Cuál crees que es la respuesta? La respuesta parece ser sí a ambos ¿no? Bueno, más o menos. Pero hay casos en los que la respuesta a cualquiera de las dos preguntas puede ser no.

Dado que generalmente las ecuaciones que encontramos en las aplicaciones provienen de situaciones de la vida real, parece lógico que siempre exista una solución. También tiene que ser único si creemos que nuestro universo es determinista. Si la solución no existe, o si no es única, probablemente no hayamos ideado el modelo correcto. De ahí que sea bueno saber cuándo van mal las cosas y por qué.

Ejemplo\(\PageIndex{1}\)

Intento de resolver

\[ y' = \dfrac {1}{x}, \quad y(0) = 0. \nonumber \]

Solución

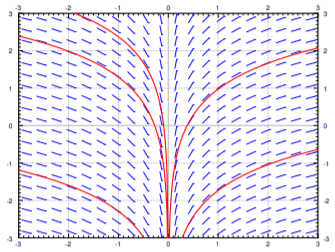
Integrar para encontrar la solución general\( y = \ln \left \vert x \right \vert + C\). Tenga en cuenta que la solución no existe en\( x = 0 \). Ver Figura\(\PageIndex{5}\) on the following page. The equation may have been written as the seemingly harmless \(xy'=1\).

Figura\(\PageIndex{5}\): Campo de pendiente de\(y' = \dfrac{1}{x}.\)

Ejemplo\(\PageIndex{2}\)

Resolver:

\[ y' = 2 \sqrt {\left \vert y \right \vert}, \quad y(0) = 0 . \nonumber \]

Solución

Figura\(\PageIndex{6}\): Campo de pendiente de\( y' = 2 \sqrt{|y|}\) con dos soluciones satisfactorias\( y(0)=0.\)

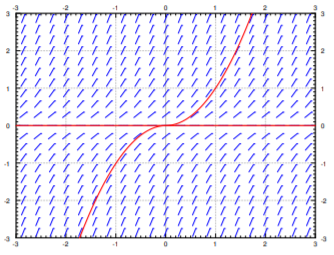
Tenga en cuenta que\( y = 0 \) es una solución. Pero otra solución es la función

\[ y(x) =\begin {cases} x^2 & {\rm{if~}} x \ge 0 \\ -x^2 & {\rm{if~}} x < 0 \end {cases} \nonumber \]

Es difícil decir al mirar el campo de pendiente que la solución no es única. ¿Hay alguna esperanza? Por supuesto que sí. Tenemos el siguiente teorema, conocido como teorema de Picard. \(^{1}\)

Teorema\(\PageIndex{1}\)

Teorema de Picard sobre la existencia y la singularidad

Si\( f(x,y) \) es continuo (en función de dos variables) y\(\dfrac{\partial f}{\partial y}\) existe y es continuo cerca de algunas \( (x_0,y_0)\), luego una solución para

\[y'=f(x,y),\quad y(x_{0})=y_{0} \nonumber \]

existe (al menos para\(x\) in some small interval) y es único.

Nótese que los problemas\(y' = \dfrac{1}{x}\)\( y' = 2 \sqrt {\left \vert y \right \vert}\),\( y(0) = 0 \) y,\( y(0) = 0 \) no satisfacen la hipótesis del teorema. Aunque podamos usar el teorema, debemos tener cuidado con este negocio de existencia. Es muy posible que la solución sólo exista por un corto tiempo.

Ejemplo\(\PageIndex{3}\)

Para alguna constante\(A\), resuelve:

\[ y' = y^2\quad y(0) = A \nonumber \].

Solución

Sabemos resolver esta ecuación. Primero supongamos que\( A \ne 0\), por lo tanto no\(y\) es igual a cero al menos para algunos\(x\) cerca de 0. Entonces\( x' = \dfrac{1}{y^2}\), entonces\(x = -\dfrac{1}{y} + C\), entonces\(y = \dfrac {1}{C - x}\). Si\( y(0) = A \), entonces\( C = \dfrac{1}{A}\) así

\[ y = \dfrac {1}{\dfrac{1}{A} - x} \nonumber \]

Si\( A = 0\), entonces\( y = 0 \) es una solución.

Por ejemplo, cuando\(A = 1\) la solución “estalla” en\(x = 1\). De ahí que la solución no exista para todos\(x\) aunque la ecuación sea agradable en todas partes. La ecuación\(y' = y^2\) ciertamente se ve bien.

Para la mayor parte de este curso nos interesarán las ecuaciones donde se sostiene la existencia y la singularidad, y de hecho se sostiene “globalmente” a diferencia de la ecuación\(y' = y^2\).

Notas al pie

[1] El nombre del matemático francés Charles Émile Picard (1856 — 1941)