1.6: Ecuaciones autónomas
- Page ID
- 115497
Consideremos problemas generales de ecuación diferencial de la forma
\[ \dfrac{dx}{dt} = f(x) \nonumber \]
donde la derivada de soluciones depende únicamente de\(x\) (la variable dependiente). Tales ecuaciones se denominan ecuaciones autónomas. Si pensamos en el\(t\) tiempo, el naming viene del hecho de que la ecuación es independiente del tiempo.
Volvamos al problema del café de enfriamiento (ver Ejemplo 1.3.3). La ley de enfriamiento de Newton dice que
\[ \dfrac{dx}{dt} = -k(x-A) \nonumber \]
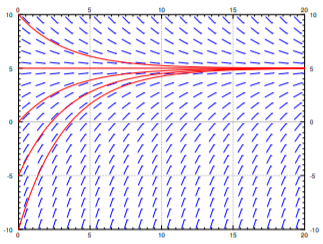
donde\(x\) esta la temperatura,\(t\) es el tiempo,\(k\) es algo constante, y\(A\) es la temperatura ambiente. Ver Figura\(\PageIndex{1}\) para un ejemplo con\(k = 0.3\) y\(A = 5\).
Anote la solución\(x = A\) (en la figura\(x = 5\)). Llamamos a estas soluciones constantes las soluciones de equilibrio. Los puntos en el\(x\) eje donde\(f(X) = 0\) se denominan puntos críticos. El punto\(x = A\) es un punto crítico. De hecho, cada punto crítico corresponde a una solución de equilibrio. Tenga en cuenta también, al mirar la gráfica, que la solución\(x = A\) es “estable” en que pequeñas perturbaciones en\(x\) no conducen a soluciones sustancialmente diferentes a medida que\(t\) crece. Si cambiamos un poco la condición inicial, entonces a medida\(t \rightarrow \infty \) que obtenemos\(x \rightarrow A\). Llamamos a esos puntos críticos estables. En este sencillo ejemplo resulta que todas las soluciones de hecho van a\(A\) como\( t \rightarrow \infty\). Si un punto crítico no es estable diríamos que es inestable.
Consideremos la ecuación logística
\[ \dfrac{dx}{dt} = kx(M-x) \nonumber \]
para algunos positivos\(k\) y\(M\). Esta ecuación es comúnmente utilizada para modelar población si conocemos la población limitante\(M\), es decir, la población máxima sustentable. La ecuación logística conduce a predicciones menos catastróficas sobre la población mundial que\(x'=kx\). En el mundo real no existe tal cosa como población negativa, pero seguiremos considerándolo negativo\(x\) a los efectos de las matemáticas (ver Figura\(\PageIndex{2}\) para un ejemplo).
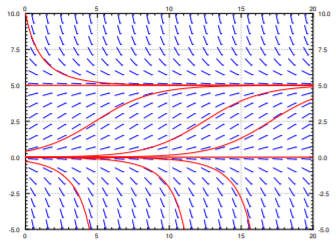
Anote dos puntos críticos,\(x = 0\) y\(x = 5\). El punto crítico at\(x = 5\). es estable. Por otro lado el punto crítico at\(x = 0\). es inestable.
No es realmente necesario encontrar las soluciones exactas para hablar sobre el comportamiento a largo plazo de las soluciones. Por ejemplo, a partir de la parcela de campo de pendiente anterior, podemos ver fácilmente que
\[\lim\limits_{t\to\infty} x(t) = \begin{cases} 5 & \text{if} \, x(0) > 0, \\ 0 & \text{if} \, x(0) = 0, \\ \text{DNE or} -\infty & \text{if} \, x(0) < 0. \end{cases} \nonumber \]
Donde DNE significa “no existe”. De solo mirar el campo de pendiente no podemos decidir del todo qué pasa si\(x(0) < 0\). Podría ser que la solución no exista para\(t\) todo el camino a\(\infty\). Piensa en la ecuación\(x' = x^2\), hemos visto que solo existe por algún periodo finito de tiempo. Lo mismo puede pasar aquí. En nuestra ecuación de ejemplo anterior realmente resultará que la solución no existe para siempre, sino para ver que tendríamos que resolver la ecuación. En cualquier caso, la solución sí va a\(- \infty\), pero puede llegar allí con bastante rapidez.
Si sólo nos interesa el comportamiento a largo plazo de la solución, estaríamos haciendo un trabajo innecesario si resolviéramos exactamente la ecuación. Podríamos dibujar el campo de pendiente, pero es más fácil simplemente mirar el o, que es una forma sencilla de visualizar el comportamiento de las ecuaciones autónomas. En este caso hay una variable dependiente\(x\). Dibujamos el\(x\) eje -eje, marcamos todos los puntos críticos, y luego dibujamos flechas en el medio. Ya que\(x\) es la variable dependiente dibujamos el eje verticalmente, tal y como aparece en los diagramas de campo de pendiente anteriores. Si\(f(x) > 0\), dibujamos una flecha hacia arriba. Si\(f(x) < 0\), dibujamos una flecha hacia abajo. Para resolverlo, podríamos simplemente enchufar algunos\(x\) entre los puntos críticos,\(f(x)\) tendremos el mismo signo en absoluto\(x\) entre dos puntos críticos siempre que\(f(x)\) sea continuo. Por ejemplo,\(f(6) = -0.6 < 0\), así\(f(x) < 0\) para\(x > 5\), y la flecha de arriba\(x=5\) es una flecha hacia abajo. A continuación,\(f(1) = 0.4 > 0\), así\(f(x) > 0\) cuando sea\(0 < x < 5\), y la flecha apunta hacia arriba. Por último,\(f(-1) = -0.6 < 0\) así\(f(x) < 0\) cuando\(x < 0\), y la flecha apunta hacia abajo.
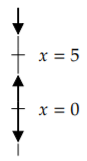
Armado con el diagrama de fases, es fácil esbozar las soluciones aproximadamente: A medida que el tiempo\(t\) se mueve de izquierda a derecha, la gráfica de una solución sube si la flecha está arriba, y baja si la flecha está hacia abajo.
Intente esbozar algunas soluciones simplemente mirando el diagrama de fases. Consulta con las gráficas anteriores si estás obteniendo el tipo de curvas.
Una vez que dibujamos el diagrama de fases, podemos clasificar fácilmente los puntos críticos como estables o inestables. \(^{1}\)

Dado que cualquier modelo matemático que cocinemos sólo será una aproximación al mundo real, los puntos inestables son generalmente malas noticias.
Pensemos en la ecuación logística con la cosecha. Supongamos que a una raza alienígena realmente le gusta comer humanos Mantienen un planeta con humanos en él y cosechan a los humanos a una tasa de\(h\) millones de humanos al año. Supongamos que\(x\) es el número de humanos en millones en el planeta y\(t\) es tiempo en años. Dejar\(M\) ser la población limitante cuando no se realiza ninguna cosecha y\(k>0\) es alguna constante dependiendo de qué tan rápido se multipliquen los humanos. Nuestra ecuación se convierte
\[ \dfrac{dx}{dt} = kx(M-x)-h \nonumber \]
Ampliamos el lado derecho y resolvemos puntos críticos
\[ \dfrac{dx}{dt} = -kx^2+kMx-h \nonumber \]
Resolviendo para los puntos críticos\( A\) y\(B\) a partir de las ecuaciones cuadráticas:
\[ A= \dfrac{kM + \sqrt{(kM)^2-4hk}}{2k},\quad B= \dfrac{kM - \sqrt{(kM)^2-4hk}}{2k} \nonumber \]
Esboce un diagrama de fases para diferentes posibilidades. Tenga en cuenta que estas posibilidades son\(A > B\), o\(A = B\), o\(A\) y\(B\) ambas complejas (es decir, no hay soluciones reales). Pista: Arreglar algunos simples\(k\) y\(M\) y luego variar\(h\).
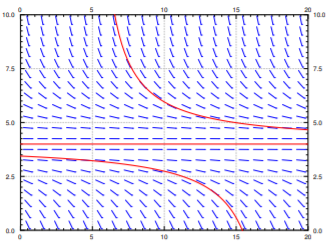
Por ejemplo, vamos\(M=8\) y\(k=0.1\). Cuando\(h=1\), entonces\(A\) y\(B\) son distintos y positivos. El campo de pendiente que obtenemos está en Figura\(\PageIndex{5}\). Mientras la población comience por encima\(B\), que es aproximadamente 1.55 millones, entonces la población no morirá. De hecho, tenderá a\(A \approx 6.45\) millones. Si alguna vez ocurre alguna catástrofe y la población cae por debajo\(B\), los humanos morirán, y el restaurante de comida rápida que los sirve dejará de funcionar.
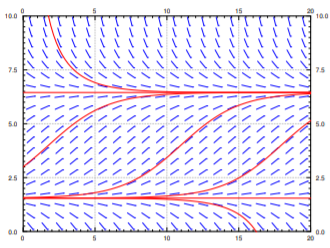
Cuando\(h=1.6\), entonces\(A=B=4\) y solo hay un punto crítico y es inestable. Cuando la población comience por encima de los 4 millones tenderá hacia los 4 millones. Si alguna vez cae por debajo de los 4 millones, los humanos morirán en el planeta. Este escenario no es uno en el que nosotros (como propietario humano de la comida rápida) queramos estar. Una pequeña perturbación del estado de equilibrio y estamos fuera del negocio; no hay margen para el error (ver Figura\(\PageIndex{6}\)).
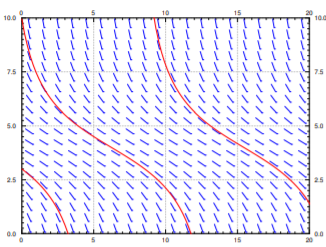
Por último, si estamos cosechando a 2 millones de humanos al año, no hay puntos críticos. La población siempre se desplomará hacia cero, por muy bien abastecido que empiece el planeta (ver Figura\(\PageIndex{7}\)).
Notas al pie
[1] Los puntos inestables con una de las flechas apuntando hacia el punto crítico a veces se denominan semistables.
Referencias
- Paul W. Berg y James L. McGregor, Ecuaciones diferenciales parciales elementales, Holden-Day, San Francisco, CA, 1966.
- William E. Boyce, Richard C. DiPrima, Ecuaciones diferenciales elementales y problemas de valor límite, 9ª edición, John Wiley & Sons Inc., Nueva York, NY, 2008.
- C.H. Edwards y D.E. Penney, Ecuaciones diferenciales y problemas de valor límite: computación y modelado, 4ª edición, Prentice Hall, 2008.
- Stanley J. Farlow, Una introducción a las ecuaciones diferenciales y sus aplicaciones, McGraw-Hill, Inc., Princeton, NJ, 1994. (Publicado también por Dover Publications, 2006.)
- E.L. Ince, Ecuaciones Diferenciales Ordinarias, Dover Publications, Inc., Nueva York, NY, 1956.


