1.7: Métodos numéricos: método de Euler

Última actualización
Guardar como PDF

Page ID: 115498

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En este punto puede ser bueno probar primero el Laboratorio II y/o el Proyecto II desde el sitio web del IODE: www.math.uiuc.edu/iode/. Como dijimos antes, a menos que$f(x, y)$ sea de una forma especial, generalmente es muy difícil si no imposible conseguir una buena fórmula para la solución del problema

\[y' = f(x, y), \, \, \, \, \,\, y(x_0) = y_0 \nonumber \]

Si la ecuación se puede resolver en forma cerrada, deberíamos hacerlo. Pero, ¿y si tenemos una ecuación que no se puede resolver en forma cerrada? ¿Y si queremos encontrar el valor de la solución en algún particular$x$? O tal vez queremos producir una gráfica de la solución para inspeccionar el comportamiento. En esta sección aprenderemos sobre los fundamentos de la aproximación numérica de soluciones.

El método más simple para aproximar una solución es el Método de Euler. $^{1}$Funciona de la siguiente manera: Tomar$x_0$ y computar la pendiente$k = f(x_0,y_0)$. La pendiente es el cambio en el cambio$y$ por unidad en$x$. Siga la línea durante un intervalo de longitud$h$ en el$x$ eje. De ahí que si$y = y_0$ at$x_0$, entonces decimos que$y_1$ (el valor aproximado de$y$ at$x_1 = x_0 + h$) es$y_1 = y_0 + h k$. ¡Enjuaga, repite! Dejar$k = f(x_1,y_1)$, y luego computar$x_2 = x_1 + h$, y$y_2 = y_1 + h k$. Ahora computar$x_3$$x_2$ y$y_3$ usar y$y_2$, etc. Considere la ecuación$y' = \frac{y^2}{3}$,$y(0)=1$, y$h=1$. Entonces$x_0=0$ y$y_0 = 1$. Nosotros computamos

\[\begin{align}\begin{aligned} & x_1 = x_0 + h = 0 + 1 = 1, & & y_1 = y_0 + h \, f(x_0,y_0) = 1 + 1 \cdot \frac{1}{3} = \frac{4}{3} \approx 1.333,\\ & x_2 = x_1 + h = 1 + 1 = 2, & & y_2 = y_1 + h \, f(x_1,y_1) = \frac{4}{3} + 1 \cdot \frac{{(\frac{4}{3})}^2}{3} = \frac{52}{27} \approx 1.926.\end{aligned}\end{align} \nonumber \]

Después dibujamos una gráfica aproximada de la solución conectando los puntos$(x_0,y_0)$,$(x_1,y_1)$,$(x_2,y_2)$,... Para los dos primeros pasos del método ver Figura$\PageIndex{1}$.

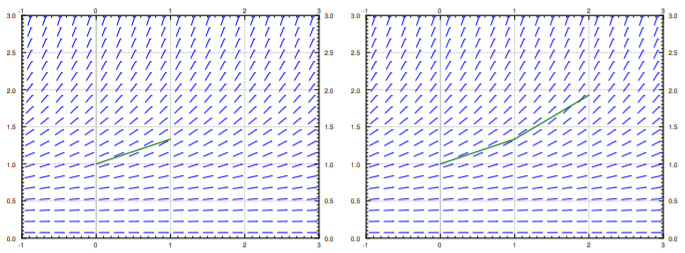
$clipboard_e38b2e84ce68993da1a7d32bb889ee376.png$

Figura$\PageIndex{1}$: Primeros dos pasos del método de Euler con$h=1$ para la ecuación$y'=\frac{y^{2}}{3}$ con condiciones iniciales$y(0)=1$.

Más abstractamente, para cualquier$i=0,1,2,3,\ldots$, calculamos\[x_{i+1} = x_i + h , \qquad y_{i+1} = y_i + h\, f(x_i,y_i) . \nonumber \]

Los segmentos de línea que obtenemos son una gráfica aproximada de la solución. Generalmente no es exactamente la solución. Ver Figura$\PageIndex{2}$ para la gráfica de la solución real y la aproximación.

Figura$\PageIndex{2}$: Dos pasos del método de Euler (tamaño de paso 1) y la solución exacta para la ecuación$y' = \frac{y^2}{3}$ with initial conditions $y(0) = 1$.

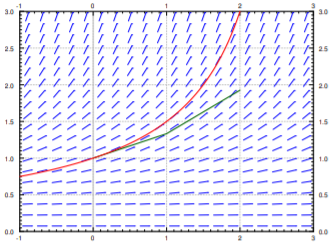
Seguimos con la ecuación$y' = \frac{y^2}{3}$,$y(0)=1$. Intentemos aproximarnos$y(2)$ usando el método de Euler. En Figuras$\PageIndex{1}$ y$\PageIndex{2}$ hemos aproximado gráficamente$y(2)$ con tamaño de paso 1. Con el tamaño de paso 1, tenemos$y(2) \approx 1.926$. La verdadera respuesta es 3. Estamos aproximadamente$1.074$ apagados. Reducimos a la mitad el tamaño del paso. $y_4$Computando con$h=0.5$, nos encontramos con eso$y(2) \approx 2.209$, por lo que un error de aproximadamente$0.791$. Tabla$\PageIndex{1}$ da los valores calculados para diversos parámetros.

Ejercicio$\PageIndex{1}$

Resuelve esta ecuación exactamente y muéstralo$y(2) = 3$.

La diferencia entre la solución real y la solución aproximada llamaremos el error. Por lo general vamos a hablar solo del tamaño del error y no nos importa mucho su signo. El punto principal es, que solemos desconocer la solución real, por lo que sólo tenemos una vaga comprensión del error. Si supiéramos exactamente el error... ¿cuál es el punto de hacer la aproximación?

$h$	Aproximado$y(2)$	Error	$\frac{\text{Error}}{\text{Previous error}}$
\ (h\) ">1	\ (y (2)\) ">1.92593	1.07407	\ (\ frac {\ text {Error}} {\ text {Error anterior}}\) ">
\ (h\) ">0.5	\ (y (2)\) ">2.20861	0.79139	\ (\ frac {\ text {Error}} {\ text {Error anterior}}\) ">0.73681
\ (h\) ">0.25	\ (y (2)\) ">2.47250	0.52751	\ (\ frac {\ text {Error}} {\ text {Error anterior}}\) ">0.66656
\ (h\) ">0.125	\ (y (2)\) ">2.68034	0.31966	\ (\ frac {\ text {Error}} {\ text {Error anterior}}\) ">0.60599
\ (h\) ">0.0625	\ (y (2)\) ">2.82040	0.17960	\ (\ frac {\ text {Error}} {\ text {Error anterior}}\) ">0.56184
\ (h\) ">0.03125	\ (y (2)\) ">2.90412	0.09588	\ (\ frac {\ text {Error}} {\ text {Error anterior}}\) ">0.53385
\ (h\) ">0.015625	\ (y (2)\) ">2.95035	0.04965	\ (\ frac {\ text {Error}} {\ text {Error anterior}}\) ">0.51779
\ (h\) ">0.0078125	\ (y (2)\) ">2.97472	0.02528	\ (\ frac {\ text {Error}} {\ text {Error anterior}}\) ">0.50913

Tabla$\PageIndex{1}$: Aproximación del método de Euler de$y(2)$ dónde de$y' = \frac{y^2}{3}$,$y(0) = 1$.

Notamos que a excepción de las primeras veces, cada vez que redujimos a la mitad el intervalo el error se redujo aproximadamente a la mitad. Esta reducción a la mitad del error es una característica general del método de Euler, ya que es un método de primer orden. En el Proyecto IODE II se le pide implementar un método de segundo orden. Un método de segundo orden reduce el error a aproximadamente un cuarto cada vez que reducimos a la mitad el intervalo (segundo orden as$\frac{1}{4} = \frac{1}{2} \text{x} \frac{1}{2}$).

Para que el error estuviera dentro de 0.1 de la respuesta tuvimos que hacer ya 64 pasos. Para conseguirlo dentro de 0.01 tendríamos que reducir a la mitad otras tres o cuatro veces, es decir, hacer 512 a 1024 pasos. Eso es bastante que hacer a mano. El método mejorado de Euler del Proyecto II de IODE debería trimestrar el error cada vez que reducimos a la mitad el intervalo, por lo que tendríamos que hacer aproximadamente la mitad de “halvings” para obtener el mismo error. Esta reducción puede ser un gran problema. Con 10 halvings (comenzando en$h = 1$) tenemos 1024 pasos, mientras que con 5 halvings sólo tenemos que hacer 32 pasos, asumiendo que el error era comparable para empezar. A una computadora puede no importarle esta diferencia por un problema así de simple, pero supongamos que cada paso tardaría un segundo en computar (la función puede ser sustancialmente más difícil de calcular que$\frac{y^2}{3}$). Entonces la diferencia es de 32 segundos frente a unos 17 minutos. Nota: No estamos siendo del todo justos, un método de segundo orden probablemente duplicaría el tiempo para hacer cada paso. Aun así, es de 1 minuto frente a 17 minutos. A continuación, supongamos que tenemos que repetir un cálculo de este tipo para diferentes parámetros mil veces. Se te da la idea.

¡Tenga en cuenta que en la práctica no sabemos qué tan grande es el error! ¿Cómo sabemos cuál es el tamaño de paso correcto? Bueno, esencialmente seguimos reduciendo a la mitad el intervalo, y si tenemos suerte, podemos estimar el error a partir de algunos de estos cálculos y la suposición de que el error baja por un factor de la mitad cada vez (si estamos usando Euler estándar).

Ejercicio$\PageIndex{2}$

En la tabla anterior, supongamos que no conoce el error. Tome los valores aproximados de la función en las dos últimas líneas, asuma que el error baja por un factor de 2. ¿Se puede estimar el error en la última vez a partir de esto? ¿Está (aproximadamente) de acuerdo con la mesa? Ahora hazlo para las dos primeras filas. ¿Esto concuerda con la mesa?

Hablemos un poco más sobre el ejemplo$y' = \frac{y^2}{3}$,$y(0) = 1$. Supongamos que en vez del valor que$ y(2)$ deseamos encontrar$y(3)$. Los resultados de este esfuerzo se listan en Tabla$\PageIndex{2}$ para halvings sucesivos de$h$. ¿Qué está pasando aquí? Bueno, deberías resolver la ecuación exactamente y notarás que la solución no existe en$x =3$. De hecho, la solución va al infinito cuando te acercas$x =3$.

$h$	Aproximado$y(3)$
\ (h\) ">1	\ (y (3)\) ">3.16232
\ (h\) ">0.5	\ (y (3)\) ">4.54329
\ (h\) ">0.25	\ (y (3)\) ">6.86079
\ (h\) ">0.125	\ (y (3)\) ">10.80321
\ (h\) ">0.0625	\ (y (3)\) ">17.59893
\ (h\) ">0.03125	\ (y (3)\) ">29.46004
\ (h\) ">0.015625	\ (y (3)\) ">50.40121
\ (h\) ">0.0078125	\ (y (3)\) ">87.75769

Tabla$\PageIndex{2}$: Intentos de usar Euler's para aproximar$y(3)$ dónde de$y' = \frac{y^2}{3}$,$y(0) = 1$.

Otro caso en el que las cosas pueden ir mal es si la solución oscila salvajemente cerca de algún punto. Tal ejemplo se da en el Proyecto II del IODE. La solución puede existir en todos los puntos, pero incluso un método numérico mucho mejor que Euler necesitaría un tamaño de paso increíblemente pequeño para aproximar la solución con una precisión razonable. Y es posible que las computadoras no puedan manejar fácilmente un tamaño de paso tan pequeño.

En aplicaciones reales no usaríamos un método simple como el de Euler, el método más simple que probablemente se usaría en una aplicación real es el método estándar Runge-Kutta (ver ejercicios). Ese es un método de cuarto orden, es decir, que si reducimos a la mitad el intervalo, el error generalmente baja por un factor de 16 (es de cuarto orden como$\frac{1}{16} = \frac{1}{2} \text{x} \frac{1}{2} \text{x} \frac{1}{2} \text{x} \frac{1}{2}$).

Elegir el método correcto para usar y el tamaño de paso correcto puede ser muy complicado. Hay varios factores que compiten a considerar.

Tiempo computacional: Cada paso lleva tiempo de computadora. Incluso si la función$f$ es sencilla de calcular, la hacemos muchas veces. El tamaño de paso grande significa un cálculo más rápido, pero quizás no la precisión correcta.
Errores de redondez: Las computadoras solo computan con un cierto número de dígitos significativos. Los errores introducidos al redondear números durante nuestros cálculos se notan cuando el tamaño del paso se vuelve demasiado pequeño en relación con las cantidades con las que estamos trabajando. Por lo tanto, reducir el tamaño del paso de hecho puede empeorar los errores.
Estabilidad: Ciertas ecuaciones pueden ser numéricamente inestables. Lo que puede pasar es que los números nunca parecen estabilizarse sin importar cuántas veces redujamos a la mitad el intervalo. Es posible que necesitemos un tamaño de intervalo ridículamente pequeño, lo que puede no ser práctico debido a errores de redondeo o consideraciones de tiempo computacional. Tales problemas a veces se llaman rígidos. En el peor de los casos, los cálculos numéricos podrían estar dándonos números falsos que parecen una respuesta correcta. El hecho de que los números se hayan estabilizado después del halving sucesivo, no significa que debamos tener la respuesta correcta.

Solo hemos visto los inicios de los retos que aparecen en las aplicaciones reales. La aproximación numérica de soluciones a ecuaciones diferenciales es un área de investigación activa para ingenieros y matemáticos. Por ejemplo, el método de propósito general utilizado para el solucionador de ODE en Matlab y Octave (al momento de escribir este artículo) es un método que apareció en la literatura solo en la década de 1980.

Notas al pie

[1] Nombrado así por el matemático suizo Leonhard Paul Euler (1707—1783). La pronunciación correcta del nombre suena más como “engrase”.

Search

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)