2.4: Vibraciones mecánicas
- Page ID
- 115344
Veamos algunas aplicaciones de las ecuaciones lineales de coeficiente constante de segundo orden.
Algunos ejemplos
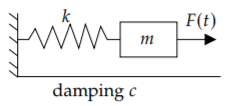
Nuestro primer ejemplo es una masa en un resorte. Supongamos que tenemos una masa\(m > 0 \) (en kilogramos) conectada por un resorte con constante de resorte\( k > 0 \) (en newtons por metro) a una pared fija. Puede haber alguna fuerza externa\( F(t) \) (en newtons) actuando sobre la masa. Finalmente, hay cierta fricción medida por\( c \geq 0 \) (en newton-segundos por metro) a medida que la masa se desliza a lo largo del piso (o tal vez hay un amortiguador conectado).
Dejar\(x\) ser el desplazamiento de la masa (\( x = 0 \)es la posición de reposo), con\(x\) crecimiento hacia la derecha (lejos de la pared). La fuerza ejercida por el resorte es proporcional a la compresión del resorte por la ley de Hooke. Por lo tanto, está\(kx\) en la dirección negativa. De igual manera, la cantidad de fuerza ejercida por la fricción es proporcional a la velocidad de la masa. Por la segunda ley de Newton sabemos que la fuerza es igual a la masa por aceleración y por lo tanto\( mx'' = F(t) - cx' - kx \) o
\[mx'' + cx' + kx = F(t) \nonumber \]
Este es un coeficiente constante lineal de segundo orden ODE. Establecimos alguna terminología sobre esta ecuación. Decimos que la moción es
- forzado, si\( F \not \equiv 0\) (si no\(F\) es idéntico cero),
- no forzado o libre, si\(F \equiv 0 \) (si\(F\) es idéntico cero),
- amortiguado, si\( c > 0 \), y
- sin amortiguar, si\( c = 0 \).
Este sistema aparece en muchas aplicaciones aunque al principio no lo parezca. Muchos escenarios del mundo real se pueden simplificar a una masa en un resorte. Por ejemplo, una configuración de bungee jump es esencialmente un sistema de masa y resorte (tú eres la masa). Sería bueno que alguien hiciera las cuentas antes de saltar del puente, ¿verdad? Demos otros dos ejemplos.
Aquí hay un ejemplo para ingenieros eléctricos. Considera el\(RLC\) circuito en la foto. Hay una resistencia con una resistencia de\(R\) ohmios, un inductor con una inductancia de\(L\) henries, y un condensador con una capacitancia de\(C\) faradios. También hay una fuente eléctrica (como una batería) que da un voltaje de\(E(t)\) voltios a la vez\(t\) (medido en segundos). Dejar\(Q(t)\) ser la carga en culombios en el condensador y\(I(t)\) ser la corriente en el circuito. La relación entre ambos es\(Q' = I\). Por principios elementales encontramos\(L I' + RI + \frac{Q}{C} = E\). Diferenciamos para obtener
\[L I''(t) + R I'(t) + \frac{1}{C} I(t) = E'(t) . \nonumber \]
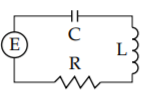
Esta es una ecuación lineal de coeficiente constante de segundo orden no homogénea. Como\(L, R\), y todos\(C\) son positivos, este sistema se comporta igual que el sistema de masa y resorte. La posición de la masa se sustituye por corriente. La masa es reemplazada por inductancia, la amortiguación es reemplazada por resistencia y la constante de resorte se reemplaza por una sobre la capacitancia. El cambio en el voltaje se convierte en la función de forzamiento; para voltaje constante, este es un movimiento no forzado.
Nuestro siguiente ejemplo se comporta como un sistema de masa y resorte solo aproximadamente. Supongamos que una masa\(m\) cuelga de un péndulo de longitud\(L\). Buscamos una ecuación para el ángulo\(\theta(t)\) (en radianes). \(g\)Sea la fuerza de la gravedad. La física elemental exige que la ecuación sea\[\theta'' + \frac{g}{L} \sin \theta = 0 . \nonumber \]
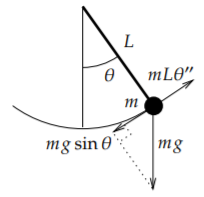
Derivamos esta ecuación usando la segunda ley de Newton: la fuerza es igual a la masa por la aceleración. La aceleración es\(L \theta''\) y la masa es\(m\). Entonces\(mL\theta''\) tiene que ser igual al componente tangencial de la fuerza dada por la gravedad, que está\(m g \sin \theta\) en la dirección opuesta. Entonces\(mL\theta'' = -mg \sin \theta\). El\(m\) curiosamente cancela de la ecuación.
Ahora hacemos nuestra aproximación. Para pequeños\(\theta\) tenemos eso aproximadamente\(\sin \theta \approx \theta\). Esto se puede ver mirando la gráfica. En la Figura\(\PageIndex{4}\) podemos ver que para aproximadamente\(-0.5 < \theta < 0.5\) (en radianes) las gráficas de\(\sin \theta\) y\(\theta\) son casi las mismas.
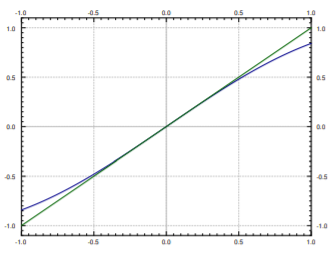
Por lo tanto, cuando los columpios son pequeños,\(\theta\) es pequeño y podemos modelar el comportamiento por la ecuación lineal más simple\[\theta'' + \frac{g}{L} \theta = 0 . \nonumber \]
Los errores de esta aproximación se construyen. Entonces, después de mucho tiempo, el estado del sistema del mundo real podría ser sustancialmente diferente de nuestra solución. También veremos que en un sistema masa-resorte, la amplitud es independiente del periodo. Esto no es cierto para un péndulo. Sin embargo, por periodos de tiempo razonablemente cortos y pequeñas oscilaciones (es decir, solo pequeños ángulos\(\theta\)), la aproximación es razonablemente buena.
En los problemas del mundo real a menudo es necesario hacer este tipo de simplificaciones. Debemos entender tanto las matemáticas como la física de la situación para ver si la simplificación es válida en el contexto de las preguntas que estamos tratando de responder.
Movimiento Libre Sin Amortiguar
En esta sección solo consideraremos el movimiento libre o no forzado, ya que aún no podemos resolver ecuaciones no homogéneas. Empecemos con el movimiento sin amortiguar donde\( c = 0 \). Tenemos la ecuación
\[ mx'' + kx = 0 \nonumber \]
Si dividimos por\( m\) y dejamos\(w_0 = \sqrt { \dfrac {k}{m} } \), entonces podemos escribir la ecuación como
\[ x'' + w^2_0 x = 0 \nonumber \]
La solución general a esta ecuación es
\[ x(t) = A \cos (w_0t) + B \sin (w_0t) \nonumber \]
Por una identidad trigonométrica, tenemos eso para dos constantes diferentes\(C\) y\( \gamma\), tenemos
\[ A \cos (w_0t) + B \sin (w_0t) = C \cos (w_0t - \gamma ) \nonumber \]
No es difícil computar eso\( C = \sqrt { A^2 + B^2 } \) y\( \tan \gamma = \dfrac {B}{A} \). Por lo tanto, dejamos\(C\) y\( \gamma \) seremos nuestras constantes arbitrarias y escribimos\( x(t) = C \cos (w_0t - \gamma )\).
Justificar la identidad anterior y verificar las ecuaciones para\(C\) y\( \gamma\). Pista: Comience con\( \cos (\alpha - \beta ) = \cos ( \alpha) \cos (\beta) + \sin ( \alpha) \sin (\beta) \) y multiplique por\( C\). Entonces piensa lo que debería\( \alpha \) y\( \beta \) ser.
Si bien generalmente es más fácil usar la primera forma con\( A\) y\(B\) resolver las condiciones iniciales, la segunda forma es mucho más natural. Las constantes\(C\) y\( \gamma\) tienen muy buena interpretación. Miramos la forma de la solución
\[ x(t) = C \cos (w_0t - \gamma ) \nonumber \]
Podemos ver que la amplitud es\( C \),\(w_0\) es la frecuencia (angular), y\( \gamma \) es el llamado desplazamiento de fase. El desplazamiento de fase simplemente desplaza la gráfica a la izquierda o a la derecha. Llamamos a\( w_0\) la frecuencia natural (angular). Toda esta configuración se suele llamar movimiento armónico simple.
Hagamos una pausa para explicar la palabra angular antes de la palabra frecuencia. Las unidades de\(w_0\) son radianes por unidad de tiempo, no ciclos por unidad de tiempo como es la medida habitual de frecuencia. Debido a que sabemos que un ciclo es\(2 \pi\) radianes, la frecuencia habitual viene dada por\( \dfrac {w_0}{ 2 \pi} \). Simplemente es cuestión de dónde ponemos la constante\( 2 \pi\), y eso es cuestión de gustos.
El periodo del movimiento es uno sobre la frecuencia (en ciclos por unidad de tiempo) y por lo tanto\( \dfrac {2 \pi}{w_0} \). Esa es la cantidad de tiempo que lleva completar una oscilación completa.
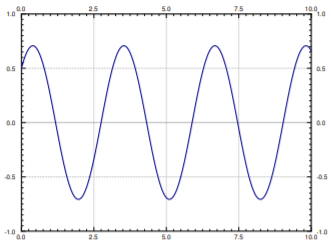
Supongamos que\( m = 2kg \) y\(k = 8 \dfrac {N}{m}\). Toda la masa y la configuración de muelles está sentada en un camión al que viajaba\( 1 \dfrac {m}{s} \). El camión choca y por lo tanto se detiene. La misa se llevó a cabo en su lugar\(0.5\) metros adelante de la posición de descanso. Durante el choque la masa se suelta. Es decir, la masa ahora avanza en\( 1 \dfrac {m}{s} \), mientras que el otro extremo del resorte se mantiene en su lugar. Por lo tanto, la masa comienza a oscilar. Cuál es la frecuencia de la oscilación resultante y cuál es la amplitud. Las unidades son las unidades mks (metros-kilogramos-segundos).
La configuración significa que la masa estaba a medio metro en la dirección positiva durante el choque y con relación a la pared en la que está montado el resorte, la masa se estaba moviendo hacia adelante (en la dirección positiva) en\( 1 \dfrac {m}{s} \). Esto nos da las condiciones iniciales.
Entonces la ecuación con condiciones iniciales es
\[ 2x'' + 8x = 0, \quad x(0) = 0.5,\quad x'(0) = 1 \nonumber \]
Podemos calcular directamente\( w_0 = \sqrt { \dfrac {k}{m} } = \sqrt {4} = 2 \). De ahí que la frecuencia angular sea 2. La frecuencia habitual en Hertz (ciclos por segundo) es\( \dfrac {2}{2 \pi} = \dfrac {1}{ \pi} \approx 0.318 \).
La solución general es
\[ x(t) = A \cos (2t) + B \sin (2t) \nonumber \]
Dejar\( x(0) = 0.5 \) significa\(A = 0.5 \). Entonces\(x'(t) = -2(0.5) \sin (2t) + 2B \cos (2t) \). Dejando\( x'(0) = 1\) que lleguemos\(B = 0.5\). Por lo tanto, la amplitud es\( C = \sqrt { A^2 + B^2} = \sqrt { 0.25 + 0.25 } = \sqrt {0.5} \approx 0.707\). La solución es
\[ x(t) = 0.5 \cos (2t) + 0.5 \sin (2t) \nonumber \]
Una gráfica de\( x(t) \) se muestra en la Figura\(\PageIndex{5}\).
En general, para el movimiento libre sin amortiguar, una solución de la forma
\[ x(t) = A \cos (w_0t) + B \sin (w_0t) \nonumber \]
corresponde a las condiciones iniciales\( x(0) = A \) y\(x'(0) = w_0B\). Por lo tanto, es fácil de entender\(A\) y a\(B\) partir de las condiciones iniciales. La amplitud y el desplazamiento de fase se pueden calcular a partir de\(A\) y\(B\). En el ejemplo, ya encontramos la amplitud\(C\). Calculemos el desplazamiento de fase. Eso lo sabemos\( \tan \gamma = \dfrac {B}{A} = 1\). Tomamos el arcoangente de 1 y obtenemos aproximadamente 0.785. Todavía necesitamos verificar si esto\( \gamma\) está en el cuadrante correcto (y agregar\( \pi\) a\( \gamma\) si no lo está). Dado que ambos\(A\) y\(B\) son positivos, entonces\( \gamma\) debería estar en el primer cuadrante, y 0.785 radianes realmente está en el primer cuadrante.
Muchas calculadoras y programas informáticos no sólo tienen la función atan para arctangent, sino también lo que a veces se llama atan2. Esta función toma dos argumentos,\(B\) y\(A\), y devuelve a\( \gamma\) en el cuadrante correcto para usted.
Movimiento Libre Damped
Centrémonos ahora en el movimiento amortiguado. Reescribamos la ecuación
\[ mx'' + cx' + kx = 0 \nonumber \]
como
\[ x'' + 2px' + w^2_0x = 0 \nonumber \]
donde
\[ w_0 = \sqrt {\dfrac {k}{m}},\quad p = \dfrac {c}{2m} \nonumber \]
La ecuación característica es
\[ r^2 + 2pr + w^2_0 = 0 \nonumber \]
Usando la fórmula cuadrática obtenemos que las raíces son
\[ r = -p \pm \sqrt { p^2 - w^2_0} \nonumber \]
La forma de la solución depende de si obtenemos raíces complejas o reales. Obtenemos raíces reales si y solo si el siguiente número no es negativo:
\[ p^2 - w^2_0 = { ( \dfrac {c}{2m} )}^2 - \dfrac {k}{m} = \dfrac {c^2 -4km}{4m^2} \nonumber \]
El signo de\( p^2 - w^2_0 \) es lo mismo que el signo de\(c^2 - 4km\). Así obtenemos raíces reales si y solo si\( c^2 - 4km \) es no negativo, o en otras palabras si\( c^2 \ge 4km \).
Sobre-amortiguación
Cuando\( c^2 - 4km > 0\), decimos que el sistema está sobreamortiguado. En este caso, hay dos raíces reales distintas\(r_1\) y\(r_2\). Observe que ambas raíces son negativas. Como siempre\( \sqrt {p^2 - w^2_0} \) es menor que\(P\), entonces\( -P \pm \sqrt {P^2 - w^2_0}\) es negativo.
La solución es\[ x(t) = C_1e^{r_1t} + C_2e^{r_2t} \nonumber \]
Ya que\(r_1, r_2\) son negativos,\( x(t) \rightarrow 0 \) como\(t \rightarrow \infty\). Así la masa tenderá hacia la posición de descanso a medida que el tiempo va hasta el infinito. Para algunas parcelas de muestra para diferentes condiciones iniciales (Figura\(\PageIndex{6}\)).
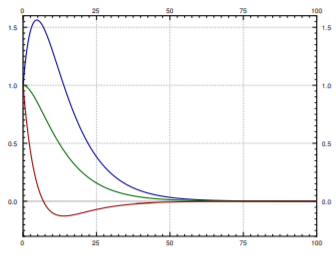
Tenga en cuenta que no ocurre ninguna oscilación. De hecho, la gráfica cruzará el\(x\) eje como máximo una vez. Para ver por qué, tratamos de resolver\(0 = C_1e^{r_1t} + C_2e^{r_2t} \). Por lo tanto,\( C_1e^{r_1t} = -C_2e^{r_2t} \) y usando leyes de exponentes obtenemos
\[ \dfrac {-C_1}{C_2} = e^{{(r_2 - r_1)}t} \nonumber \]
Esta ecuación tiene como máximo una solución\(t \ge 0\). Para algunas condiciones iniciales la gráfica nunca cruzará el\(x\) eje, como es evidente a partir de las gráficas de muestra.
Supongamos que la masa se libera del descanso. Eso es\( x(0) = x_0 \) y\(x'(0) = 0 \). Entonces
\[ x(t) = \dfrac {x_0}{r_1 - r_2} (r_1e^{r_2t} - r_2e^{r_1t}) \nonumber \]
No es difícil ver que esto satisface las condiciones iniciales.
Amortiguación crítica
Cuando\( c^2 - 4km = 0 \), decimos que el sistema está críticamente amortiguado. En este caso, hay una raíz de multiplicidad 2 y esta raíz es\( -P\). Por lo tanto, nuestra solución es
\[ x(t) = C_1e^{-pt} + C_2te^{-pt} \nonumber \]
El comportamiento de un sistema de amortiguamiento crítico es muy similar al de un sistema sobreamortiguado. Después de todo, un sistema críticamente amortiguado es en cierto sentido un límite de sistemas sobreamortiguados. Dado que estas ecuaciones son realmente solo una aproximación al mundo real, en realidad nunca estamos amortiguados críticamente, es un lugar al que solo podemos llegar en teoría. Siempre estamos un poco poco amortiguados o un poco sobrehumedecidos. Es mejor no detenerse en la amortiguación crítica.
Subamortiguamiento
Cuando\( c^2 - 4km < 0 \), decimos que el sistema está subamortiguado. En este caso, las raíces son complejas.
\[\begin{align}\begin{aligned} r &= -p \pm \sqrt { p^2 - w^2_0} \\ &= -p \pm \sqrt {-1} \sqrt {w^2_0 - p^2} \\ & = -p \pm iw_1 \end{aligned}\end{align} \nonumber \]
donde\( w_1 = \sqrt { w^2_0 - p^2 } \). Nuestra solución es
\[ x(t) = e^{-pt} ( A \cos (w_1t) + B \sin (w_1t) \nonumber \]
o
\[ x(t) = Ce^{-pt} \cos ( w_1t - \gamma) \nonumber \]
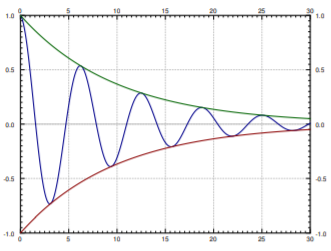
Una gráfica de ejemplo se da en la Figura\(\PageIndex{7}\). Tenga en cuenta que todavía tenemos eso\( x(t) \rightarrow 0 \) como\( t \rightarrow \infty \).
En la figura también mostramos las curvas de envolvente\( Ce^{-pt} \) y\( - Ce^{pt} \). La solución es la línea oscilante entre las dos curvas de envolvente. Las curvas de envolvente dan la amplitud máxima de la oscilación en cualquier punto dado en el tiempo. Por ejemplo, si eres puenting, estás realmente interesado en computar la curva envolvente para que no golpees el concreto con la cabeza.
El desplazamiento de fase\( \gamma\) simplemente desplaza la gráfica a la izquierda o a la derecha pero dentro de las curvas de envolvente (las curvas de envolvente no cambian si\( \gamma\) cambian).
Por último, tenga en cuenta que la pseudo-frecuencia angular \(^{1}\)(no la llamamos frecuencia ya que la solución no es realmente una función periódica)\(w_1\) se vuelve más pequeña cuando la amortiguación\(c\) (y por lo tanto\(P\)) se hace mayor. Esto tiene sentido. Cuando cambiamos el amortiguamiento un poco, no esperamos que el comportamiento de la solución cambie drásticamente. Si seguimos haciendo\(c\) más grandes, entonces en algún momento la solución debería comenzar a parecerse a la solución para amortiguación crítica o sobreamortiguación, donde no ocurre ninguna oscilación. Entonces si\(c^2\) se acerca\(4km\), queremos acercarnos\(w_1\) a 0.
Por otro lado, cuando\(c\) se hace más pequeño, se\(w_1\) acerca\(w_0\) (siempre\(w_1\) es más pequeño que\(w_0\)), y la solución se parece cada vez más al movimiento periódico constante de la caja sin amortiguar. Las curvas de envolvente se vuelven más planas y planas a medida que\(c\) (y por lo tanto\(P\)) va a 0.
Notas al pie
[1] No llamamos a\(\omega_{1}\) una frecuencia ya que la solución no es realmente una función periódica.


