3.1: Introducción a los Sistemas de ODEs
- Page ID
- 115420
Muchas veces no tenemos una sola variable dependiente y solo una ecuación diferencial, podemos terminar con sistemas de varias ecuaciones y varias variables dependientes aunque empecemos con una sola ecuación.
Si tenemos varias variables dependientes, supongamos\(y_1\),\(y_2\),...\(y_n\), entonces podemos tener una ecuación diferencial que involucre a todas ellas y sus derivadas. Por ejemplo,\( y''_1= f(y'_1,y'_2,y_1,y_2,x)\). Por lo general, cuando tenemos dos variables dependientes tenemos dos ecuaciones como
\[\begin{align}\begin{aligned} y''_1&= f_1(y'_1,y'_2,y_1,y_2,x)\\ y''_2&= f_2(y'_1,y'_2,y_1,y_2,x)\end{aligned}\end{align} \nonumber \]
para algunas funciones\(f_1\) y\(f_2\). Llamamos a lo anterior un sistema de ecuaciones diferenciales. Más precisamente, lo anterior es un sistema de segundo orden de ODEs como aparecen derivados de segundo orden. El sistema\[\begin{align}\begin{aligned} x_1' & = g_1(x_1,x_2,x_3,t) , \\ x_2' & = g_2(x_1,x_2,x_3,t) , \\ x_3' & = g_3(x_1,x_2,x_3,t) ,\end{aligned}\end{align} \nonumber \] es un sistema de primer orden, donde\(x_1,x_2,x_3\) están las variables dependientes, y\(t\) es la variable independiente.
La terminología para los sistemas es esencialmente la misma que para las ecuaciones simples. Para el sistema anterior, una solución es un conjunto de tres funciones\(x_1(t)\),\(x_2(t)\),\(x_3(t)\), tal que\[\begin{align}\begin{aligned} x_1'(t) &= g_1\bigl(x_1(t),x_2(t),x_3(t),t\bigr) , \\ x_2'(t) &= g_2\bigl(x_1(t),x_2(t),x_3(t),t\bigr) , \\ x_3'(t) &= g_3\bigl(x_1(t),x_2(t),x_3(t),t\bigr) .\end{aligned}\end{align} \nonumber \]
Por lo general, también tenemos una condición inicial. Al igual que para las ecuaciones simples especificamos\(x_1\)\(x_2\),, y\(x_3\) para algunas fijas\(t\). Por ejemplo,\(x_1(0) = a_1\),\(x_2(0) = a_2\),\(x_3(0) = a_3\). Para algunas constantes\(a_1\),\(a_2\), y\(a_3\). Para el sistema de segundo orden especificaríamos también las primeras derivadas en un punto. Y si encontramos una solución con constantes en ella, donde resolviendo para las constantes encontramos una solución para cualquier condición inicial, llamamos a esta solución la solución general. Lo mejor es mirar un ejemplo sencillo.
A veces un sistema es fácil de resolver resolviendo para una variable y luego para la segunda variable. Toma el sistema de primer pedido
\[\begin{align} \begin{aligned} y'_1 &= y_1, \\ y'_2 &= y_1 - y_2,\end{aligned}\end{align} \nonumber \]
con condiciones iniciales de la forma\(y_1(0) = 1\) y\(y_2(0) = 2\).
Solución
Observamos que\( y_1 = C_1e^x\) es la solución general de la primera ecuación. Luego enchufamos esto\(y_1\) en la segunda ecuación y obtenemos la ecuación\(y'_2=C_1e^x-y_2\), que es una ecuación lineal de primer orden que se resuelve fácilmente para\(y_2\). Por el método de integración del factor obtenemos
\[ e^xy_2 = \dfrac{C_1}{2}e^{2x} + C_2 \nonumber \]o\[ y_2 = \dfrac{C_1}{2}e^2 + C_2 e^{-x}. \nonumber \]
La solución general al sistema es, por lo tanto,
\[ y_1 = C_1e^e,\quad\text{and}\quad y_2 = \dfrac{C_1}{2}e^x + C_2e^{-x}. \nonumber \]
Ahora resolvemos por\(C_1\) y\(C_2\) dadas las condiciones iniciales. Nosotros sustituimos\(x=0\) y encontramos eso\(C_1 =1\) y\(C_2 =\frac{3}{2}\). Así la solución es:\(y_1 = e^x,\) y\( y_2 = \dfrac{1}{2}e^x + \dfrac{3}{2}e^{-x}\).
Generalmente, no tendremos tanta suerte de poder resolver para cada variable por separado como en el ejemplo anterior, y tendremos que resolver para todas las variables a la vez. Si bien generalmente no podremos resolver para una variable y luego la siguiente, intentaremos rescatar lo más posible de esta técnica. Resultará que en cierto sentido todavía (intentaremos) resolver un montón de ecuaciones individuales y juntar sus soluciones. No nos preocupemos ahora mismo de cómo resolver sistemas todavía.
Consideraremos principalmente los sistemas lineales. El ejemplo anterior es un llamado sistema lineal de primer orden. Es lineal ya que ninguna de las variables dependientes o sus derivadas aparecen en funciones no lineales o con potencias superiores a una (\(x\)\(y\),,\(x'\) y\(y'\), constantes, y funciones de\(t\) pueden aparecer, pero no\(xy\) o\({(y')}^2\) o\(x^3\)). Otro ejemplo, más complicado, de un sistema lineal es\[\begin{align}\begin{aligned} y_1'' &= e^t y_1' + t^2 y_1 + 5 y_2 + \sin(t), \\ y_2'' &= t y_1'-y_2' + 2 y_1 + \cos(t).\end{aligned}\end{align} \nonumber \]
Aplicaciones
Consideremos algunas aplicaciones simples de los sistemas y cómo configurar las ecuaciones.
Primero, consideramos los tanques de sal y salmuera, pero esta vez el agua fluye de uno a otro y viceversa. De nuevo consideramos que los tanques están mezclados de manera uniforme.
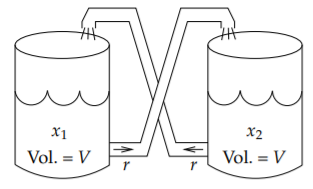
Supongamos que tenemos dos tanques, cada uno conteniendo\(V\) litros de volumen de salmuera salina. La cantidad de sal en el primer tanque es de\(x_1\) gramos, y la cantidad de sal en el segundo tanque es de\(x_2\) gramos. El líquido se mezcla perfectamente y fluye a la velocidad\(r\) litros por segundo fuera de cada tanque hacia el otro. Ver Figura\(\PageIndex{1}\).
La tasa de cambio de\(x_1\), es decir\(x_1'\), es la tasa de sal que entra menos la tasa que sale. La tasa que entra es la densidad de la sal en el tanque 2, es decir\(\frac{x_2}{V}\), multiplicada por la tasa\(r\). La tasa que sale es la densidad de la sal en el tanque 1, es decir\(\frac{x_1}{V}\), multiplicada por la tasa\(r\). En otras palabras es\[x_1' = \frac{x_2}{V} r - \frac{x_1}{V} r = \frac{r}{V} x_2 - \frac{r}{V} x_1 = \frac{r}{V} (x_2-x_1). \nonumber \] De igual manera encontramos la tasa\(x_2'\), donde los roles de\(x_1\) y\(x_2\) se invierten. Con todo, el sistema de ODEs para este problema es\[\begin{align}\begin{aligned} x_1' & = \frac{r}{V} (x_2-x_1), \\ x_2' & = \frac{r}{V} (x_1-x_2).\end{aligned}\end{align} \nonumber \] En este sistema no podemos resolver por\(x_1\) o\(x_2\) por separado. Debemos resolver para ambos\(x_1\) y\(x_2\) a la vez, lo cual es intuitivamente claro ya que la cantidad de sal en un tanque afecta la cantidad en el otro. No podemos saber\(x_1\) antes de saberlo\(x_2\), y viceversa.
Todavía no sabemos cómo encontrar todas las soluciones, pero intuitivamente podemos al menos encontrar algunas soluciones. Supongamos que sabemos que inicialmente los tanques tienen la misma cantidad de sal. Es decir, tenemos una condición inicial como\(x_1(0)=x_2(0) = C\). Entonces claramente la cantidad de sal que sale y sale de cada tanque es la misma, por lo que las cantidades no van cambiando. En otras palabras,\(x_1 = C\) y\(x_2 = C\) (las funciones constantes) es una solución:\(x_1' = x_2' = 0\), y\(x_2-x_1 = x_1-x_2 = 0\), así se satisfacen las ecuaciones.
Pensemos un poco más en la configuración sin resolverla. Supongamos que las condiciones iniciales son\(x_1(0) = A\) y\(x_2(0) = B\), para dos constantes diferentes\(A\) y\(B\). Dado que no entra ni sale sal de este sistema cerrado, la cantidad total de sal es constante. Es decir,\(x_1+x_2\) es constante, y así es igual\(A+B\). Intuitivamente si\(A\) es más grande que\(B\), entonces fluirá más sal del tanque uno que hacia él. Eventualmente, después de mucho tiempo esperaríamos entonces que la cantidad de sal en cada tanque se igualara. En otras palabras, las soluciones de ambos\(x_1\) y\(x_2\) deben tender hacia\(\frac{A+B}{2}\). Una vez que sepas cómo resolver sistemas te darás cuenta de que esto realmente es así.
Como aplicación de ejemplo, volvamos a pensar en los sistemas de masa y muelles.
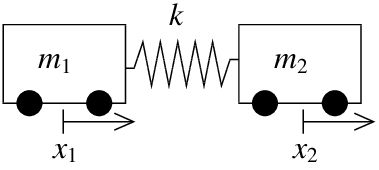
Como aplicación de ejemplo, volvamos a pensar en los sistemas de masa y muelles. Supongamos que tenemos un resorte con constante\(k\), pero dos masas\(m_1\) y\(m_2\). Podemos pensar en las masas como carros, y supondremos que van por una vía recta sin fricción. Dejar\(x_1\) ser el desplazamiento del primer carro y\(x_2\) ser el desplazamiento del segundo carro. Es decir, colocamos los dos carros en algún lugar sin tensión en el muelle, y marcamos la posición del primer y segundo carro y llamamos a esos las posiciones cero. Luego\(x_1\) mide qué tan lejos está el primer carro de su posición cero, y\(x_2\) mide qué tan lejos está el segundo carro de su posición cero. La fuerza ejercida por el muelle sobre el primer carro es\( k(x_2 - x_1)\), ya que\(x_2-x_1\) es lo lejos que se estira (o comprime) la cuerda de la posición de reposo. La fuerza ejercida sobre el segundo carro es lo contrario, por lo tanto lo mismo con un signo negativo.
La segunda ley de Newton establece que la fuerza es igual a la masa por aceleración. Entonces el sistema de ecuaciones que gobierna la configuración es
\[\begin{align}\begin{aligned} m_1x''_1 &= k(x_2 - x_1) \\ m_2x''_2&= -k(x_2 - x_1) \end{aligned}\end{align} \nonumber \]
En este sistema no podemos resolver para la\(x_2\) variable\(x_1\) o por separado. Eso debemos resolver para ambos\(x_1\) y\(x_2\) a la vez es intuitivamente claro, ya que a dónde va el primer carro depende exactamente de donde vaya el segundo carro y viceversa.
Cambiando a Primer Orden
Antes de hablar de cómo manejar los sistemas, señalemos que en algún sentido solo necesitamos considerar sistemas de primer orden. Tomemos una ecuación diferencial de\(n^{th}\) orden
\[ y^{(n)} = F(y^{(n-1)}, ..., y', y, x ). \nonumber \]
Definimos nuevas variables\(u_1, ..., u_n\) y escribimos el sistema
\[\begin{align}\begin{aligned} u'_1 &= u_2 \\ u'_2 &= u_3 \\ &\vdots \\ u'_{n-1} &= u_n \\ u'_n &= F(u_n, u_{n-1}, \dots , u_2, u_1, x)\end{aligned}\end{align} \nonumber \]
Resolvemos este sistema para\(u_1, u_2, \dots , u_n\). Una vez que hayamos resuelto para los\(u\)'s, podemos\(u_2\) descartarlos\(u_n\) y dejar\(y=u_1\). Observamos que esto\(y\) resuelve la ecuación original.
Tomar\(x''' = 2x''+ 8x' + x + t\). Dejando\(u_1 = x\)\(u_2 = x'\),\(u_3 = x''\),, encontramos el sistema:\[u_1' = u_2, \qquad u_2' = u_3, \qquad u_3' = 2u_3 + 8u_2 + u_1 + t . \nonumber \]
Un proceso similar se puede seguir para un sistema de ecuaciones diferenciales de orden superior. Por ejemplo, un sistema de ecuaciones\(k\) diferenciales en\(k\) incógnitas, todas de orden\(n\), puede transformarse en un sistema de\(n \times k\) ecuaciones e\(n \times k\) incógnitas de primer orden.
Consideremos el sistema a partir de los carritos ejemplo,\[m_1 x_1'' = k(x_2-x_1), \qquad m_2 x_2'' = - k(x_2-x_1) . \nonumber \] Let\(u_1 = x_1\)\(u_2 = x_1'\),,\(u_3 = x_2\),\(u_4 = x_2'\). El sistema de segundo orden se convierte en el sistema de primer orden\[u_1' = u_2, \qquad m_1 u_2' = k(u_3-u_1), \qquad u_3' = u_4, \qquad m_2 u_4' = - k(u_3-u_1) . \nonumber \]
A veces también podemos usar esta idea a la inversa. Tomemos el sistema
\[ x' = 2y-x, \quad y'=x, \nonumber \]
donde está la variable independiente\(t\). Deseamos resolver por las condiciones iniciales\(x(0)=1\) y\(y(0)=0\).
Si diferenciamos la segunda ecuación que obtenemos\(y''=x'\). Sabemos lo que\(x'\) es en términos de\(x\) y\(y\), y eso lo sabemos\(x=y'\).
\[ y''=x'=2y-x=2y-y'. \nonumber \]
Ahora tenemos la ecuación\( y'' + y' - 2y = 0 \). Sabemos resolver esta ecuación y la encontramos\( y = C_1e^{-2t} + C_2e^t \). Una vez que\(y\) tenemos usamos la ecuación\( y' = x\) para obtener\(x\).
\[ x = y' = -2C_1e^{-2t} + C_2e^t \nonumber \]
Resolvemos para las condiciones iniciales\( 1 = x(0) = -2C_1 + C_2 \) y\( 0 = y(0) = C_1 + C_2 \). De ahí,\( C_1 = - C_2\) y\( 1 = 3C_2\). Entonces\( C_1 = -\frac {1}{3} \) y\( C_2 = \frac {1}{3} \). Nuestra solución es
\[ x = \frac {2e^{-2t} + e^t}{3}, \quad y = \frac {-e^{-2t} + e^t}{3} \nonumber \]
Conéctate y confirma que esta es realmente la solución.
Es útil ir y venir entre sistemas y ecuaciones de orden superior por otras razones. Por ejemplo, el software para resolver ODE numéricamente (aproximación) es generalmente para sistemas de primer orden. Para usarlo, tomas cualquier ODE que quieras resolver y convertirla en un sistema de primer orden. No es muy difícil adaptar el código de computadora para el método Euler o Runge—Kutta para ecuaciones de primer orden para manejar sistemas de primer orden. Simplemente tratamos la variable dependiente no como un número sino como un vector. En muchos lenguajes matemáticos de computación casi no hay distinción en la sintaxis.
Sistemas Autónomos y Campos Vectoriales
Un sistema donde las ecuaciones no dependen de la variable independiente se denomina sistema autónomo. Por ejemplo el sistema\(y'=2y-x\),\(y'=x\) es autónomo como lo\(t\) es la variable independiente pero no aparece en las ecuaciones.
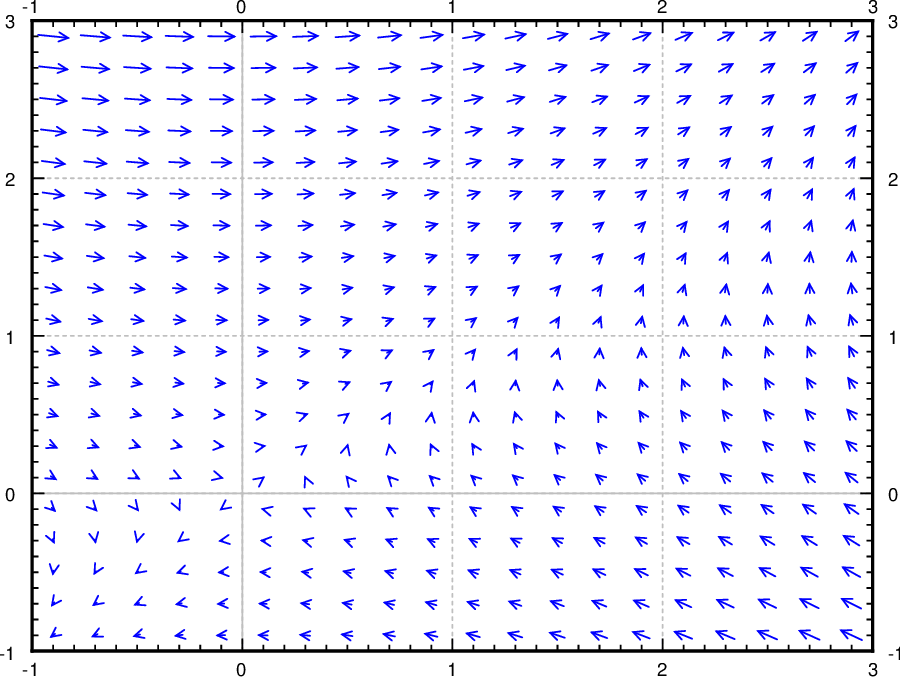
Para sistemas autónomos podemos dibujar el llamado campo de dirección o campo vectorial, una parcela similar a un campo de pendiente, pero en lugar de dar una pendiente en cada punto, damos una dirección (y una magnitud). El ejemplo anterior,\(x' = 2y-x\),\(y' = x\), dice que en el punto\((x,y)\) la dirección en la que debemos viajar para satisfacer las ecuaciones debe ser la dirección del vector\(( 2y-x, x )\) con la velocidad igual a la magnitud de este vector. Entonces dibujamos el vector\((2y-x,x)\) en el punto\((x,y)\) y lo hacemos por muchos puntos en el\(xy\) plano -. Por ejemplo, en el punto\((1,2)\) dibujamos el vector\(\bigl(2(2)-1,1\bigr) = (3,1)\), un vector apuntando a la derecha y un poco hacia arriba, mientras que en el punto\((2,1)\) dibujamos el vector\(\bigl(2(1)-2,2\bigr) = (0,2)\) un vector que apunta hacia arriba. Al dibujar los vectores, vamos a reducir su tamaño para que se ajusten a muchos de ellos en el mismo campo de dirección. Si dibujamos las flechas al tamaño real, el diagrama sería un desastre desordenado una vez que dibujarías más de un par de flechas. Entonces los escalamos a todos para que ni siquiera el más largo interfiera con los demás. Estamos mayormente interesados en su dirección y tamaño relativo. Ver Figura\(\PageIndex{3}\).
Podemos trazar un camino de la solución en el plano. Supongamos que la solución viene dada por\(x = f(t)\),\(y=g(t)\). Escogemos un intervalo de\(t\) (digamos\(0 \leq t \leq 2\) para nuestro ejemplo) y trazamos todos los puntos\(\bigl(f(t),g(t)\bigr)\) para\(t\) en el rango seleccionado. La imagen resultante se llama retrato de fase (o retrato plano de fase). La curva particular obtenida se denomina trayectoria o curva de solución. Ver una gráfica de ejemplo en la Figura\(\PageIndex{4}\). En la figura la solución comienza en\((1,0)\) y viaja a lo largo del campo vectorial por una distancia de 2 unidades de\(t\). Resolvimos este sistema precisamente, así que calculamos\(x(2)\) y\(y(2)\) para encontrar\(x(2) \approx 2.475\) y\(y(2) \approx 2.457\). Este punto corresponde al extremo superior derecho de la curva de solución trazada en la figura.
Observe la similitud con los diagramas que dibujamos para sistemas autónomos en una dimensión. Pero tenga en cuenta lo mucho más complicadas que se vuelven las cosas cuando permitimos solo una dimensión extra.
Podemos dibujar retratos de fase y trayectorias en el\(xy\) plano aunque el sistema no sea autónomo. En este caso, sin embargo, no podemos dibujar el campo de dirección, ya que el campo cambia a medida que\(t\) cambia. Para cada uno\(t\) obtendríamos un campo de dirección diferente.

Teorema de Picard
Quizás antes de ir más allá, mencionemos que el teorema de Picard sobre la existencia y la singularidad aún se mantiene para los sistemas de ODE. Replanteemos este teorema en el marco de los sistemas. Un sistema general de primer orden es de la forma\[ \begin{align} \begin{aligned} x_1' & = F_1(x_1,x_2,\ldots,x_n,t) , \\ x_2' & = F_2(x_1,x_2,\ldots,x_n,t) , \\ & \vdots \\ x_n' & = F_n(x_1,x_2,\ldots,x_n,t) . \end{aligned}\end{align} \label{eq:1} \]
Teorema de Picard sobre la existencia y singularidad para los sistemas
Si por todos\(j=1,2,\ldots,n\) y\(k = 1,2,\ldots,n\) cada uno\(F_j\) es continuo y la derivada\(\frac{\partial F_j}{\partial x_k}\) existe y es continua cerca de algunos\((x_1^0,x_2^0,\ldots,x_n^0,t^0)\), entonces una solución a (3.1.21) sujeta a la condición inicial\(x_1(t^0) = x_1^0\),\(x_2(t^0) = x_2^0\),...,\(x_n(t^0) = x_n^0\) existe (al menos para\(t\) en algún pequeño intervalo ) y es único.
Es decir, existe una solución única para cualquier condición inicial dado que el sistema es razonable (\(F_j\)y sus derivadas parciales en las\(x\) variables son continuas). En cuanto a las ecuaciones individuales puede que no tengamos una solución para todos los tiempos\(t\), pero al menos por algún corto periodo de tiempo.
Como podemos cambiar cualquier ODE de orden\(n\) th en un sistema de primer orden, entonces notamos que este teorema proporciona también la existencia y singularidad de soluciones para ecuaciones de orden superior que hasta ahora no hemos declarado explícitamente.


