5.1: Problemas de Sturm-Liouville

Problemas de Valor Límite

En el Capítulo 4 nos hemos encontrado con varios problemas de valor propio diferentes, tales como:

\[ X''(x)+ \lambda X(x)=0 \nonumber \]

con diferentes condiciones de contorno

\[\begin{array}{rrl} X(0) = 0 & ~~X(L) = 0 & ~~\text{(Dirichlet), or} \\ X'(0) = 0 & ~~X'(L) = 0 & ~~\text{(Neumann), or} \\ X'(0) = 0 & ~~X(L) = 0 & ~~\text{(Mixed), or} \\ X(0) = 0 & ~~X'(L) = 0 & ~~\text{(Mixed)}, \ldots \end{array} \nonumber \]

Por ejemplo para el alambre aislado, las condiciones de Dirichlet corresponden a aplicar una temperatura cero en los extremos, Neumann significa aislar los extremos, etc... Otros tipos de condiciones de punto final también surgen naturalmente, como las condiciones de límite Robin

\[hX(0)-X'(0)=0\quad hX(L)+X'(L)=0, \nonumber \]

para alguna constante\(h\). Estas condiciones surgen cuando los extremos se sumergen en algún medio.

Los problemas de límites surgieron en el estudio de la ecuación de calor\(u_t=ku_{xx}\) cuando intentábamos resolver la ecuación por el método de separación de variables en la Sección 4.6. En el cómputo encontramos un cierto problema de valor propio y encontramos las funciones propias\(X_n(x)\). Luego encontramos la descomposición de la función propia de la temperatura inicial\(f(x)=u(x,0)\) en términos de las funciones propias

\[f(x)= \sum_{n=1}^{\infty}c_nX_n(x). \nonumber \]

Una vez que tuvimos esta descomposición y encontramos adecuada\(T_n(t)\) tal que\(T_n(0)=1\) y\(T_n(t)X(x)\) fueron soluciones, la solución al problema original incluyendo la condición inicial podría escribirse como

\[u(x,t)= \sum_{n=1}^{\infty}c_nT_n(t)X_n(x). \nonumber \]

Intentaremos resolver problemas más generales utilizando este método. Primero, estudiaremos ecuaciones lineales de segundo orden de la forma

\[\label{eq:6} \frac{d}{dx}\left( p(x)\frac{dy}{dx} \right)-q(x)y+\lambda r(x)y=0. \]

Esencialmente, cualquier ecuación lineal de segundo orden de la forma\(a(x)y''+b(x)y'+c(x)y+\lambda d(x)y=0\) puede escribirse como\(\eqref{eq:6}\) después de multiplicar por un factor apropiado.

Ejemplo\(\PageIndex{1}\): Sturm-Liouville Problem

Ponga la siguiente ecuación en la forma\(\eqref{eq:6}\):

\[x^2y''+xy'+(\lambda x^2-n^2)y=0. \nonumber \]

Multiplica ambos lados por\( \frac{1}{x}\) para obtener

\[\begin{align}\begin{aligned} \frac{1}{x}(x^2y''+xy'+(\lambda x^2-n^2)y) &=xy''+y'+ \left( \lambda x -\frac{n^2}{x}\right)y &= \frac{d}{dx}\left( x \frac{dy}{dx} \right)-\frac{n^2}{x}y+\lambda xy=0.\end{aligned}\end{align} \nonumber \]

La ecuación de Bessel aparece por ejemplo en la solución de la ecuación de onda bidimensional. Si quieres ver cómo se resuelve la ecuación, puedes mirar la subsección 7.3.3.

El llamado problema de Sturm-Liouville \(^{1}\)es buscar soluciones no triviales para

\[\begin{align}\begin{aligned} \frac{d}{dx}\left( p(x)\frac{dy}{dx} \right)-q(x)y+\lambda r(x)y & =0,~~~~~a<x<b, \\ \alpha_1y(a)-\alpha_2y'(a) &=0, \\ \beta_1y(b)+\beta_2y'(b) &=0.\end{aligned}\end{align} \nonumber \]

En particular, buscamos\(\lambda\) s que permitan soluciones no triviales. Los\(\lambda\) s que admiten soluciones no triviales se denominan valores propios y las soluciones no triviales correspondientes se denominan funciones propias. Las constantes\(\alpha_1\) y no\(\alpha_2\) deben ser tanto cero, igual para\(\beta_1\) y\(\beta_2\).

Teorema\(\PageIndex{1}\)

Supongamos\(p(x),\: p'(x),\: q(x)\) y\(r(x)\) son continuos sobre\([a,b]\) y supongamos\(p(x)>0\) y\(r(x)>0\) para todos\(x\) adentro\([a,b]\). Entonces el problema de Sturm-Liouville (5.1.8) tiene una secuencia creciente de valores propios

\[\lambda_1<\lambda_2<\lambda_3< \cdots \nonumber \]

de tal manera que

\[\lim_{n \rightarrow \infty} \lambda_n= +\infty \nonumber \]

y tal que a cada uno\(\lambda_n\) hay (hasta un múltiplo constante) una sola función propia\(y_n(x)\).

Además, si\(q(x) \geq 0\) y\(\alpha_1, \alpha_2,\beta_1, \beta_2 \geq 0\), entonces\(\lambda_n \geq 0\) para todos\(n\).

Los problemas que satisfacen la hipótesis del teorema (incluyendo el “Además”) se denominan problemas regulares de Sturm-Liouville, y aquí solo consideraremos tales problemas. Es decir, un problema regular es aquel donde\(p(x),\: p'(x),\: q(x)\) y\(r(x)\) son continuos,\(p(x)>0\),\(r(x)>0\),\(q(x) \geq 0\), y\(\alpha_1, \alpha_2,\beta_1, \beta_2 \geq 0\). Nota: Tenga cuidado con las señales. También tenga cuidado con las desigualdades para\(r\) y\(p\), deben ser estrictas para todos\(x\) en el intervalo\([a,b]\), ¡incluyendo los puntos finales!

Cuando cero es un valor propio, generalmente comenzamos a etiquetar los valores propios en\(0\) lugar de en\(1\) por conveniencia. Es decir etiquetamos los valores propios\(\lambda_{0} <\lambda_{1} <\lambda_{2} <\cdots\).

Ejemplo\(\PageIndex{2}\)

El problema\(y''+ \lambda y,\: 0<x<L,\: y(0)=0\), y\(y(L)=0\) es un problema regular de Sturm-Liouville:\(p(x)=1,\: q(x)=0,\: r(x)=1\), y tenemos\(p(x)1>0\) y\(r(x)1>0\). También tenemos\(a=0\),\(b=L\),\(\alpha_{1}=\beta_{1}=1\),\(\alpha_{2}=\beta_{2}=0\). Los valores propios son\(\lambda_n=\frac{n^2 \pi^2}{L^2}\) y las funciones propias son\(y_n(x)=\sin(\frac{n \pi}{L}x)\). Todos los valores propios son no negativos según lo predicho por el teorema.

Ejercicio\(\PageIndex{1}\)

Buscar valores propios y funciones propias para

\[y''+\lambda y=0,~~~~~y'(0)=0,~~~~~y'(1)=0. \nonumber \]

Identificar el\(p,\: q,\: r,\: \alpha_j,\: \beta_j\). ¿Se puede utilizar el teorema para facilitar la búsqueda de valores propios? (Pista: Considere la condición\(-y'(0)=0\))

Ejemplo\(\PageIndex{3}\)

Encontrar valores propios y funciones propias del problema

\[\begin{align}\begin{aligned} y''+\lambda y &=0, & 0<x<1, \\ hy(0)-y'(0) & =0, & y'(1)=0, &\quad h>0.\end{aligned}\end{align} \nonumber \]

Estas ecuaciones dan un problema regular de Sturm-Liouville.

Ejercicio\(\PageIndex{2}\)

Identificar\(p,\: q,\: r,\: \alpha_j,\: \beta_j\) en el ejemplo anterior.

En primer lugar señalar que\(\lambda \geq 0\) por Teorema\(\PageIndex{1}\). Por lo tanto, la solución general (sin condiciones de límite) es

\[\begin{align}\begin{aligned} & y(x) = A \cos ( \sqrt{\lambda}\, x) + B \sin ( \sqrt{\lambda}\, x) & & \qquad \text{if } \; \lambda > 0 , \\ & y(x) = A x + B & & \qquad \text{if } \; \lambda = 0 . \end{aligned}\end{align} \nonumber \]

Veamos si\(\lambda=0\) es un valor propio: Debemos satisfacer\(0=hB-A\) y\(A=0\), por lo tanto\(B=0\) (as\(h>0\)), por lo tanto, no\(0\) es un valor propio (sin solución diferente de cero, por lo que no hay función propia).

Ahora intentemos\(h>0\). Tapamos las condiciones de contorno.

\[\begin{align}\begin{aligned} 0 &=hA- \sqrt{\lambda}B, \\ 0 &=-A\sqrt{\lambda}\sin(\sqrt{\lambda})+B\sqrt{\lambda}\cos(\sqrt{\lambda}).\end{aligned}\end{align} \nonumber \]

Si\(A=0\), entonces\(B=0\) y viceversa, de ahí que ambos sean distintos de cero. Entonces\(B=\frac{hA}{\sqrt{\lambda}}\), y\(0=-A \sqrt{\lambda}\sin(\sqrt{\lambda})+\frac{hA}{\sqrt{\lambda}}\sqrt{\lambda}\cos(\sqrt{\lambda})\). A medida\(A \neq 0\) que obtenemos

\[0=- \sqrt{\lambda}\sin(\sqrt{\lambda})+h\cos(\sqrt{\lambda}), \nonumber \]

o

\[\frac{h}{\sqrt{\lambda}}= \tan \sqrt{\lambda}. \nonumber \]

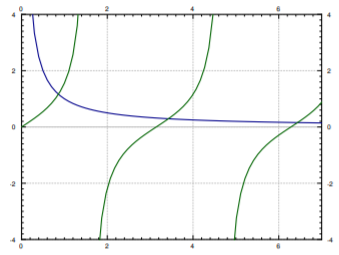
Ahora usa una computadora para encontrar\(\lambda_n\). Hay mesas disponibles, aunque usar una computadora o una calculadora gráfica es mucho más conveniente hoy en día. El método más sencillo es trazar las funciones\(\frac{h}{x}\)\(\tan(x)\) y y ver para qué se cruzan. Hay un número infinito de intersecciones. Denotar la primera intersección por\(\sqrt{\lambda_1}\) la primera intersección, por\(\sqrt{\lambda_2}\) la segunda intersección, etc... Por ejemplo, cuando\(h=1\), lo conseguimos\(\sqrt{\lambda_1}\approx 0.86,\: \sqrt{\lambda_2}\approx 3.43, ...\). Es decir\(\lambda_1 \approx 0.74,\: \lambda_2 \approx 11.73,... \),... Una gráfica para\(h=1\) se da en la Figura\(\PageIndex{1}\). La función propia apropiada (\(A=1\)por conveniencia, entonces\(B= \frac{h}{\sqrt{\lambda}}\)) es

\[y_n(x)=\cos(\sqrt{\lambda_n}x)+\frac{h}{\sqrt{\lambda_n}}\sin(\sqrt{\lambda_n}x). \nonumber \]

Cuando\(h=1\) lleguemos (aproximadamente)

\[y_1(x) \approx \cos(0.86x)+ \frac{1}{0.86} \sin(0.86x),\quad y_2(x) \approx \cos(3.43x)+ \frac{1}{3.43} \sin(3.43x),\quad .... \nonumber \]

Figura\(\PageIndex{1}\): Gráfica de\(\frac{1}{x}\) y\(\tan x\).

Ortogonalidad

Hemos visto antes la noción de ortogonalidad. Por ejemplo, hemos demostrado que\(\sin(nx)\) son ortogonales para distinto\(n\) en\([0, \pi]\). Para problemas generales de Sturm-Liouville necesitaremos una configuración más general. Dejar\(r(x)\) ser una función de peso (cualquier función, aunque generalmente asumiremos que es positiva) on\([a, b]\). Dos funciones\(f(x)\),\(g(x)\) se dice que son ortogonales con respecto a la función de peso\(r(x)\) cuando

\[\int_a^bf(x)g(x)r(x)dx=0. \nonumber \]

En esta configuración, definimos el producto interno como

\[ \langle f,g \rangle \overset{\rm{def}}= \int_a^bf(x)g(x)r(x)dx, \nonumber \]

y luego decir\(f\) y\(g\) son ortogonales cuando sea\(\langle f,g \rangle=0\). Los resultados y conceptos vuelven a ser análogos al álgebra lineal dimensional finita.

La idea del producto interno dado es que aquellos\(x\) donde\(r(x)\) es mayor tengan más peso. Los no triviales (no constantes)\(r(x)\) surgen naturalmente, por ejemplo de un cambio de variables. De ahí, se podría pensar en un cambio de variables tales que\(d \xi =r(x)dx\).

Las funciones propias de un problema regular de Sturm-Liouville satisfacen una propiedad de ortogonalidad, al igual que las funciones propias de la Sección 4.1. Su prueba es muy similar al Teorema análogo 4.1.1.

Teorema\(\PageIndex{2}\)

Supongamos que tenemos un problema regular de Sturm-Liouville

\[\begin{align}\begin{aligned} \frac{d}{dx} \left( p(x) \frac{dy}{dx} \right) -q(x)y+\lambda r(x)y &=0, \\ \alpha_1y(a)- \alpha_2y'(a) &=0, \\ \beta_1y(b)+ \beta_2y'(b) &=0.\end{aligned}\end{align} \nonumber \]

Let\(y_j\) y\(y_k\) ser dos funciones propias distintas para dos valores propios distintos\(\lambda_j\) y\(\lambda_k\). Entonces

\[\int_a^by_j(x)y_k(x)r(x)dx=0, \nonumber \]

es decir,\(y_j\) y\(y_k\) son ortogonales con respecto a la función de peso\(r\).

Fredholm Alternativa

También tenemos el teorema alternativo de Fredholm del que hablamos antes (Teorema 4.1.2) para todos los problemas regulares de Sturm-Liouville. Lo declaramos aquí por completitud.

Teorema\(\PageIndex{3}\)

Fredholm Alternativa

Supongamos que tenemos un problema regular de Sturm-Liouville. Entonces, ya sea

\[\begin{align}\begin{aligned} \frac{d}{dx} \left( p(x) \frac{dy}{dx} \right) -q(x)y+\lambda r(x)y &=0, \\ \alpha_1y(a)- \alpha_2y'(a) &=0, \\ \beta_1y(b)+ \beta_2y'(b) &=0,\end{aligned}\end{align} \nonumber \]

tiene una solución diferente de cero, o

\[\begin{align}\begin{aligned} \frac{d}{dx} \left( p(x) \frac{dy}{dx} \right) -q(x)y+\lambda r(x)y &=f(x), \\ \alpha_1y(a)- \alpha_2y'(a) &=0, \\ \beta_1y(b)+ \beta_2y'(b) &=0,\end{aligned}\end{align} \nonumber \]

tiene una solución única para cualquier\(f(x)\) continuo\([a,b]\).

Este teorema se utiliza de la misma manera que lo hacíamos antes en la Sección 4.4. Se utiliza para resolver problemas de valores de límites no homogéneos más generales. El teorema no nos ayuda a resolver el problema, sino que nos dice cuándo existe una solución única, para que sepamos cuándo dedicar tiempo a buscarla. Para resolver el problema nos descomponemos\(f(x)\) y\(y(x)\) en términos de las funciones propias del problema homogéneo, y luego resolvemos para los coeficientes de la serie para\(y(x)\).

Serie Eigenfunction

Lo que queremos hacer con las funciones propias una vez que las tenemos es calcular la descomposición de la función propia de una función arbitraria\(f(x)\). Es decir, deseamos escribir

\[\label{eq:26} f(x)= \sum_{n=1}^{\infty}c_ny_n(x), \]

donde\(y_n(x)\) las funciones propias. Deseamos saber si podemos representar alguna función de esta\(f(x)\) manera, y si es así, queremos calcular (y por supuesto que querríamos saber si la suma converge). Bien, así que imagina que podríamos escribir\(f(x)\) como\(\eqref{eq:26}\). Asumiremos la convergencia y la capacidad de integrar la serie término por término. Debido a la ortogonalidad tenemos

\[\begin{align}\begin{aligned} \langle f,y_m \rangle &= \int_a^bf(x)y_m(x)r(x)dx \\ &= \sum_{n=1}^{\infty}c_n \int_a^by_n(x)y_m(x)r(x)dx \\ &=c_m \int_a^by_m(x)y_m(x)r(x)dx= c_m \langle y_m,y_m \rangle .\end{aligned}\end{align} \nonumber \]

Por lo tanto,

\[\label{eq:28} c_m= \frac{\langle f,y_m \rangle}{\langle y_m,y_m \rangle}= \frac{\int_a^bf(x)y_m(x)r(x)dx}{\int_a^b(y_m(x))^2r(x)dx}. \]

Tenga en cuenta que\(y_m\) se conocen hasta un múltiplo constante, por lo que podríamos haber escogido un múltiplo escalar de una función propia tal que\(\langle y_m,y_m \rangle=1\) (si tuviéramos una función propia arbitraria\(\tilde{y}_m\), dividirla por\(\sqrt{\langle \tilde{y}_m,\tilde{y}_m \rangle}\)). Cuando\(\langle y_m,y_m \rangle=1\) tenemos la forma más simple\(c_m=\langle f,y_m \rangle\) como lo hicimos para la serie de Fourier. El siguiente teorema se sostiene de manera más general, pero la afirmación dada es suficiente para nuestros propósitos.

Teorema\(\PageIndex{4}\)

Supongamos que\(f\) es una función continua lisa por partes en. Si\(y_1,y_2, \ldots\) son las funciones propias de un problema regular de Sturm-Liouville, entonces existen constantes reales\(c_1,c_2, \ldots\) dadas por\(\eqref{eq:28}\) tal que\(\eqref{eq:26}\) converge y se mantiene para\(a<x<b\).

Ejemplo\(\PageIndex{4}\)

Toma el simple problema de Sturm-Liouville

\[\begin{align}\begin{aligned} & y'' + \lambda y = 0, \quad 0 < x < \frac{\pi}{2} , \\ & y(0) =0, \quad y'(\frac{\pi}{2}) = 0 .\end{aligned}\end{align} \nonumber \]

Lo anterior es un problema regular y además sabemos por Teorema\(\PageIndex{1}\) que\(\lambda \geq 0\).

Supongamos\(\lambda = 0\), entonces la solución general es\(y(x)Ax+B\), enchufamos las condiciones iniciales para obtener\(0=y(0)=B\), y\(0=y'(\pi/2)=A\), por lo tanto, no\(\lambda=0\) es un valor propio. La solución general, por lo tanto, es

\[y(x)=A\cos(\sqrt{\lambda}x)+B\sin(\sqrt{\lambda}x). \nonumber \]

Tapando las condiciones de límite que obtenemos\(0=y(0)=A\) y\(0=y'(\pi/2)=\sqrt{\lambda}B\cos(\sqrt{\lambda}\frac{\pi}{2})\). \(B\)no puede ser cero y por lo tanto\(\cos(\sqrt{\lambda}\frac{\pi}{2}=0)\). Esto significa que\(\sqrt{\lambda}\frac{\pi}{2}\) debe ser un múltiplo integral impar de\(\frac{\pi}{2}\), i.e\((2n-1)\frac{\pi}{2}=\sqrt{\lambda_n}\frac{\pi}{2}\). De ahí

\[\lambda_n=(2n-1)^2. \nonumber \]

Podemos tomar\(B=1\). De ahí que nuestras funciones propias sean

\[ y_n(x)= \sin((2n-1)x). \nonumber \]

Finalmente calculamos

\[ \int_0^{\frac{\pi}{2}}(\sin((2n-1)x))^2dx=\frac{\pi}{4}. \nonumber \]

Así que cualquier función lisa por partes encendida se\([0, \pi/2]\) puede escribir como

\[f(x)=\sum_{n=1}^{\infty}c_n\sin((2n-1)x), \nonumber \]

donde

\[c_n= \frac{\langle f,y_n \rangle}{\langle y_n,y_n \rangle}= \frac{\int_0^{\frac{\pi}{2}}\sin((2n-1)x)dx}{\int_0^{\frac{\pi}{2}}(\sin((2n-1)x))^2dx}= \frac{4}{\pi} \int f(x)_{0}^{\frac{\pi}{2}}\sin((2n-1)x)dx. \nonumber \]

Tenga en cuenta que la serie converge a un impar\(2\pi\) -periódico (¡no\(\pi\) -periódico!) extensión de\(f(x)\).

Ejercicio\(\PageIndex{3}\)

En el ejemplo anterior, la función se define en\(0<x< \pi/2\), sin embargo, la serie con respecto a las funciones propias\(\sin ((2n-1)x)\) converge a una extensión impar\(2\pi\) -periódica de\(f(x)\). Descubre cómo se define la extensión para\(\pi/2 <x< \pi\).

Calculemos un ejemplo. Considerar\(f(x) = x\) para\(0 < x < \frac{\pi}{2}\). Algún cálculo más adelante nos encontramos\[c_n = \frac{4}{\pi} \int_0^{\frac{\pi}{2}} f(x) \,\sin \bigl( (2n-1)x \bigr) \, dx = \frac{4{(-1)}^{n+1}}{\pi {(2n-1)}^2} , \nonumber \] y así para\(x\) en\([0,\frac{\pi}{2}]\),\[f(x) = \sum_{n=1}^\infty \frac{4{(-1)}^{n+1}}{\pi {(2n-1)}^2} \sin \bigl( (2n-1)x \bigr) . \nonumber \]

Esto es diferente de la serie sinusoidal regular\(\pi\) -periódica que se puede calcular para ser

\[f(x)=\sum\limits_{n=1}^\infty \frac{(-1)^{n+1}}{n}\sin (2nx). \nonumber \]

Ambas sumas convergen son iguales a\(f(x)\) for\(0 < x < \frac{\pi}{2}\), pero las funciones propias involucradas provienen de diferentes problemas de autovalor.

Notas al pie

[1] El nombre de los matemáticos franceses Jacques Charles François Sturm (1803—1855) y Joseph Liouville (1809—1882).