6.5: Resolviendo PDEs con la Transformación de Laplace
- Page ID
- 115263
La transformada de Laplace proviene de la misma familia de transformaciones que la serie de Fourier \(^{1}\), que utilizamos en el Capítulo 4 para resolver ecuaciones diferenciales parciales (PDE). Por lo tanto, no es sorprendente que también podamos resolver las PDE con la transformación de Laplace.
Dada una PDE en dos variables independientes\(x\) y\(t\), utilizamos la transformada de Laplace en una de las variables (tomando la transformación de todo a la vista), y las derivadas en esa variable se convierten en multiplicaciones por la variable transformada\(s\). El PDE se convierte en una ODE, que resolvemos. Posteriormente invertimos la transformación para encontrar una solución al problema original. Lo mejor es ver el procedimiento en un ejemplo.
Considera la PDE de primer orden\[y_t = - \alpha y_x, \qquad \text{for } x > 0, \enspace t > 0, \nonumber \] con condiciones laterales\[y(0,t) = C, \qquad y(x,0) = 0 . \nonumber \] Esta ecuación se llama la ecuación de convección o a veces la ecuación de transporte, y ya hizo aparición en la Sección 1.9, con diferentes condiciones. Consulte la Figura\(\PageIndex{1}\) para ver un diagrama de la configuración.
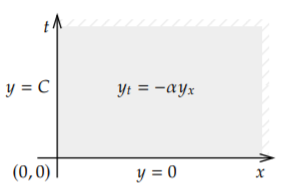
Una configuración física de esta ecuación es un río de sustancia goo sólida, ya que no queremos que nada se difume. La función\(y\) es la concentración de alguna sustancia tóxica. \(^{2}\)La variable\(x\) denota posición donde\(x=0\) se encuentra la ubicación de una fábrica que arroja la sustancia tóxica al río. La sustancia tóxica desemboca en el río para que a\(x=0\) la concentración esté siempre\(C\). Deseamos ver qué pasa más allá de la fábrica, es decir, en\(x > 0\). \(t\)Sea el momento, y supongamos que la fábrica inició operaciones en\(t=0\), de modo que en\(t=0\) el río es solo pura sustancia goo.
Considerar una función de dos variables\(y(x,t)\). Arreglemos\(x\) y transformemos la\(t\) variable. Por conveniencia, tratamos la\(s\) variable transformada como un parámetro, ya que no hay derivadas en\(s\). Es decir, escribimos\(Y(x)\) para la función transformada, y la tratamos como una función de\(x\), dejando\(s\) como parámetro. \[Y(x) = {\mathcal L} \bigl\{ y(x,t) \bigr\} = \int_0^\infty y(x,t) e^{-st} \,ds . \nonumber \]
La transformación de una derivada con respecto a\(x\) es simplemente diferenciar la función transformada:\[{\mathcal L} \bigl\{ y_x(x,t) \bigr\} = \int_0^\infty y_x(x,t) e^{-st} \,ds = \frac{d}{dx} \left[\int_0^\infty y(x,t) e^{-st} \,ds \right] = Y'(x) . \nonumber \]
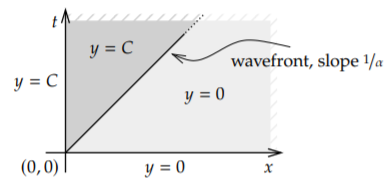
Para transformar la derivada en\(t\) (la variable que se está transformando), utilizamos las reglas de la Sección 6.2:\[{\mathcal L} \bigl\{ y_t(x,t) \bigr\} = sY(x) - y(x,0) . \nonumber \] En nuestro caso específico,\(y(x,0)=0\), y así\({\mathcal L} \bigl\{ y_t(x,t) \bigr\} = sY(x)\). Transformamos la ecuación para encontrar\[sY(x) = -\alpha Y'(x) . \nonumber \] Esta ODE necesita una condición inicial. La condición inicial es la otra condición lateral de la PDE, la que depende\(x\). Todo se transforma, así que también debemos transformar esta condición\[Y(0) = {\mathcal L} \bigl\{ y(0,t) \bigr\} = {\mathcal L} \bigl\{ C \bigr\} = \frac{C}{s} . \nonumber \] Resolvemos el problema de la ODE\(sY(x) = -\alpha Y'(x)\)\(Y(0) = \frac{C}{s}\),, para encontrar No\[Y(x) = \frac{C}{s} e^{-\frac{s}{\alpha} x} . \nonumber \] hemos terminado, tenemos \(Y(x)\), pero realmente queremos\(y(x,t)\). Transformamos la\(s\) variable de nuevo a\(t\). \[u(t) = \begin{cases} 0 & \text{if $t < 0$}, \\ 1 & \text{otherwise} \end{cases} \nonumber \]Sea la función Heaviside. Como\[{\mathcal L} \bigl\{ u(t-a) \bigr\} = \int_0^\infty u(t-a) \, e^{-st} \,dt = \int_a^\infty e^{-st} \,dt = \frac{e^{-as}}{s} , \nonumber \] entonces\[y(x,t) = {\mathcal L}^{-1} \left\{ \frac{C}{s} e^{-\frac{s}{\alpha} x} \right\} = C u\bigl(t-\frac{x}{\alpha}\bigr) . \nonumber \] En otras palabras,\[y(x,t) = \begin{cases} 0 & \text{if $t < \frac{x}{\alpha}$}, \\ C & \text{otherwise.} \end{cases} \nonumber \]
Ver Figura\(\PageIndex{2}\) for a diagram of this solution. The line of slope \(\frac{1}{\alpha}\) indica el frente de onda de la sustancia tóxica en la imagen a medida que sale de fábrica. Lo que hace la ecuación es simplemente mover la condición inicial hacia la derecha a velocidad\(\alpha\).
Shhh... no\(y\) es diferenciable, ni siquiera es continuo (nadie parece darse cuenta nunca). ¿Cómo podríamos enchufar algo que no es diferenciable en la ecuación? Bueno, solo piensa en una función diferenciable muy, muy cercana a\(y\). O bien, si reconoces la derivada de la función Heaviside como la función delta, entonces todo está bien también:\[y_t (x,t) = \frac{\partial}{\partial t} \left[ C u\bigl(t-\frac{x}{\alpha}\bigr) \right] = C u'\bigl(t-\frac{x}{\alpha}\bigr) = C \delta\bigl(t-\frac{x}{\alpha}\bigr) \nonumber \] y\[y_x (x,t) = \frac{\partial}{\partial x} \left[ C u\bigl(t-\frac{x}{\alpha}\bigr) \right] = - \frac{C}{\alpha} u'\bigl(t-\frac{x}{\alpha}\bigr) = - \frac{C}{\alpha} \delta\bigl(t-\frac{x}{\alpha}\bigr) . \nonumber \] So\(y_t = - \alpha y_x\).
La ecuación de Laplace es muy buena con ecuaciones de coeficiente constante. Una ventaja de Laplace es que maneja fácilmente condiciones laterales no homogéneas. Probemos un ejemplo más complicado.
Consideremos\[\begin{align}\begin{aligned} & y_t + y_x + y = 0, \qquad \text{for } x > 0, \enspace t > 0, \\ & y(0,t) = \sin(t), \qquad y(x,0) = 0 .\end{aligned}\end{align} \nonumber \] De nuevo, transformamos\(t\), y escribimos\(Y(x)\) para la función transformada. Como\(y(x,0) = 0\), encontramos\[sY(x) + Y'(x) + Y(x) = 0, \qquad Y(0) = \frac{1}{s^2+1} . \nonumber \] La solución de la ecuación transformada es\[Y(x) = \frac{1}{s^2+1} e^{-(s+1) x} = \frac{1}{s^2+1} e^{-xs} e^{-x} . \nonumber \] Usando la segunda propiedad de desplazamiento (6.2.14) y linealidad de la transformada, obtenemos la solución\[y(x,t) = e^{-x} \sin(t-x) u(t-x) . \nonumber \]
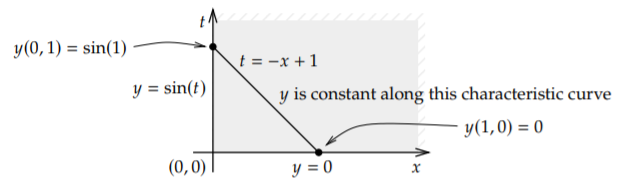
También podemos detectar cuando el problema está en el sentido de que no tiene solución. Cambiemos la ecuación a\[\begin{align}\begin{aligned} & -y_t + y_x = 0, \qquad \text{for } x > 0, \enspace t > 0, \\ & y(0,t) = \sin(t), \qquad y(x,0) = 0 .\end{aligned}\end{align} \nonumber \]
Entonces el problema no tiene solución. Primero, veamos esto en el lenguaje de la Sección 1.9. Las curvas características son\(t=-x+C\). Si\(\tau\) es la coordenada característica, entonces encontramos la ecuación\(y_\tau = 0\) a lo largo de la curva, lo que significa que una solución es constante a lo largo de curvas características. Pero estas curvas se cruzan tanto con el\(x\) eje -eje como\(t\) con el eje. Por ejemplo, la curva\(t=-x+1\) se cruza en\((1,0)\) y\((0,1)\). La solución es constante a lo largo de la curva por lo que\(y(1,0)\) debe ser igual\(y(0,1)\). Pero\(y(1,0) = 0\) y\(y(0,1) = \sin(1) \not= 0\). Ver Figura\(\PageIndex{3}\).
Ahora considera la transformación. El problema transformado es\[-sY(x) + Y'(x) = 0, \enspace Y(0) = \frac{1}{s^2+1} , \nonumber \] y la solución debería ser ¡\[Y(x) = \frac{1}{s^2+1} e^{sx} . \nonumber \]Es importante destacar que esta transformada de Laplace no decae a cero al infinito! Es decir, ya que\(x > 0\) en la región de interés, entonces casi\[\lim_{s \to \infty} \frac{1}{s^2+1} e^{sx} = \infty \not= 0 . \nonumber \] parece como si pudiéramos usar la propiedad desplazable, pero fíjense que el cambio va en la dirección equivocada. Por supuesto, no necesitamos restringirnos a ecuaciones de primer orden, aunque los cálculos se involucran más para las ecuaciones de orden superior.
Usemos Laplace para el siguiente problema:
\[\begin{aligned} & y_t = y_{xx}, \qquad 0 < x < \infty, \enspace t > 0,\\ & y_x(0,t) = f(t), \\ & y(x,0) = 0 .\end{aligned} \nonumber \]Realmente también imponemos otras condiciones a la solución para que por ejemplo exista la transformación de Laplace. Por ejemplo, podríamos imponer que\(y\) esté acotado por cada tiempo fijo\(t\). Transformar la ecuación en la\(t\) variable para encontrar\[sY(x) = Y''(x) . \nonumber \] La solución general a esta ODE es\[Y(x) = A e^{\sqrt{s}x} + B e^{-\sqrt{s} x} . \nonumber \] Primero\(A=0\), ya que de lo contrario\(Y\) no decae a cero como\(s \to \infty\). Ahora considere la condición de límite. Transformar\(Y'(0) = F(s)\) y así\(-\sqrt{s}B = F(s)\). En otras palabras,\[Y(x) = - F(s) \frac{1}{\sqrt{s}} e^{-\sqrt{s} x} . \nonumber \]
Si buscamos la transformación inversa en una tabla como la del Apéndice B (o pasamos la tarde haciendo cálculo), encontramos\[{\mathcal L}^{-1}\left[e^{-\sqrt{s} x}\right] = \frac{x}{\sqrt{4\pi t^3}} e^{\frac{-x^2}{4t}} , \nonumber \] o\[{\mathcal L}^{-1}\left[\frac{1}{\sqrt{s}} e^{-\sqrt{s} x}\right] = \frac{1}{\sqrt{\pi t}} e^{\frac{-x^2}{4t}} . \nonumber \] So\[y(x,t) = {\mathcal L}^{-1} \left[ F(s) e^{-\sqrt{s} x}\right] = \int_0^t f(\tau) \frac{1}{\sqrt{\pi {(t-\tau)}}} e^{\frac{-x^2}{4(t-\tau)}} \, d\tau . \nonumber \]
Laplace puede resolver problemas donde falla la separación de variables. A Laplace no le importa la no homogeneidad, pero esencialmente solo es útil para ecuaciones de coeficientes constantes.

