6.4: Delta Dirac y Respuesta al Impulso

Pulso Rectangular

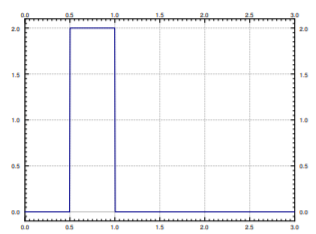
A menudo en aplicaciones estudiamos un sistema físico poniendo un pulso corto y luego viendo lo que hace el sistema. El comportamiento resultante a menudo se llama respuesta de impulso. Veamos a qué nos referimos con pulso. El tipo más simple de pulso es un pulso rectangular simple definido por

\[ \varphi(t)= \left\{ \begin{array}{ccc} 0 & {\rm{if~}}~~~~t<a, \\ M & {\rm{if~}}a \leq t<b, \\ 0 & {\rm{if~}}b \leq t.\end{array} \right. \nonumber \]

Observe que\[\varphi (t) = M\left(u(t-a)-u(t-b)\right), \nonumber \] dónde\(u(t)\) está la función de paso de unidad (ver Figura\(\PageIndex{1}\) para una gráfica).

Figura\(\PageIndex{1}\): Pulso cuadrado de muestra con\(a=0.5\)\(b=1\), y\(M=2\).

Tomemos la transformación de Laplace de un pulso cuadrado,

\[\begin{align}\begin{aligned} \mathcal{L}\{ \varphi(t)\} &= \mathcal{L}\{ M(u(t-a)-u(t-b)) \} &= M \frac{e^{-as}-e^{-bs}}{s}.\end{aligned}\end{align} \nonumber \]

Por simplicidad dejamos\(a=0\) y es conveniente configurar\(M= \dfrac{1}{b}\) para tener

\[ \int _0 ^{\infty} \varphi (t) \; dt = 1 \nonumber \]

Es decir, para que el pulso tenga “masa unitaria”. Para tal pulso calculamos

\[ \mathcal{L}\{ \varphi(t)\}= \mathcal{L}\left\{ \frac{u(t)-u(t-b)}{b} \right\} = \frac{1-e^{-bs}}{bs}. \nonumber \]

Generalmente queremos\(b\) ser muy pequeños. Es decir, deseamos que el pulso sea muy corto y muy alto. Al dejar\(b\) ir a cero llegamos al concepto de la función delta de Dirac.

6.4.2Función Delta

La función delta de Dirac no \(^{1}\)es exactamente una función; a veces se le llama función generalizada. Evitamos detalles innecesarios y simplemente decimos que es un objeto que realmente no tiene sentido a menos que lo integremos. La motivación es que nos gustaría una “función”\(\delta (t)\) tal que para cualquier función continua que\(f(t)\) tengamos

\[ \int_{-\infty}^{\infty} \delta (t) f(t) \, dt = f(0) \nonumber \]

La fórmula debe sostenerse si integramos sobre cualquier intervalo que contenga 0, no solo\((-\infty, \infty)\). Así\(\delta (t)\) es una “función” con toda su “masa” en un solo punto\(t=0\). En otras palabras, para cualquier intervalo\([c,d]\)

\[ \int_c^d \delta(t)= \left\{ \begin{array}{cl} 1 & {\rm{if~the~interval~}} [c,d]{\rm{~contains~}}0, {\rm{~i.e.~}}c \leq 0 \leq d, \\ 0 & {\rm{otherwise}}. \end{array} \right. \nonumber \]

Desafortunadamente no existe tal función en el sentido clásico. Se podría pensar informalmente que\(\delta (t)\) es cero para\(t \neq 0\) y de alguna manera infinito en\(t=0\).

Una buena manera de pensar\(\delta (t)\) es como un límite de pulsos cortos cuya integral es 1. Por ejemplo, supongamos que tenemos un pulso cuadrado\(\varphi (t)\) como arriba con\(a=0\),\(M=\dfrac{1}{b}\), es decir\(\varphi (t) = \dfrac{u(t)-u(t-b)}{b} \).

Compute

\[ \int_{-\infty}^{\infty} \varphi (t) f(t) \, dt = \int_{-\infty}^{\infty} \dfrac{u(t)-u(t-b)}{b} f(t) \, dt =\dfrac{1}{b} \int_{0}^{b} f(t) \, dt. \nonumber \]

Si\(f(t)\) es continuo en\(t=0\), entonces para muy pequeños\(b\), la función\(f(t)\) es aproximadamente igual a\(f(0)\) en el intervalo\([0,b)\). Aproximamos la integral

\[ \dfrac{1}{b} \int_0^b f(t) \, dt \approx \dfrac{1}{b} \int_0^b f(t) \, dt = f(0). \nonumber \]

Por lo tanto,

\[ \lim _{b \rightarrow 0} \int_{-\infty}^{\infty} \varphi (t) f(t) \, dt = \lim _{b \rightarrow 0} \dfrac{1}{b} \int_0^b f(t) \, dt = f(0) \nonumber \]

Por lo tanto, aceptemos\(\delta (t)\) como un objeto que es posible integrar. Muchas veces queremos pasar\(\delta\) a otro punto, por ejemplo\(\delta (t-a)\). En ese caso tenemos

\[ \int_{-\infty}^{\infty} \delta(t-a) f(t) \, dt = f(a). \nonumber \]

Tenga en cuenta que\(\delta (a-t)\) es el mismo objeto que\(\delta (t-a)\). En otras palabras, la convolución de\(\delta (t)\) con\(f(t)\) es de nuevo\(f(t)\),

\[ (f * \delta)(t) = \int _0^t \delta(t-s)f(s)\, ds = f(t) \nonumber \]

A medida que podamos integrarnos\(\delta (t)\), calculemos su transformación de Laplace.

\[ \mathcal{L} \{\delta (t-a) \} = \int_0^{\infty} e^{-st} \delta(t-a) \, dt = e^{-as}. \nonumber \]

En particular,

\[ \mathcal{L} \{\delta (t) \} = 1. \nonumber \]

Nota

Observe que la transformación de Laplace\(\delta (t-a)\) se parece a la transformada de Laplace de la derivada de la función Heaviside\(u(t-a)\), si pudiéramos diferenciar la función Heaviside. Primer aviso

\[ \mathcal{L} \{\delta (t-a) \} = \dfrac{e^{-as}}{s}. \nonumber \]

Para obtener lo que sería la transformación de Laplace de la derivada nos multiplicamos por\(s\), para obtener\(e^{-as}\), que es la transformación de Laplace de\(\delta (t-a)\). Vemos lo mismo usando la integración,

\[ \int _0^{t} \delta (s-a) \,ds = u(t-a) \nonumber \]

Entonces, en cierto sentido

\[ \dfrac{d}{dt} [u(t-a)] = \delta(t-a) \nonumber \]

Esta línea de razonamiento nos permite hablar de derivadas de funciones con discontinuidades de salto. Podemos pensar que la derivada de la función\(u(t-a)\) Heaviside es de alguna manera infinita en\(a\), que es precisamente nuestra comprensión intuitiva de la función delta.

Ejemplo\(\PageIndex{1}\)

Compute

\[ \mathcal{L}^{-1} \left\{ \dfrac{s+1}{s} \right\}. \nonumber \]

Hasta ahora siempre hemos mirado las funciones racionales adecuadas en la\(s\) variable. Es decir, el numerador siempre fue de menor grado que el denominador. No es así con\(\dfrac{s+1}{s}\). Escribimos,

\[ \mathcal{L}^{-1} \left\{ \dfrac{s+1}{s} \right\} = \mathcal{L}^{-1} \left\{ 1+ \dfrac{1}{s} \right\} = \mathcal{L}^{-1} \{1\} + \mathcal{L}^{-1} \left\{ \dfrac{1}{s} \right\} = \delta(t) + 1. \nonumber \]

El objeto resultante es una función generalizada y solo tiene sentido cuando se pone debajo de una integral.

Respuesta al Impulso

Como dijimos antes, en la ecuación diferencial\( Lx = f(t)\), pensamos en\(f(t)\) ello como input, y\(x(t)\) como output. A menudo es importante encontrar la respuesta a un impulso, y luego usamos la función delta en lugar de\(f(t)\). La solución para

\[ Lx = \delta (t) \nonumber \]

se llama la respuesta al impulso.

Ejemplo\(\PageIndex{2}\)

Resolver (encontrar la respuesta al impulso)

\[\label{eq:20} x'' + \omega_0^2x=\delta(t) ,\quad x(0)=0 ,\quad x'(0)=0. \]

Primero aplicamos la transformada de Laplace a la ecuación. Denotar la transformación de\(x(t)\) por\(X(s)\).

\[ s^2X(s) + \omega^2_0X(s) = 1,\quad\text{and so}\quad X(s) = \dfrac{1}{s^2+\omega^2_0}. \nonumber \]

Tomando la transformada inversa de Laplace obtenemos

\[x(t)=\frac{\sin (\omega_{0}t)}{\omega_{0}}. \nonumber \]

Notemos algo sobre el ejemplo anterior. En el Ejemplo 6.3.4, encontramos que cuando la entrada era\(f(t)\), entonces la solución a\( Lx = f(t)\) fue dada por

\[ x(t) = \int_0^t f(\tau)\dfrac{\sin \left(\omega_0(t-\tau) \right)}{\omega_0} d\tau. \nonumber \]

Observe que la solución para una entrada arbitraria se da como convolución con la respuesta de impulso. Veamos por qué. La clave es notar que para funciones\(x(t)\) y\(f(t)\),

\[ (x*f)''(t) = \dfrac{d^2}{dt^2} \left[ \int_0^t f(\tau)x(t-\tau)\,d\tau \right] = \int _0^t f(\tau)x''(t-\tau)\, d\tau = (x'' * f)(t). \nonumber \]

Simplemente diferenciamos dos veces bajo la integral, \(^{2}\)los detalles se dejan como ejercicio. Y así, si convolvemos toda la ecuación\(\eqref{eq:20}\), el lado izquierdo se vuelve

\[ (x'' + \omega_0^2x)* f = (x'' * f) + \omega_0^2(x*f) = (x*f)'' + \omega_0^2(x*f). \nonumber \]

El lado derecho se convierte en

\[ (\delta * f)(t) = f(t). \nonumber \]

Por lo tanto,\(y(t) = (x*f)(t)\) es la solución para

\[ y'' + \omega_0^2y = f(t). \nonumber \]

Este procedimiento funciona en general para otras ecuaciones lineales\(Lx=f(t)\). Si determina la respuesta de impulso, también sabe cómo obtener la salida\(x(t)\) para cualquier entrada\(f(t)\) simplemente convolucionando la respuesta de impulso y la entrada\(f(t)\).

Doblado de viga de tres puntos

Demos otro ejemplo bastante diferente donde aparece la función delta: Representando cargas puntuales en una viga de acero. Considera una viga de longitud\(L\), apoyada sobre dos simples soportes en los extremos. Dejar\(x\) denotar la posición en la viga, y dejar\(y(x)\) denotar la deflexión de la viga en la dirección vertical. La deflexión\(y(x)\) satisface la ecuación de Euler-Bernoulli, \(^{3}\)\[EI \frac{d^4 y}{dx^4} = F(x) , \nonumber \]donde\(E\) y\(I\) son constantes \(^{4}\)y\(F(x)\) es la fuerza aplicada por unidad de longitud en la posición\(x\). La situación que nos interesa es cuando la fuerza se aplica en un solo punto como en la Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): Flexión de tres puntos.

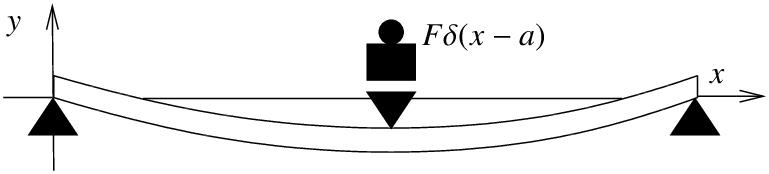
En este caso la ecuación se convierte

\[ EI\dfrac{d^4y}{dx^4}=-F\delta(x-a) \nonumber \]

donde\(x=a\) es el punto donde se aplica la masa. \(F\)es la fuerza aplicada y el signo menos indica que la fuerza es descendente, es decir, en la\(y\) dirección negativa. Los puntos finales de la viga satisfacen las condiciones,

\[\begin{align}\begin{aligned} & y(0) = 0, \qquad y''(0) = 0, \\ & y(L) = 0, \qquad y''(L) = 0.\end{aligned}\end{align} \nonumber \]

Consulte la Sección 5.2, para obtener más información sobre las condiciones de punto final aplicadas a las vigas.

Ejemplo\(\PageIndex{3}\)

Supongamos que la longitud de la viga es\(2\), y supongamos que\(EI=1\) por simplicidad. Supongamos además que la fuerza\(F=1\) se aplica en\(x=1\). Es decir, tenemos la ecuación

\[ \dfrac{d^4y}{dx^4}=-\delta(x-1) \nonumber \]

y las condiciones de punto final son

\[ y(0)=0,\quad y''(0)=0,\quad y(2)=0,\quad y''(2)=0. \nonumber \]

Podríamos integrarnos, pero usar la transformación de Laplace es aún más fácil. Aplicamos la transformación en la\(x\) variable más que en la\(t\) variable. Denotemos nuevamente la transformación de\(y(x)\) as\(Y(s)\).

\[ s^4Y(s)-s^3y(0)-s^2y'(0)-sy''(0)-y'''(0)=-e^{-s}. \nonumber \]

Nos damos cuenta de que\(y(0)=0\) y\(y''(0)=0\). Llamemos\(C_1=y'(0)\) y\(C^2=y'''(0)\). Resolvemos para\(Y(s)\),

\[ Y(s)=\frac{-e^{-s}}{s^4}+\frac{C_1}{s^2}+\frac{C_2}{s^4}. \nonumber \]

Tomamos la transformada inversa de Laplace utilizando la segunda ecuación de propiedad de desplazamiento (6.2.14) para tomar la inversa del primer término.

\[ y(x)=\frac{-(x-1)^3}{6}u(x-1)+C_1x+ \frac{C_2}{6}x^3. \nonumber \]

Todavía necesitamos aplicar dos de las condiciones de punto final. Como están las condiciones\(x=2\) podemos simplemente sustituir a la\(u(x-1)=1\) hora de tomar los derivados. Por lo tanto,

\[ 0=y(2)=\frac{-(2-1)^3}{6}+C_1(2)+ \frac{C_2}{6}2^3=\frac{-1}{6}+2C_1+\frac{4}{3C_2}, \nonumber \]

y

\[0 = y''(2) = \frac{-3\cdot 2 \cdot (2-1)}{6} + \frac{C_2}{6} 3\cdot 2 \cdot 2 = -1 + 2 C_2 \nonumber \]

De ahí\(C_2 = \frac{1}{2}\) and solving for \(C_{1}\) using the first equation we obtain \(C_1 = \frac{-1}{4}\). Our solution for the beam deflection is \[y(x) = \frac{-{(x-1)}^3}{6} u(x-1) - \frac{x}{4} + \frac{x^3}{12}. \nonumber \]

Notas al pie

[1] Nombrado así por el físico y matemático inglés Paul Adrien Maurice Dirac (1902—1984).

[2] Realmente deberías pensar en la integral repasando\((-\infty , \infty )\) más que sobre\([0,t]\) y simplemente asumir eso\(f(t)\) y\(x(t)\) son continuos y cero para negativos.

[3] Llamado así por los matemáticos suizos Jacob Bernoulli (1654—1705), Daniel Bernoulli —sobrino de Jacob— (1700—1782), y Leonhard Paul Euler (1707—1783).

[4]\(E\) es el módulo elástico y\(I\) es el segundo momento de área. No nos preocupemos por los detalles y simplemente pensemos en estos como algunas constantes dadas.