2.1: Ecuaciones Lineales de Primer Orden
- Page ID
- 115172
Se dice que una ecuación diferencial de primer orden es lineal si se puede escribir como
\[\label{eq:2.1.1} y' + p(x)y = f(x).\]
Una ecuación diferencial de primer orden que no se puede escribir así es no lineal. Decimos que la Ecuación\ ref {eq:2.1.1} es homogénea si\(f \equiv 0\); de lo contrario es no homogénea. Dado que\(y \equiv 0\) es obviamente una solución de la ecuación homogénea
\[y' + p(x)y = 0, \nonumber\]
lo llamamos la solución trivial. Cualquier otra solución no es trivial.
Las ecuaciones de primer orden
\[\begin{aligned} x ^ { 2 } y ^ { \prime } + 3 y & = x ^ { 2 } \\[4pt] x y ^ { \prime } - 8 x ^ { 2 } y & = \sin x \\[4pt] x y ^ { \prime } + ( \ln x ) y & = 0 \\[4pt] y ^ { \prime } & = x ^ { 2 } y - 2 \end{aligned}\]
no están en la forma en la Ecuación\ ref {eq:2.1.1}, sino que son lineales, ya que pueden reescribirse como
\[\begin{aligned} y ^ { \prime } + \frac { 3 } { x ^ { 2 } } y & = 1 \\[4pt] y ^ { \prime } - 8 x y & = \frac { \sin x } { x } \\[4pt] y ^ { \prime } + \frac { \ln x } { x } y & = 0 \\[4pt] y ^ { \prime } - x ^ { 2 } y & = - 2 \end{aligned}\]
Aquí hay algunas ecuaciones no lineales de primer orden:
\[\begin{aligned} x y ^ { \prime } + 3 y ^ { 2 } & = 2 x & \text { (because } y \text { is squared) } \\[4pt] y y ^ { \prime } & = 3 & \text { (because of the product } y y ^ { \prime } ) \\[4pt] y ^ { \prime } + x e ^ { y } & = 12 & \text { (because of } e ^ { y } ) \end{aligned}\]
Solución General de una Ecuación Lineal de Primer Orden
Para motivar una definición que necesitaremos, considere la ecuación lineal simple de primer orden
\[\label{eq:2.1.2} y'={1\over x^2}.\]
A partir del cálculo sabemos que\(y\) satisface esta ecuación si y solo si
\[\label{eq:2.1.3} y=-{1\over x}+c,\]
donde\(c\) es una constante arbitraria. Llamamos a\(c\) un parámetro y decimos que la ecuación\ ref {eq:2.1.3} define una familia de funciones de un parámetro. Para cada número real\(c\), la función definida por la Ecuación\ ref {eq:2.1.3} es una solución de la Ecuación\ ref {eq:2.1.2} on\((-\infty,0)\) y\((0,\infty)\); además, cada solución de Ecuación\ ref {eq:2.1.2} en cualquiera de estos intervalos es de la forma Ecuación\ ref {eq:2.1.3} para alguna elección de\(c\). Decimos que la Ecuación\ ref {eq:2.1.3} es la solución general de la Ecuación\ ref {eq:2.1.2}.
Veremos que ocurre una situación similar en relación con cualquier ecuación lineal de primer orden
\[\label{eq:2.1.4} y'+p(x)y=f(x);\]
es decir, si\(p\) y\(f\) son continuos en algún intervalo abierto\((a,b)\) entonces hay una fórmula única\(y=y(x,c)\) análoga a la ecuación\ ref {eq:2.1.3} que implica\(x\) y un parámetro\(c\) y tiene las siguientes propiedades:
- Para cada valor fijo de\(c\), la función resultante de\(x\) es una solución de Ecuación\ ref {eq:2.1.4} on\((a,b)\).
- Si\(y\) es una solución de la Ecuación\ ref {eq:2.1.4} on\((a,b)\), entonces se\(y\) puede obtener de la fórmula eligiendo\(c\) apropiadamente.
Llamaremos a\(y=y(x,c)\) la solución general de Ecuación\ ref {eq:2.1.4}.
Cuando esto se haya establecido, se seguirá que una ecuación de la forma
\[\label{eq:2.1.5} P_0(x)y'+P_1(x)y=F(x)\]
tiene una solución general en cualquier intervalo abierto\((a,b)\) en el que\(P_0\),\(P_1\), y\(F\) son todos continuos y no\(P_0\) tiene ceros, ya que en este caso podemos reescribir la Ecuación\ ref {eq:2.1.5} en la forma Ecuación\ ref {eq:2.1.4} con\(p=P_1/P_0\) y\(f=F/P_0\), que son ambas continuas en \((a,b)\).
Para evitar una redacción incómoda en ejemplos y ejercicios, no especificaremos el intervalo\((a,b)\) cuando solicitemos la solución general de una ecuación lineal específica de primer orden. Vamos a estar de acuerdo en que esto siempre significa que queremos la solución general en cada intervalo abierto sobre el cual\(p\) y\(f\) son continuos si la ecuación es de la forma Ecuación\ ref {eq:2.1.4}, o sobre cuál\(P_0\)\(P_1\),, y\(F\) son continuas y no\(P_0\) tiene ceros, si la ecuación es de la forma Ecuación\ ref {eq:2.1.5}. Te dejamos identificar estos intervalos en ejemplos y ejercicios específicos.
Para completar, señalamos que si\(P_0\),\(P_1\), y\(F\) son todos continuos en un intervalo abierto\((a,b)\), pero\(P_0\) sí tienen un cero adentro\((a,b)\), entonces la Ecuación\ ref {eq:2.1.5} puede fallar en tener una solución general\((a,b)\) en el sentido justo definido. Dado que este no es un punto importante que deba desarrollarse en profundidad, no lo discutiremos más; sin embargo, vea el Ejercicio 2.1.44 para un ejemplo.
Ecuaciones homogéneas lineales de primer orden
Comenzamos con el problema de encontrar la solución general de una ecuación lineal homogénea de primer orden. El siguiente ejemplo recuerda un resultado familiar del cálculo.
Que\(a\) sea una constante.
- Encuentre la solución general de\[y'-ay=0.\label{eq:2.1.6}\]
- Resolver el problema de valor inicial\[y'-ay=0,\quad y(x_0)=y_0.\nonumber \]
Solución a
(a) Ya sabes por cálculo que si\(c\) es alguna constante, entonces\(y=ce^{ax}\) satisface la Ecuación\ ref {eq:2.1.6}. Sin embargo, pretendamos que lo has olvidado y utilicemos este problema para ilustrar un método general para resolver una ecuación lineal homogénea de primer orden.
Sabemos que la Ecuación\ ref {eq:2.1.6} tiene la solución trivial\(y\equiv0\). Ahora supongamos que\(y\) es una solución no trivial de la Ecuación\ ref {eq:2.1.6}. Entonces, dado que una función diferenciable debe ser continua, debe haber algún intervalo abierto\(I\) en el que no\(y\) tenga ceros. Reescribimos la ecuación\ ref {eq:2.1.6} como
\[{y'\over y}=a \nonumber\]
para\(x\) en\(I\). Integrar esto demuestra que
\[\ln|y|=ax+k,\quad \text{so} \quad |y|=e^ke^{ax}, \nonumber\]
donde\(k\) es una constante arbitraria. Ya que nunca\(e^{ax}\) puede ser igual a cero, no\(y\) tiene ceros, por lo que o siempre\(y\) es positivo o siempre negativo. Por lo tanto podemos reescribir\(y\) como
\[\label{eq:2.1.7} y=ce^{ax}\]
donde
\[c=\left\{\begin{array}{cl}\phantom{-}e^k&\text{if} y>0, \\[4pt] -e^k&\text{if} y<0.\end{array}\right. \nonumber\]
Esto demuestra que cada solución no trivial de la Ecuación\ ref {eq:2.1.6} es de la forma\(y=ce^{ax}\) para alguna constante distinta de cero\(c\). Dado que el ajuste\(c=0\) produce la solución trivial, todas las soluciones de la Ecuación\ ref {eq:2.1.6} tienen la forma Ecuación\ ref {eq:2.1.7}. Por el contrario, la Ecuación\ ref {eq:2.1.7} es una solución de la Ecuación\ ref {eq:2.1.6} para cada elección de\(c\), ya que diferenciar la Ecuación\ ref {eq:2.1.7} rinde\(y'=ace^{ax}=ay\).
Solución b
Imponiendo los\(y(x_0)=y_0\) rendimientos de la condición inicial\(y_0=ce^{ax_0}\), así\(c=y_0e^{-ax_0}\) y
\[y=y_0e^{-ax_0}e^{ax}=y_0e^{a(x-x_0)}. \nonumber\]
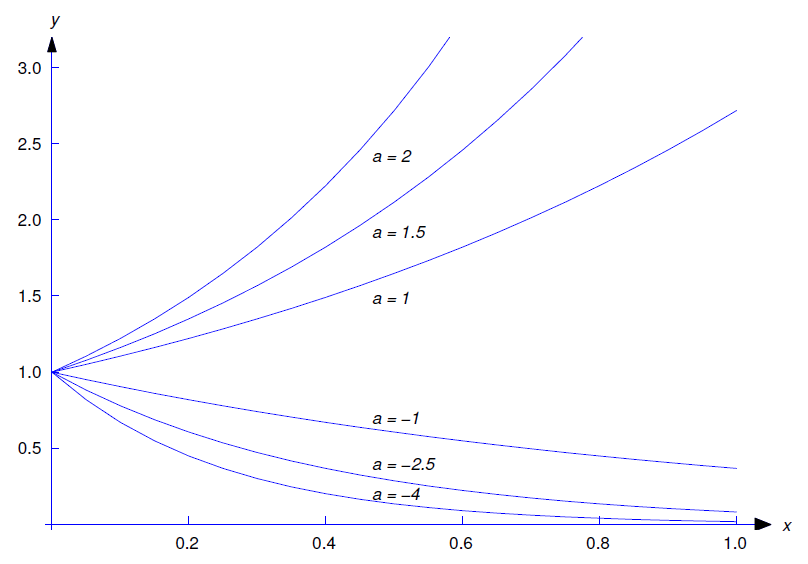
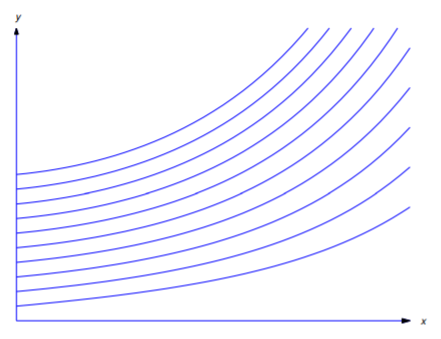
La figura 2.1.1 muestra las gráficas de esta función con\(x_{0}=0\)\(y_{0}=1\), y varios valores de\(a\).
a. Encuentre la solución general de
\[xy'+y=0.\label{eq:2.1.8}\]
b. Resolver el problema de valor inicial
\[xy'+y=0,\quad y(1)=3.\label{eq:2.1.9}\]
Solución a
Reescribimos la ecuación\ ref {eq:2.1.8} como
\[\label{eq:2.1.10} y'+{1\over x}y=0,\]
donde\(x\) se restringe a cualquiera\((-\infty,0)\) o\((0,\infty)\). Si\(y\) es una solución no trivial de la Ecuación\ ref {eq:2.1.10}, debe haber algún intervalo abierto I en el que no\(y\) tenga ceros. Podemos reescribir la ecuación\ ref {eq:2.1.10} como
\[{y'\over y}=-{1\over x} \nonumber\]
para\(x\) en\(I\). La integración demuestra que
\[\ln|y|=-\ln|x|+k,\quad so\quad|y|={e^k\over|x|}. \nonumber\]
Dado que una función que satisface la última ecuación no puede cambiar el signo en ninguno de los dos\((-\infty,0)\) o\((0,\infty)\), podemos reescribir este resultado de manera más simple como
\[\label{eq:2.1.11} y={c\over x}\]
donde
\[c=\left\{\begin{array}{cl}\phantom{-}e^k&\text{if} y>0, \\[4pt] -e^k& \,\text{if} y<0.\end{array}\right. \nonumber\]
Ahora hemos demostrado que cada solución de la Ecuación\ ref {eq:2.1.10} viene dada por la Ecuación\ ref {eq:2.1.11} para alguna elección de\(c\). (Aunque asumimos que no\(y\) era trivial derivar la Ecuación\ ref {eq:2.1.11}, podemos obtener la solución trivial estableciendo\(c=0\) en la Ecuación\ ref {eq:2.1.11}.) Por el contrario, cualquier función de la forma Ecuación\ ref {eq:2.1.11} es una solución de la Ecuación\ ref {eq:2.1.10}, ya que diferenciando la Ecuación\ ref {eq:2.1.11} rinde
\[y'=-{c\over x^2}, \nonumber\]
y sustituyendo esto y la Ecuación\ ref {eq:2.1.11} en Ecuación\ ref {eq:2.1.10} rendimientos
\[\begin{aligned} y'+{1\over x}y&=&-{c\over x^2}+{1\over x}{c\over x}\\[4pt] &=&-{c\over x^2}+{c\over x^2}=0.\end{aligned}\]
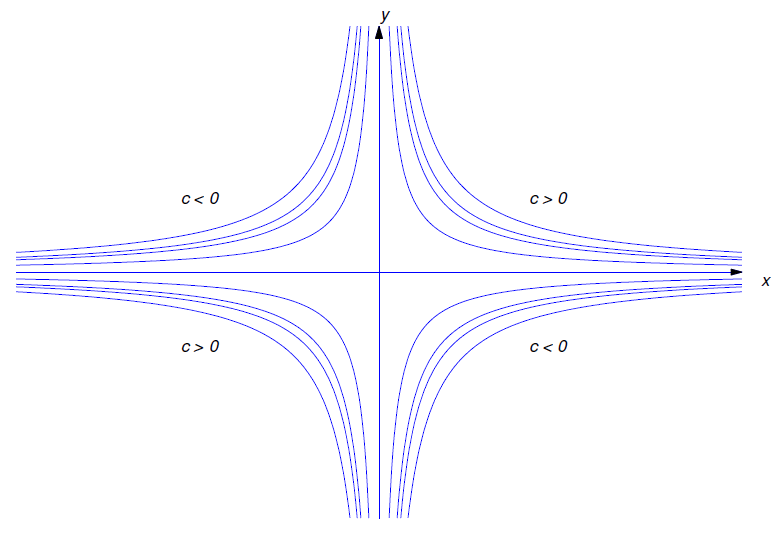
La figura 2.1.2 muestra las gráficas de algunas soluciones correspondientes a diversos valores de\(c\)
Solución b
Imponiendo la condición inicial\(y(1)=3\) en la Ecuación\ ref {eq:2.1.11} rendimientos\(c=3\). Por lo tanto, la solución de la Ecuación\ ref {eq:2.1.9} es
\[y={3\over x}. \nonumber\]
El intervalo de validez de esta solución es\((0,\infty)\).
Los resultados en Ejemplos\(\PageIndex{3a}\) y\(\PageIndex{4b}\) son casos especiales del siguiente teorema.
Si\(p\) es continuo\((a,b),\) entonces la solución general de la ecuación homogénea
\[\label{eq:2.1.12} y'+p(x)y=0\]
on\((a,b)\) es
\[y=ce^{-P(x)}, \nonumber\]
donde
\[\label{eq:2.1.13} P(x)=\int p(x)\,dx\]
es cualquier antiderivado de\(p\) sobre\((a,b);\) eso es\(,\)
\[\label{eq:2.1.15} P'(x)=p(x), \quad a<x<b\]
Si\(y=ce^{-P(x)}\), diferenciar\(y\) y usar la ecuación\ ref {eq:2.1.15} muestra que
\[y'=-P'(x)ce^{-P(x)}=-p(x)ce^{-P(x)}=-p(x)y, \nonumber\]
entonces\(y'+p(x)y=0\); es decir,\(y\) es una solución de Ecuación\ ref {eq:2.1.12}, para cualquier elección de\(c\).
Ahora vamos a mostrar que cualquier solución de la Ecuación\ ref {eq:2.1.12} se puede escribir como\(y=ce^{-P(x)}\) para alguna constante\(c\). La solución trivial se puede escribir de esta manera, con\(c=0\). Ahora supongamos que\(y\) es una solución no trivial. Después hay un subintervalo abierto\(I\) de\((a,b)\) sobre el cual no\(y\) tiene ceros. Podemos reescribir la ecuación\ ref {eq:2.1.12} como
\[\label{eq:2.1.16} \frac{y'}{y}=-p(x)\]
para\(x\) en\(I\). Integrando la ecuación\ ref {eq:2.1.16} y recordando la ecuación\ ref {eq:2.1.13} rendimientos
\[\ln|y|=-P(x) + k, \nonumber\]
donde\(k\) es una constante. Esto implica que
\[|y|=e^ke^{-P(x)}. \nonumber\]
Ya que\(P\) se define para todos\(x\) en\((a,b)\) y un exponencial nunca puede ser igual a cero, podemos tomar\(I=(a,b)\), así\(y\) tiene ceros\((a,b)\)\((a,b)\) encendidos, así podemos reescribir la última ecuación como\(y=ce^{-P(x)}\), donde
\[c=\left\{\begin{array}{cl}\phantom{-}e^k&\text{if } y>0\text{ on } (a,b),\\[4pt] -e^k&\text{if } y<0\text{ on }(a,b).\end{array}\right. \nonumber\]
OBSERVACIÓN: Reescribir una ecuación diferencial de primer orden para que un lado dependa solo de\(y\)\(y'\) y el otro dependa solo de\(x\) se llama separación de variables. Esto lo hicimos en Ejemplos 2.1.3 y 2.1.4 , y en reescribir la Ecuación\ ref {eq:2.1.12} y la Ecuación\ ref {eq:2.1.16}. Aplicaremos este método a ecuaciones no lineales en la Sección 2.2.
Ecuaciones lineales no homogéneas de primer orden
Ahora resolveremos la ecuación no homogénea
\[\label{eq:2.1.17} y'+p(x)y=f(x).\]
Al considerar esta ecuación llamamos
\[y'+p(x)y=0\nonumber \]
la ecuación complementaria.
Encontraremos soluciones de la Ecuación\ ref {eq:2.1.17} en la forma\(y=uy_1\), donde\(y_1\) es una solución no trivial de la ecuación complementaria y\(u\) está por determinar. Este método de usar una solución de la ecuación complementaria para obtener soluciones de una ecuación no homogénea es un caso especial de un método llamado variación de parámetros, que encontrarás varias veces en este libro. (Obviamente, no\(u\) puede ser constante, ya que si lo fuera, el lado izquierdo de la Ecuación\ ref {eq:2.1.17} sería cero. Reconociendo esto, los primeros usuarios de este método vieron\(u\) como un “parámetro” que varía; de ahí, el nombre “variación de parámetros”).
Si
\[y=uy_1, \quad \text{then}\quad y'=u'y_1+uy_1'.\nonumber \]
Sustituyendo estas expresiones por\(y\) y\(y'\) en Ecuación\ ref {eq:2.1.17} rinde
\[u'y_1+u(y_1'+p(x)y_1)=f(x),\nonumber \]
lo que reduce a
\[\label{eq:2.1.18} u'y_1=f(x),\]
ya que\(y_1\) es una solución de la ecuación complementaria; es decir,
\[y_1'+p(x)y_1=0.\nonumber \]
En la prueba del Teorema 2.2.1 vimos que no\(y_1\) tiene ceros en un intervalo donde\(p\) es continuo. Por lo tanto podemos dividir la Ecuación\ ref {eq:2.1.18} a través de\(y_1\) para obtener
\[u'=f(x)/y_1(x).\nonumber \]
Podemos integrar esto (introduciendo una constante de integración), y multiplicar el resultado por\(y_1\) para obtener la solución general de la Ecuación\ ref {eq:2.1.17}. Antes de pasar a la prueba formal de esta afirmación, consideremos algunos ejemplos.
Encuentre la solución general de
\[\label{eq:2.1.19} y'+2y=x^3e^{-2x}.\]
Al aplicar una de Ejemplo 2.1.3 con\(a=-2\), vemos que\(y_1=e^{-2x}\) es una solución de la ecuación complementaria\(y'+2y=0\). Por lo tanto buscamos soluciones de la Ecuación\ ref {eq:2.1.19} en la forma\(y=ue^{-2x}\), para que
\[\label{eq:2.1.20} y'=u'e^{-2x}-2ue^{-2x}\quad \text{and} \quad y'+2y=u'e^{-2x}-2ue^{-2x}+2ue^{-2x}=u'e^{-2x}.\]
Por lo tanto\(y\) es una solución de la Ecuación\ ref {eq:2.1.19} si y solo si
\[u'e^{-2x}=x^3e^{-2x}\quad \text{or, equivalently},\quad u'=x^3.\nonumber \]
Por lo tanto
\[u={x^4\over4}+c,\nonumber \]
y
\[y=ue^{-2x}=e^{-2x}\left({x^4\over4}+c\right)\nonumber \]
es la solución general de la Ecuación\ ref {eq:2.1.19}.
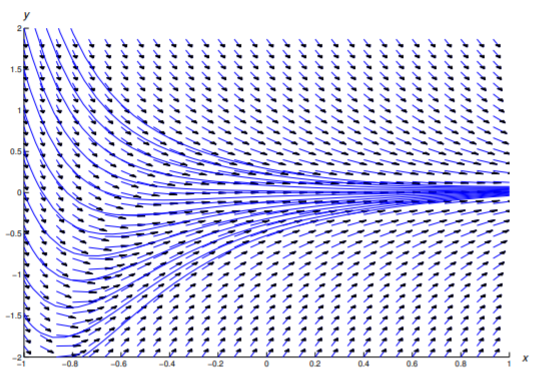
La Figura 2.1.3 muestra un campo de dirección y algunas curvas integrales para la Ecuación\ ref {eq:2.1.19}.
Encuentre la solución general
\[\label{eq:2.1.29} y'+(\cot x)y=x\csc x.\]
Resolver el problema de valor inicial
\[\label{eq:2.1.30} y'+(\cot x)y=x\csc x,\quad y(\pi/2)=1.\]
Aquí\(p(x)=\cot x\) y ambos\(f(x)= x\csc x\) son continuos excepto en los puntos\(x=r\pi\), donde\(r\) es un entero. Por lo tanto buscamos soluciones de Ecuación\ ref {eq:2.1.29} en los intervalos\(\left(r\pi, (r+1)\pi \right)\). Necesitamos una solución no trival\(y_1\) de la ecuación complementaria; así,\(y_1\) debemos satisfacer\(y_1'+(\cot x)y_1=0\), que reescribimos como
\[\label{eq:2.1.22} {y_1'\over y_1}=-\cot x=-{\cos x\over\sin x}.\]
Integrando estos rendimientos
\[\ln|y_1|=-\ln|\sin x|,\nonumber \]
donde tomamos la constante de integración para ser cero ya que necesitamos solo una función que satisfaga la Ecuación\ ref {eq:2.1.22}. Claramente\(y_1=1/\sin x\) es una opción adecuada. Por lo tanto buscamos soluciones de Ecuación\ ref {eq:2.1.29} en la forma
\[y={u\over\sin x},\nonumber \]
para que
\[\label{eq:2.1.23} y'={u'\over\sin x}-{u\cos x\over\sin^2x}\]
y
\[\label{eq:2.1.24} \begin{array}{rcl} y'+(\cot x)y&=& {u'\over\sin x}-{u\cos x\over\sin^2x}+{u\cot x\over\sin x}\\[4pt] &=&{u'\over\sin x}-{u\cos x\over\sin^2x}+{u\cos x\over\sin^2 x}\\[4pt] &=&{u'\over\sin x}. \end{array}\]
Por lo tanto\(y\) es una solución de la Ecuación\ ref {eq:2.1.29} si y solo si
\[u'/\sin x=x\csc x=x/\sin x\quad \text{or, equivalently,}\quad u'=x.\nonumber \]
Integrando estos rendimientos
\[\label{eq:2.1.25} u={x^2\over2}+c, \quad\text{ and}\quad y={u\over\sin x}= {x^2\over 2\sin x}+ {c\over\sin x}.\]
es la solución general de la Ecuación\ ref {eq:2.1.29} en cada intervalo\(\left(r\pi,(r+1)\pi\right)\) (\(r=\)entero).
b. Imponer la condición inicial\(y(\pi/2)=1\) en la ecuación\ ref {eq:2.1.25} rendimientos
\[1={\pi^2\over 8}+c\text{ or} c=1-{\pi^2\over 8}.\nonumber \]
Por lo tanto,
\[y={x^2\over 2\sin x}+{(1-\pi^2/8)\over\sin x}\nonumber \]
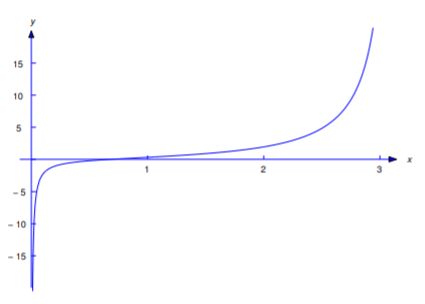
es una solución de la Ecuación\ ref {eq:2.1.29}. El intervalo de validez de esta solución es\((0,\pi)\); la Figura 2.1.4 muestra su gráfica.
OBSERVACIÓN: No fue necesario hacer los cálculos\ ref {eq:2.1.23} y\ ref {eq:2.1.24} en Ejemplo 2.1.6 , ya que mostramos en la discusión anterior al Ejemplo 2.1.5 que si\(y = uy_{1}\) donde\(y'_{1}+ p(x)y_{1}=0\), entonces\(y'+ p(x)y = u'y_{1}\). Hicimos estos cómputos para que veas que esto sucediera en este ejemplo específico. Te recomendamos que incluyas estos cálculos “innecesarios” en la realización de ejercicios, hasta que estés seguro de que realmente entiendes el método. Después de eso, omítelos.
Resumimos el método de variación de parámetros para resolver
\[\label{eq:2.1.26} y'+p(x)y=f(x)\]
de la siguiente manera:
a. Encontrar una función\(y_1\) tal que
\[{y_1'\over y_1}=-p(x).\nonumber \]
Para mayor comodidad, tome la constante de integración para ser cero.
b. Escribir
\[\label{eq:2.1.27} y=uy_1\]
para recordarte lo que estás haciendo.
c. Escribir\(u'y_1=f\) y resolver para\(u'\); así,\(u'=f/y_1\).
d.\(u'\) Integrar para obtener\(u\), con una constante arbitraria de integración.
e. Sustituir\(u\) en la Ecuación\ ref {eq:2.1.27} para obtener\(y\).
Para resolver una ecuación escrita como
\[P_0(x)y'+P_1(x)y=F(x),\nonumber \]
te recomendamos que dividas por\(P_0(x)\) para obtener una ecuación de la forma Ecuación\ ref {eq:2.1.26} y luego seguir este procedimiento.
Soluciones en Forma Integral
En ocasiones las integrales que surgen al resolver una ecuación lineal de primer orden no pueden ser evaluadas en términos de funciones elementales. En este caso la solución debe dejarse en términos de una integral.
Encuentre la solución general de
\[y'-2xy=1.\nonumber \]
Resolver el problema de valor inicial
\[\label{eq:2.1.28} y'-2xy=1,\quad y(0)=y_0.\]
a. Para aplicar variación de parámetros, necesitamos una solución no trivial\(y_1\) de la ecuación complementaria; así,\(y_1'-2xy_1=0\), que reescribimos como
\[{y_1'\over y_1}=2x.\nonumber \]
Integrando esto y tomando la constante de integración para ser cero rendimientos
\[\ln|y_1|=x^2,\quad \text{so} \quad|y_1|=e^{x^2}.\nonumber \]
Elegimos\(y_1=e^{x^2}\) y buscamos soluciones de Ecuación\ ref {eq:2.1.28} en la forma\(y=ue^{x^2}\), donde
\[u'e^{x^2}=1,\quad \text{so} \quad u'=e^{-x^2}.\nonumber \]
Por lo tanto
\[u=c+\int e^{-x^2}dx,\nonumber \]
pero no podemos simplificar la integral a la derecha porque no hay una función elemental con derivada igual a\(e^{-x^2}\). Por lo tanto, la mejor forma disponible para la solución general de la Ecuación\ ref {eq:2.1.28} es
\[\label{eq:2.1.49}y=ue^{x^2}= e^{x^2}\left(c+\int e^{-x^2}dx\right).\]
b. Dado que la condición inicial en la Ecuación\ ref {eq:2.1.28} se impone en\(x_0=0\), es conveniente reescribir la Ecuación\ ref {eq:2.1.49} como
\[\begin{aligned}y=e^{x^2}\left(c+\int_{0}^{x}e^{-t^2}dt \right), \quad\text{since}\quad\int_{0}^{0}e^{-t^2}dt=0\end{aligned}\nonumber \]
Ambientación\(x=0\) y\(y=y_0\) aquí lo demuestra\(c=y_0\). Por lo tanto, la solución del problema de valor inicial es
\[\label{eq:2.1.51}y=e^{x^2}\left(y_0 +\int^x_0 e^{-t^2}dt\right).\]
Para un valor dado de\(y_0\) y cada uno fijo\(x\), la integral de la derecha puede ser evaluada por métodos numéricos. Un procedimiento alternativo es aplicar los procedimientos de integración numérica discutidos en el Capítulo 3 directamente al problema del valor inicial Ecuación\ ref {eq:2.1.28}. La Figura 2.1.5 muestra gráficas de la Ecuación\ ref {eq:2.1.51} para varios valores de\(y_0\).
Un teorema de existencia y singularidad
El método de variación de parámetros conduce a este teorema.
Supongamos\(p\) y\(f\) son continuos en un intervalo abierto\((a,b),\) y dejar que\(y_1\) sea cualquier solución no trivial de la ecuación complementaria
\[y'+p(x)y=0 \nonumber\]
encendido\((a,b)\). Entonces:
- La solución general de la ecuación\[\label{eq:2.1.31} y'+p(x)y=f(x)\] no homogénea\((a,b)\) es\[\label{eq:2.1.32} y=y_1(x)\left(c +\int f(x)/y_1(x)\,dx\right).\]
- Si\(x_0\) es un punto arbitrario\((a,b)\) y\(y_0\) es un número real arbitrario\(,\) entonces el problema del valor inicial\[y'+p(x)y=f(x),\quad y(x_0)=y_0\nonumber \] tiene la solución única\[ y=y_1(x)\left({y_0\over y_1(x_0)} +\int^x_{x_0} {f(t)\over y_1(t)}\, dt\right)\nonumber \] en\((a,b).\)
- Prueba
-
(a) Para mostrar que la Ecuación\ ref {eq:2.1.32} es la solución general de la Ecuación\ ref {eq:2.1.31} on\((a,b)\), debemos probar que:
- Si\(c\) es alguna constante, la función\(y\) en la Ecuación\ ref {eq:2.1.32} es una solución de la Ecuación\ ref {eq:2.1.31} on\((a,b)\).
- Si\(y\) es una solución de la Ecuación\ ref {eq:2.1.31} on\((a,b)\) entonces\(y\) es de la forma Ecuación\ ref {eq:2.1.32} para alguna constante\(c\).
Para probar (i), primero observamos que cualquier función de la forma Ecuación\ ref {eq:2.1.32} se define on\((a,b)\), ya que\(p\) y\(f\) son continuas en\((a,b)\). Ecuación diferenciadora\ ref {eq:2.1.32} rendimientos
\[y'=y_1'(x)\left(c +\int f(x)/y_1(x)\, dx\right)+f(x).\nonumber \]
Ya que\(y_1'=-p(x)y_1\), esto y la Ecuación\ ref {eq:2.1.32} implican que
\[\begin{aligned} y'&=-p(x)y_1(x)\left(c +\int f(x)/y_1(x)\, dx\right)+f(x)\\[4pt] &=-p(x)y(x)+f(x),\end{aligned}\nonumber \]
lo que implica que\(y\) es una solución de la Ecuación\ ref {eq:2.1.31}.
Para probar (ii), supongamos que\(y\) es una solución de la Ecuación\ ref {eq:2.1.31} on\((a,b)\). A partir de la prueba del Teorema 2.1.1, sabemos que no\(y_1\) tiene ceros encendidos\((a,b)\), por lo que la función\(u=y/y_1\) se define en\((a,b)\). Además, desde
\[y'=-py+f\quad \text{and}\quad y_1'=-py_1,\nonumber \]
\[\begin{aligned} u'&={y_1y'-y_1'y\over y_1^2} \\[4pt] &={y_1(-py+f)-(-py_1)y\over y_1^2}={f\over y_1}.\end{aligned}\nonumber \]
Integración de\(u'=f/y_1\) rendimientos
\[u=\left(c +\int f(x)/y_1(x)\, dx\right),\nonumber \]
lo que implica Ecuación\ ref {eq:2.1.32}, ya que\(y=uy_1\).
(b) Hemos probado (a), donde\(\int f(x)/y_1(x)\,dx\) en la Ecuación\ ref {eq:2.1.32} es una antiderivada arbitraria de\(f/y_1\). Ahora es conveniente elegir la antiderivada que equivale a cero cuando\(x=x_0\), y escribir la solución general de la Ecuación\ ref {eq:2.1.31} como
\[y=y_1(x)\left(c +\int^x_{x_0} {f(t)\over y_1(t)}\, dt\right). \nonumber\]
Desde
\[y(x_0)= y_1(x_0)\left(c +\int^{x_0}_{x_0} {f(t)\over y_1(t)}\, dt\right)=cy_1(x_0), \nonumber\]
vemos que\(y(x_0)=y_0\) si y solo si\(c=y_0/y_1(x_0)\).


