6.2: Problemas de Primavera II

Vibraciones libres con amortiguación

En esta sección consideramos el movimiento de un objeto en un sistema de muelle—masa con amortiguación. Comenzamos con el movimiento no forzado, por lo que la ecuación del movimiento es

\[\label{eq:6.2.1} my''+cy'+ky=0.\]

Ahora supongamos que el objeto se desplaza del equilibrio y se le da una velocidad inicial. La intuición sugiere que si la fuerza de amortiguación es suficientemente débil el movimiento resultante será oscilatorio, como en el caso no amortiguado considerado en la sección anterior, mientras que si es suficientemente fuerte el objeto puede simplemente moverse lentamente hacia la posición de equilibrio sin llegar nunca a ella. Ahora confirmaremos matemáticamente estas ideas intuitivas. La ecuación característica de la ecuación\ ref {eq:6.2.1} es

\[mr^2+cr+k=0. \nonumber \]

Las raíces de esta ecuación son

\[\label{eq:6.2.2} r_1={-c-\sqrt{c^2-4mk}\over2m}\quad \text{and} \quad r_2= {-c+\sqrt{c^2-4mk}\over2m}.\]

Vimos en la Sección 5.2 que la forma de la solución de la Ecuación\ ref {eq:6.2.1} depende de si\(c^2-4mk\) es positiva, negativa o cero. Ahora consideraremos estos tres casos.

Movimiento subamortiguado

Decimos que la moción está subamortiguada si\(c<\sqrt{4mk}\). En este caso\(r_1\) y\(r_2\) en la Ecuación\ ref {eq:6.2.2} son conjugados complejos, los cuales escribimos como

\[r_1=-{c\over2m}-\omega_1\,i\quad \text{and} \quad r_2=-{c\over2m}+\omega_1\,i, \nonumber \]

donde

\[\omega_1={\sqrt{4mk-c^2}\over2m}. \nonumber \]

La solución general de la Ecuación\ ref {eq:6.2.1} en este caso es

\[y=e^{-ct/2m}(c_1\cos\omega_1 t+c_2\sin\omega_1 t). \nonumber \]

Por el método utilizado en la Sección 6.1 para derivar la forma amplitude-fase del desplazamiento de un objeto en simple movimiento armónico, podemos reescribir esta ecuación como

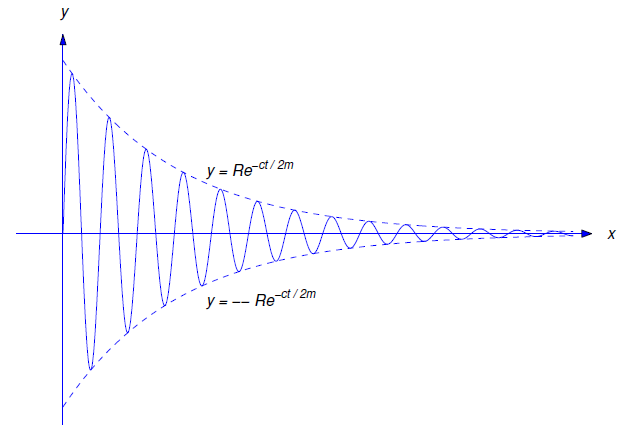
\[\label{eq:6.2.3} y=Re^{-ct/2m}\cos(\omega_1 t-\phi),\]

Figura 6.2.1 : Movimiento subamortiguado

donde

\[R=\sqrt{c_1^2+c_2^2},\quad R\cos\phi=c_1,\quad \text{and} \quad R\sin\phi=c_2. \nonumber \]

El factor\(Re^{-ct/2m}\) en la Ecuación\ ref {eq:6.2.3} se llama el tiempo—amplitud variable del movimiento, la cantidad\(\omega_1\) se llama la frecuencia, y\(T=2\pi/\omega_1\) (que es el período de la función coseno en la Ecuación\ ref {eq:6.2.3} se llama cuasi-período. Un gráfico típico de la Ecuación\ ref {eq:6.2.3} se muestra en la Figura 6.2.1 . Como se ilustra en esa figura, la gráfica de\(y\) oscila entre las curvas exponenciales discontinuas\(y=\pm Re^{-ct/2m}\).

Movimiento sobreamortiguado

Decimos que la moción está sobreamortiguada si\(c>\sqrt{4mk}\). En este caso los ceros\(r_1\) y\(r_2\) del polinomio característico son reales, con\(r_1 <r_{2}<0\) (ver\ ref {eq:6.2.2}), y la solución general de\ ref {eq:6.2.1} es

\[y=c_1e^{r_1t}+c_2e^{r_2t}. \nonumber \]

Nuevamente\(\lim_{t\to\infty}y(t)=0\) como en el caso subamortiguado, pero el movimiento no es oscilatorio, ya que no\(y\) puede ser igual a cero por más de un valor de\(t\) a menos\(c_1=c_2=0\). (Ejercicio 6.2.23.)

Movimiento críticamente amortiguado

Decimos que el movimiento está críticamente amortiguado si\(c=\sqrt{4mk}\). En este caso\(r_1=r_2=-c/2m\) y la solución general de la Ecuación\ ref {eq:6.2.1} es

\[y=e^{-ct/2m}(c_1+c_2t). \nonumber \]

Nuevamente\(\lim_{t\to\infty}y(t)=0\) y el movimiento es no oscilatorio, ya que no\(y\) puede ser igual a cero por más de un valor de\(t\) a menos\(c_1=c_2=0\). (Ejercicio 6.2.22).

Ejemplo 6.2.1

Supongamos que un peso de\(64\) lb estira un resorte\(6\) pulgadas en equilibrio y un amortiguador proporciona una fuerza de amortiguación de\(c\) lb por cada pies/seg de velocidad.

1. Escribe la ecuación de movimiento del objeto y determina el valor\(c\) para el cual el movimiento está amortiguado críticamente.
2. Encuentre el desplazamiento\(y\) para\(t>0\) si el movimiento está amortiguado críticamente y las condiciones iniciales son\(y(0)=1\) y\(y'(0)=20\).
3. Encuentre el desplazamiento\(y\) para\(t>0\) si el movimiento está amortiguado críticamente y las condiciones iniciales son\(y(0)=1\) y\(y'(0)=-20\).

Solución a

Aquí\(m=2\) babosas y\(k=64/.5=128\) lb/ft. Por lo tanto, la ecuación de movimiento Ecuación\ ref {eq:6.2.1} es

\[\label{eq:6.2.4} 2y''+cy'+128y=0.\]

La ecuación característica es

\[2r^2+cr+128=0, \nonumber \]

que tiene raíces

\[r={-c\pm\sqrt{c^2-8\cdot128}\over4}. \nonumber \]

Por lo tanto, la amortiguación es crítica si

\[c=\sqrt{8\cdot128}=32\mbox{ lb-sec/ft}. \nonumber \]

Solución b

Establecer\(c=32\) en la ecuación\ ref {eq:6.2.4} y cancelar los\(2\) rendimientos del factor común

\[y''+16y+64y=0. \nonumber\]

La ecuación característica es

\[r^2+16r+64y=(r+8)^2=0. \nonumber\]

Por lo tanto, la solución general es

\[\label{eq:6.2.5} y=e^{-8t}(c_1+c_2t).\]

Figura 6.2.2 : (a)\(y=e^{-8t}(1+28t)\) y (b)\(y=e^{-8t}(1-12t)\)

Diferenciando estos rendimientos

\[\label{eq:6.2.6} y'=-8y+c_2e^{-8t}.\]

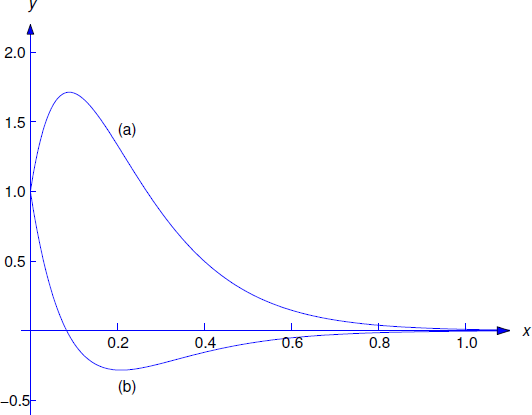
6.2.2 La imposición de las condiciones iniciales\(y(0)=1\) y\(y'(0)=20\) en las dos últimas ecuaciones muestra que\(1=c_1\) y\(20=-8+c_2\). De ahí que la solución del problema del valor inicial sea

\[y=e^{-8t}(1+28t). \nonumber \]

Por lo tanto el objeto se acerca al equilibrio desde arriba como\(t\to\infty\). No hay oscilación.

Solución c

Imponiendo las condiciones iniciales\(y(0)=1\) y\(y'(0)=-20\) en Ecuación\ ref {eq:6.2.5} y Ecuación\ ref {eq:6.2.6} rendimientos\(1=c_1\) y\(-20=-8+c_2\). De ahí que la solución de este problema de valor inicial sea

\[y=e^{-8t}(1-12t). \nonumber \]

Por lo tanto el objeto se mueve hacia abajo a través del equilibrio solo una vez, y luego se acerca al equilibrio desde abajo como\(t\to\infty\) Nuevamente, no hay oscilación. Las soluciones de estos dos problemas de valor inicial se grafican en la Figura 6.2.2 .

Ejemplo 6.2.2

Encuentre el desplazamiento del objeto en el Ejemplo 6.2.1 si la constante de amortiguación es\(c=4\) lb—seg/ft y las condiciones iniciales son\(y(0)=1.5\) ft y\(y'(0)=-3\) ft/seg.

Solución

Con\(c=4\), la ecuación de movimiento Ecuación\ ref {eq:6.2.4} se convierte

\[\label{eq:6.2.7} y''+2y'+64y=0\]

después de cancelar el factor común 2. La ecuación característica

\[r^2+2r+64=0 \nonumber\]

tiene raíces conjugadas complejas

\[r={-2\pm\sqrt{4-4\cdot64}\over2}=-1\pm3\sqrt7i. \nonumber\]

Por lo tanto, el movimiento está subamortiguado y la solución general de la Ecuación\ ref {eq:6.2.7} es

\[y=e^{-t}(c_1\cos3\sqrt7t+c_2\sin3\sqrt7t). \nonumber\]

Diferenciando estos rendimientos

\[y'=-y+3\sqrt7e^{-t}(-c_1\sin3\sqrt7t+c_2\cos3\sqrt7t). \nonumber\]

Imponer las condiciones iniciales\(y(0)=1.5\) y\(y'(0)=-3\) en las dos últimas ecuaciones rinde\(1.5=c_1\) y\(-3=-1.5+3\sqrt7c_2\). De ahí que la solución del problema del valor inicial sea

\[\label{eq:6.2.8} y=e^{-t}\left({3\over2}\cos3\sqrt7t-{1\over2\sqrt7} \sin3\sqrt7t\right).\]

La amplitud de la función entre paréntesis es

\[R=\sqrt{\left(\frac{3}{2} \right)^{2}+\left(\frac{1}{2\sqrt{7}} \right)^{2}}=\sqrt{\frac{9}{4}+\frac{1}{4\cdot 7}}=\sqrt{\frac{64}{4\cdot 7}}=\frac{4}{\sqrt{7}} \nonumber\]

Por lo tanto podemos reescribir la Ecuación\ ref {eq:6.2.8} como

\[y={4\over\sqrt7}e^{-t}\cos(3\sqrt7t-\phi), \nonumber\]

donde

\[\cos\phi={3\over2R}={3\sqrt7\over8}\quad \text{and} \quad\sin\phi=-{1\over2\sqrt7R}= -{1\over8}. \nonumber\]

Por lo tanto\(\phi \cong -0.125\) radianes.

Ejemplo 6.2.3

Deje que la constante de amortiguación en el Ejemplo 6.2.1 sea\(c=40\) lb—seg/ft. Encuentra el desplazamiento\(y\) para\(t>0\) si\(y(0)=1\) y\(y'(0)=1\).

Solución

Con\(c=40\), la ecuación de movimiento Ecuación\ ref {eq:6.2.4} se reduce a

\[\label{eq:6.2.9} y''+20y'+64y=0\]

después de cancelar el factor común 2. La ecuación característica

\[r^2+20r+64=(r+16)(r+4)=0 \nonumber\]

tiene las raíces\(r_1=-4\) y\(r_2=-16\). Por lo tanto, la solución general de la Ecuación\ ref {eq:6.2.9} es

\[\label{eq:6.2.10} y=c_1e^{-4t}+c_2e^{-16t}.\]

Diferenciando estos rendimientos

\[y'=-4e^{-4t}-16c_2e^{-16t}. \nonumber\]

Figura 6.2.3 : \(y={17\over12}e^{-4t}-{5\over12}e^{-16t}\)

Las dos últimas ecuaciones y las condiciones iniciales\(y(0)=1\) e\(y'(0)=1\) implican que

\[\begin{array}{rlrl} c_1&+&c_2&=1\\ -4c_1&-&16c_2&=1. \end{array} \nonumber\]

La solución de este sistema es\(c_1=17/12\),\(c_2=-5/12\). Sustituyendo estos en Ecuación\ ref {eq:6.2.10} rendimientos

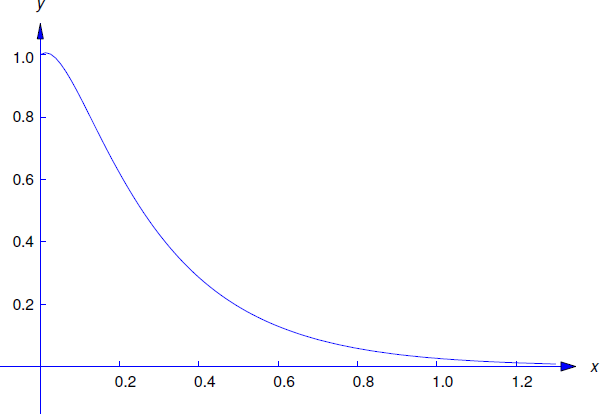
\[y={17\over12}e^{-4t}-{5\over12}e^{-16t} \nonumber\]

como la solución del problema de valor inicial dado (Figura 6.2.3 ).

Vibraciones forzadas con amortiguación

Ahora consideramos el movimiento de un objeto en un sistema de masa-resorte con amortiguación, bajo la influencia de una función de forzamiento periódico\(F(t)=F_0\cos\omega t\), de manera que la ecuación de movimiento es

\[\label{eq:6.2.11} my''+cy'+ky=F_0\cos\omega t.\]

En la Sección 6.1 consideramos esta ecuación con\(c=0\) y encontramos que el desplazamiento resultante\(y\) asumió valores arbitrariamente grandes en el caso de la resonancia (es decir, cuándo\(\omega=\omega_0=\sqrt{k/m}\)). Aquí veremos que ante la presencia de amortiguación el desplazamiento permanece acotado para todos\(t\), y las condiciones iniciales tienen poco efecto sobre el movimiento como\(t\to\infty\). De hecho, veremos que para grandes\(t\) el desplazamiento se aproxima de cerca por una función de la forma

\[\label{eq:6.2.12} y=R\cos(\omega t-\phi),\]

donde la amplitud\(R\) depende de\(m\),\(c\),\(k\),\(F_0\), y\(\omega\). Nos interesa la siguiente pregunta:

Pregunta

Suponiendo que\(m\)\(c\),\(k\), y\(F_0\) se mantienen constantes, ¿qué valor de\(\omega\) produce la mayor amplitud\(R\) en la Ecuación\ ref {eq:6.2.12}, y cuál es esta mayor amplitud?

Para responder a esta pregunta, debemos resolver la Ecuación\ ref {eq:6.2.11} y determinar\(R\) en términos de\(F_0,\omega_0,\omega\), y\(c\). Podemos obtener una solución particular de la Ecuación\ ref {eq:6.2.11} por el método de coeficientes indeterminados. Dado que\(\cos\omega t\) no satisface la ecuación complementaria

\[my''+cy'+ky=0, \nonumber \]

podemos obtener una solución particular de la Ecuación\ ref {eq:6.2.11} en la forma

\[\label{eq:6.2.13} y_p=A\cos\omega t+B\sin\omega t.\]

Diferenciando estos rendimientos

\[y_p'=\quad\omega (-A\sin\omega t+B\cos\omega t) \nonumber \]

y

\[y_p''=-\omega^2(A\cos\omega t+B\sin\omega t). \nonumber \]

De las tres últimas ecuaciones,

\[my''_p+cy'_p+ky_p=(-m\omega^2A+c\omega B+kA)\cos\omega t+ (-m\omega^2 B-c\omega A+kB)\sin\omega t, \nonumber \]

así\(y_p\) satisface la Ecuación\ ref {eq:6.2.11} si

\[\begin{array}{lll} (k-m\omega^2) A+\quad c\omega B &=F_0\\ -c\omega A\quad+(k-m\omega^2)B&= 0. \end{array} \nonumber \]

Resolviendo\(A\)\(B\) y sustituyendo los resultados en Ecuación\ ref {eq:6.2.13} rendimientos

\[y_p={F_0\over(k-m\omega^2)^2+c^2\omega^2} \left[(k-m\omega^2)\cos\omega t+c\omega\sin\omega t\right], \nonumber \]

que se puede escribir en forma de amplitud—fase como

\[\label{eq:6.2.14} %\springsteady y_p={F_0\over\sqrt{(k-m\omega^2)^2+c^2\omega^2}} \cos(\omega t-\phi),\]

donde

\[\label{eq:6.2.15} \cos\phi={k-m\omega^2\over\sqrt {(k-m\omega^2)^2+c^2\omega^2}}\quad \text{and} \quad \sin\phi={c\omega\over\sqrt{(k-m\omega^2)^2+c^2\omega^2}}.\]

Para comparar esto con la vibración forzada no amortiguada que consideramos en la Sección 6.1 es útil escribir

\[\label{eq:6.2.16} k-m\omega^2=m\left({k\over m}-\omega^2\right)= m(\omega_0^2-\omega^2),\]

donde\(\omega_0=\sqrt{k/m}\) es la frecuencia angular natural del movimiento armónico simple sin amortiguar de un objeto con masa\(m\) en un resorte con constante\(k\). Sustituyendo la ecuación\ ref {eq:6.2.16} en Ecuación\ ref {eq:6.2.14} rendimientos

\[\label{eq:6.2.17} y_p={F_0\over\sqrt{m^2(\omega^2_0-\omega^2)^2+ c^2\omega^2}}\cos(\omega t-\phi).\]

La solución de un problema de valor inicial

\[my''+cy'+ky=F_0\cos\omega t, \quad y(0)=y_0,\quad y'(0)=v_0, \nonumber \]

es de la forma\(y=y_c+y_p\), donde\(y_c\) tiene una de las tres formas

\[\begin{aligned} y_c&= e^{-ct/2m}(c_1\cos\omega_1t+c_2\sin\omega_1t),\\ y_c&= e^{-ct/2m}(c_1+c_2t),\\ y_c&= c_1e^{r_1t}+c_2e^{r_2t}\,(r_1,r_2<0).\end{aligned} \nonumber \]

En los tres casos\(\displaystyle \lim_{t\to\infty} y_c(t)=0\) para cualquier elección de\(c_1\) y\(c_2\). Por esta razón decimos que\(y_c\) es el componente transitorio de la solución\(y\). El comportamiento de\(y\) para grandes\(t\) está determinado por\(y_p\), que llamamos el componente de estado estacionario de\(y\). Así, para grandes\(t\) el movimiento es como simple movimiento armónico a la frecuencia de la fuerza externa.

La amplitud de\(y_p\) en la Ecuación\ ref {eq:6.2.17} es

\[\label{eq:6.2.18} R={F_0\over\sqrt{m^2(\omega^2_0-\omega^2)^2+c^2\omega^2}},\]

que es finito para todos\(\omega\); es decir, la presencia de amortiguamiento impide el fenómeno de resonancia que encontramos al estudiar las vibraciones sin amortiguar bajo una función de forzamiento periódico. Ahora encontraremos el valor\(\omega\) para\(\omega_{\max}\) el cual\(R\) se maximiza. Este es el valor\(\omega\) para el cual la función

\[\rho (\omega)=m^2(\omega^2_0-\omega^2)^2+c^2\omega^2 \nonumber \]

en el denominador de la Ecuación\ ref {eq:6.2.18} alcanza su valor mínimo. Al reescribir esto como

\[\label{eq:6.2.19} \rho (\omega)=m^2(\omega^4_0+\omega^4)+ (c^2-2m^2\omega^2_0)\omega^2,\]

se puede ver que\(\rho\) es una función estrictamente creciente de\(\omega^2\) si

\[c\ge\sqrt{2m^2\omega^2_0}=\sqrt{2mk}. \nonumber \]

(Recordemos eso\(\omega^2_0=k/m\)). Por lo tanto,\(\omega_{\max}=0\) si esta desigualdad se mantiene. De la Ecuación\ ref {eq:6.2.15}, se puede ver que\(\phi=0\) si\(\omega=0\). En este caso, la Ecuación\ ref {eq:6.2.14} reduce a

\[y_p={F_0\over\sqrt{m^2\omega^4_0}}={F_0\over k}, \nonumber \]

lo cual es congruente con la ley de Hooke: si la masa es sometida a una fuerza constante\(F_0\), su desplazamiento debe acercarse a una constante\(y_p\) tal que\(ky_p=F_0\). Ahora supongamos\(c<\sqrt{2mk}\). Entonces, de la Ecuación\ ref {eq:6.2.19},

\[\rho'(\omega)=2\omega(2m^2\omega^2+c^2-2m^2\omega^2_0), \nonumber \]

y\(\omega_{\max}\) es el valor\(\omega\) para el cual la expresión entre paréntesis es igual a cero; es decir,

\[\omega_{\max}=\sqrt{\omega^2_0-{c^2\over2m^2}} =\sqrt{{k\over m}\left(1-{c^2\over2km}\right)}. \nonumber \]

(Para ver que\(\rho(\omega_{\max})\) es el valor mínimo de\(\rho(\omega)\), tenga en cuenta que\(\rho'(\omega)<0\) si\(\omega <\omega_{\max}\) y\(\rho'(\omega)>0\) si\(\omega>\omega_{\max}\).) Sustituir\(\omega=\omega_{\max}\) en la ecuación\ ref {eq:6.2.18} y simplificar muestra que la amplitud máxima\(R_{\max}\) es

\[R_{\max}={2mF_0\over c\sqrt{4mk-c^2}} \quad \text{if} \quad c< \sqrt{2mk}. \nonumber \]

Resumimos nuestros resultados de la siguiente manera.

Teorema 6.2.1

Supongamos que consideramos la amplitud\(R\) del componente de estado estacionario de la solución de

\[my''+cy'+ky=F_0\cos\omega t \nonumber\]

en función de\(\omega\).

1. Si\(c\ge\sqrt{2mk}\), la amplitud máxima es\(R_{\max}=F_0/k\) y se alcanza cuando\(\omega= \omega_{\max}=0\).
2. Si\(c<\sqrt{2mk}\), la amplitud máxima es

\[\label{eq:6.2.20} R_{\max}={2m F_0\over c\sqrt{4mk-c^2}},\]

y se logra cuando

\[\label{eq:6.2.21} \omega=\omega_{\max}=\sqrt{{k\over m}\left(1-{c^2\over 2km}\right)}.\]

Tenga en cuenta que\(R_{\max}\) y\(\omega_{\max}\) son funciones continuas de\(c\), para\(c\ge0\), desde Ecuación\ ref {eq:6.2.20} y Ecuación\ ref {eq:6.2.21} reducir a\(R_{\max}=F_0/k\) y\(\omega_{\max}=0\) si\(c=\sqrt{2km}\).