6.4E: Movimiento bajo una fuerza central (Ejercicios)

Q6.4.1

1. Encuentra la ecuación de la curva

\[r={\rho\over 1+e\cos(\theta-\phi)} \tag{A}\]

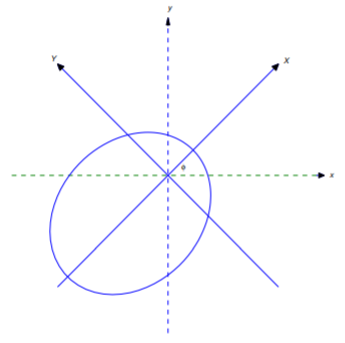
en términos de\((X,Y)=\left(r\cos(\theta-\phi),r\sin(\theta-\phi)\right)\), que son coordenadas rectangulares con respecto a los ejes mostrados en la Figura 6.4E.1 . Usa tus resultados para verificar que (A) es la ecuación de una elipse si\(0<e<1\), una parábola si\(e=1\), o una hipérbola si\(e>1\). Si\(e<1\), deja tu respuesta en el formulario

\[{(X-X_0)^2\over a^2}+{(Y-Y_0)^2\over b^2}=1,\]

y mostrar que el área de la elipse es

\[A={\pi\rho^2\over(1-e^2)^{3/2}}.\]

Luego use el Teorema 6.4.1 para mostrar que el tiempo requerido para que el objeto atraviese toda la órbita es

\[T={2\pi\rho^2\over h(1-e^2)^{3/2}}.\]

(Esta es la tercera ley de Kepler;\(T\) se llama el período de la órbita).

Figura 6.4E.1

2. Supongamos que un objeto con masa\(m\) se mueve en el\(xy\) plano bajo la fuerza central

\[{\bf F}(r,\theta)=-{mk\over r^2}(\cos\theta\,{\bf i}+\sin\theta\,{\bf j}),\]

donde\(k\) es una constante positiva. Como mostramos, la órbita del objeto viene dada por

\[r={\rho\over 1+e\cos(\theta-\phi)}.\]

Determinar\(\rho\)\(e\),, y\(\phi\) en términos de las condiciones iniciales

\[r(0)=r_0,\quad r'(0)=r_0', \quad\text{and}\quad \theta(0)=\theta_0,\quad \theta'(0)=\theta_0'.\]

Supongamos que los vectores de posición y velocidad iniciales no son colineales.

3. Supongamos que deseamos poner un satélite con masa\(m\) en una órbita elíptica alrededor de la Tierra. Supongamos que la única fuerza que actúa sobre el objeto es la gravedad de la Tierra, dada por

\[{\bf F}(r,\theta)=-mg\left(R^2\over r^2\right)(\cos\theta\,{\bf i}+\sin\theta\,{\bf j}),\]

donde\(R\) está el radio de la Tierra,\(g\) es la aceleración debida a la gravedad en la superficie de la Tierra,\(r\) y\(\theta\) son coordenadas polares en el plano de la órbita, con el origen en el centro de la Tierra.

1. Encontrar la excentricidad requerida para hacer que las distancias de afelio y perihelio sean iguales a\(R\gamma_1\) y\(R\gamma_2\), respectivamente, dónde\(1<\gamma_1<\gamma_2\).
2. Encuentra las condiciones iniciales\[r(0)=r_0,\quad r'(0)=r_0',\quad \text{and} \quad \theta(0)=\theta_0,\quad \theta'(0)=\theta_0'\] requeridas para hacer del punto inicial el perigeo, y el movimiento a lo largo de la órbita en la dirección de aumentar\(\theta\). CONSEJO: Utilizar los resultados del Ejercicio 6.4.2

4. Un objeto con masa\(m\) se mueve en una órbita espiral\(r=c\theta^2\) bajo una fuerza central

\[{\bf F}(r,\theta)=f(r)(\cos\theta\,{\bf i}+\sin\theta\,{\bf j}).\]

Encuentra\(f\).

5. Un objeto con masa\(m\) se mueve en la órbita\(r=r_0e^{\gamma\theta}\) bajo una fuerza central

\[{\bf F}(r,\theta)=f(r)(\cos\theta\,{\bf i}+\sin\theta\,{\bf j}).\]

Encuentra\(f\).

6. Supongamos que un objeto con masa\(m\) se mueve bajo la fuerza central

\[{\bf F}(r,\theta)=-{mk\over r^3}(\cos\theta\,{\bf i}+\sin\theta\,{\bf j}),\]

con

\[r(0)=r_0,\quad r'(0)=r_0', \quad\text{and}\quad \theta(0)=\theta_0,\quad \theta'(0)=\theta_0',\]

donde\(h=r_0^2\theta_0'\ne0\).

1. Configurar un problema de valor inicial de segundo orden para\(u=1/r\) como una función de\(\theta\).
2. Determinar\(r=r(\theta)\) si (i)\(h^2<k\); (ii)\(h^2=k\); (iii)\(h^2>k\).