6.4: Movimiento bajo una fuerza central
- Page ID
- 115036
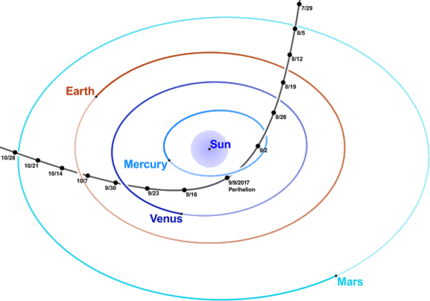
Ahora estudiaremos el movimiento de un objeto que se mueve bajo la influencia de una fuerza central; es decir, una fuerza cuya magnitud en cualquier punto\(P\) distinto del origen depende únicamente de la distancia desde\(P\) el origen, y cuya dirección a\(P\) es paralela a la línea conexión\(P\) y el origen, como se indica en la Figura 6.4.1 para el caso donde la dirección de la fuerza en cada punto es hacia el origen. Las fuerzas gravitacionales son fuerzas centrales; por ejemplo, como se menciona en la Sección 4.3, si asumimos que la Tierra es una esfera perfecta con densidad de masa constante entonces la ley de gravitación de Newton afirma que la fuerza ejercida sobre un objeto por el campo gravitacional de la Tierra es proporcional a la masa del objeto y inversamente proporcional al cuadrado de su distancia del centro de la Tierra, que tomamos como origen.
Si la posición inicial y los vectores de velocidad de un objeto que se mueve bajo una fuerza central son paralelos, entonces el movimiento posterior es a lo largo de la línea desde el origen hasta la posición inicial. Aquí asumiremos que los vectores de posición inicial y velocidad no son paralelos; en este caso el movimiento posterior está en el plano determinado por ellos. Por conveniencia tomamos esto para ser el\(xy\) -avión. Consideraremos el problema de determinar la curva atravesada por el objeto. Llamamos a esta curva la órbita.
Podemos representar una fuerza central en términos de coordenadas polares
\[x=r\cos\theta,\quad y=r\sin\theta \nonumber\]
como
\[{\bf F}(r,\theta)=f(r)(\cos\theta\,{\bf i}+\sin\theta\,{\bf j}). \nonumber\]
Suponemos que\(f\) es continuo para todos\(r>0\). La magnitud de\({\bf F}\) at\((x,y)=(r\cos\theta,r\sin\theta)\) es\(|f(r)|\), por lo que depende únicamente\(r\) de la distancia del punto al origen la dirección de\({\bf F}\) es del punto al origen si\(f(r)<0\), o del origen al punto si\(f(r)>0\). Mostraremos que la órbita de un objeto con masa\(m\) moviéndose bajo esta fuerza viene dada por
\[r(\theta)={1\over u(\theta)}, \nonumber\]

donde\(u\) está la solución de la ecuación diferencial
\[\label{eq:6.4.1} {d^2u\over d\theta^2}+u=-{1\over mh^2u^2}f(1/u),\]
y\(h\) es una constante definida a continuación.
La segunda ley de movimiento de Newton (\({\bf F}=m{\bf a}\)) dice que las coordenadas polares\(r=r(t)\) y\(\theta=\theta(t)\) de la partícula satisfacen la ecuación diferencial vectorial
\[\label{eq:6.4.2} m(r\cos\theta\,{\bf i}+r\sin\theta\,{\bf j})''= f(r)(\cos\theta\,{\bf i}+\sin\theta\,{\bf j}).\]
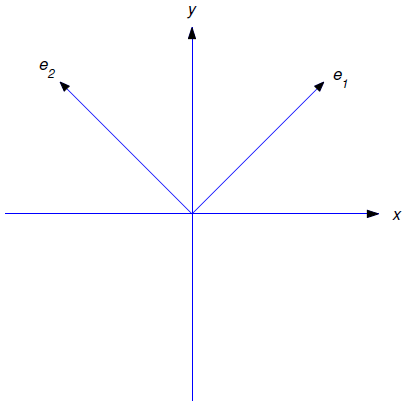
Para hacer frente a esta ecuación introducimos los vectores unitarios
\[{\bf e}_1=\cos\theta\,{\bf i}+\sin\theta\,{\bf j} \quad \text{and} \quad {\bf e}_2=-\sin\theta\,{\bf i}+\cos\theta\,{\bf j}. \nonumber\]
Obsérvese que\({\bf e}_1\) apunta en la dirección del incremento\(r\) y\({\bf e}_2\) apunta en la dirección del incremento\(\theta\) (Figura 6.4.2 ); además,
\[\label{eq:6.4.3} {d{\bf e}_1\over d\theta}={\bf e}_2,\quad {d{\bf e}_2\over d\theta}=-{\bf e}_1,\]
y
\[{\bf e}_1\cdot{\bf e}_2=\cos\theta(-\sin\theta)+\sin\theta\cos\theta=0, \nonumber\]
así\({\bf e}_1\) y\({\bf e}_2\) son perpendiculares. Recordando que el primo único\((')\) significa diferenciación con respecto a\(t\), vemos en la Ecuación\ ref {eq:6.4.3} y la regla de la cadena que
\[\label{eq:6.4.4} {\bf e}_1'=\theta'{\bf e}_2\quad \text{and} \quad {\bf e}_2'=-\theta'{\bf e}_1.\]
Ahora podemos escribir la Ecuación\ ref {eq:6.4.2} como
\[\label{eq:6.4.5} m(r{\bf e}_1)''=f(r){\bf e}_1.\]
Pero
\[(r{\bf e}_1)'=r'{\bf e}_1+r{\bf e}_1'=r'{\bf e}_1+r\theta'{\bf e}_2 \nonumber\]
(de la Ecuación\ ref {eq:6.4.4}), y
\[\begin{aligned} (r{\bf e}_1)''&=(r'{\bf e}_1+r\theta'{\bf e}_2)'\\ &=r''{\bf e}_1+r'{\bf e}_1'+(r\theta''+r'\theta'){\bf e}_2 +r\theta'{\bf e}_2'\\ &=r''{\bf e}_1+r'\theta'{\bf e}_2+(r\theta''+r'\theta'){\bf e}_2 -r(\theta')^2{\bf e}_1 \quad \mbox{from \eqref{eq:6.4.4}}\\ &=\left(r''-r(\theta')^2\right){\bf e}_1+(r\theta''+2r'\theta'){\bf e}_2.\end{aligned}\]
Sustituyendo esto en la ecuación\ ref {eq:6.4.5} rendimientos
\[m\left(r''-r(\theta')^2\right){\bf e}_1+m(r\theta''+2r'\theta'){\bf e}_2=f(r){\bf e}_1. \nonumber\]
Al igualar los coeficientes de\({\bf e}_1\) y\({\bf e}_2\) en los dos lados de esta ecuación vemos que
\[\label{eq:6.4.6} m\left(r''-r(\theta')^2\right)=f(r)\]
y
\[r\theta''+2r'\theta'=0. \nonumber\]
Multiplicar la última ecuación por\(r\) rendimientos
\[r^2\theta''+2rr'\theta'=(r^2\theta')'=0, \nonumber\]
por lo
\[\label{eq:6.4.7} r^2\theta'=h,\]
donde\(h\) es una constante que podemos escribir en términos de las condiciones iniciales como
\[h=r^2(0)\theta'(0). \nonumber\]
Dado que los vectores de posición y velocidad iniciales son
\[r(0){\bf e}_1(0)\quad \text{and} \quad r'(0){\bf e}_1(0)+r(0)\theta'(0){\bf e}_2(0), \nonumber\]
nuestra suposición de que estos dos vectores no son paralelos implica que\(\theta'(0)\ne0\), así\(h\ne0\).
Ahora vamos\(u=1/r\). Luego\(u^2=\theta'/h\) (de la Ecuación\ ref {eq:6.4.7}) y
\[r'=-{u'\over u^2}=-h\left(u'\over \theta'\right),\nonumber\]
lo que implica que
\[\label{eq:6.4.8} r'=-h{du\over d\theta},\]
desde
\[{u'\over\theta'}={du\over dt}\left/{d\theta\over dt}\right.= {du\over d\theta}.\nonumber\]
Ecuación diferenciadora\ ref {eq:6.4.8} con respecto a\(t\) rendimientos
\[r''=-h{d\over dt}\left({du\over d\theta}\right) =-h{d^2u\over d\theta^2}\theta',\nonumber\]
lo que implica que
\[r''=-h^2u^2{d^2u\over d\theta^2} \quad \text{since} \quad \theta'=hu^2.\nonumber\]
Sustituyendo de estas igualdades en la Ecuación\ ref {eq:6.4.6} y recordando que\(r=1/u\) rinde
\[-m\left(h^2u^2{d^2u\over d\theta^2}+{1\over u}h^2u^4\right) =f(1/u),\nonumber\]
y dividiendo por\(-mh^2u^2\) rendimientos Ecuación\ ref {eq:6.4.1}.
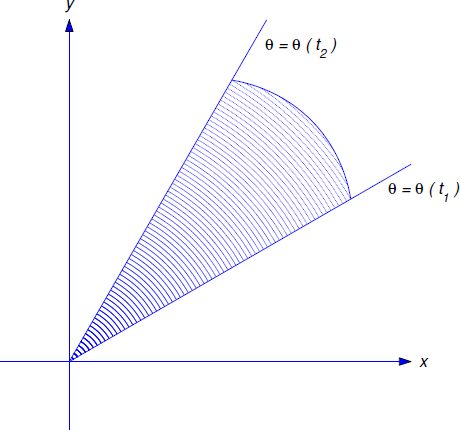
La ecuación\ ref {eq:6.4.7} tiene la siguiente interpretación geométrica, la cual se conoce como Segunda Ley de Kepler.
El vector de posición de un objeto que se mueve bajo una fuerza central barre áreas iguales en tiempos iguales;\(\) más precisamente\(,\) si\(\theta(t_1)\le\theta(t_2)\) entonces el área firmada del sector (Figura 6.4.3 ):
\[(x,y)=(r\cos\theta,r\sin\theta)\; :\; 0\le r\le r(\theta),\; \theta(t_1)\le\theta(t_2) \nonumber\]
está dado por
\[A={h(t_2-t_1)\over2},\nonumber\]
\(h=r^2\theta',\)donde hemos demostrado ser constantes.
- Prueba
-
Recordemos del cálculo que el área del sector sombreado en la Figura 6.4.3 es
\[A={1\over2}\int_{\theta(t_1)}^{\theta(t_2)} r^2(\theta)\,d\theta,\nonumber\]
donde\(r=r(\theta)\) está la representación polar de la órbita. Haciendo el cambio de\(\theta=\theta(t)\) rendimientos variables
\[\label{eq:6.4.9} A={1\over2}\int_{t_1}^{t_2} r^2(\theta(t))\theta'(t)\,dt.\]
Sin embargo, las ecuaciones\ ref {eq:6.4.7} y\ ref {eq:6.4.9} implican que
\[A={1\over2}\int_{t_1}^{t_2} h\,dt={h(t_2-t_1)\over2},\nonumber\]
que completa la prueba.
Movimiento bajo una fuerza de ley cuadrada inversa
En el caso especial donde\(f(r)=-mk/r^2=-mku^2\), así\({\bf F}\) puede interpretarse como una fuerza gravitacional, la Ecuación\ ref {eq:6.4.1} se convierte
\[\label{eq:6.4.10} {d^2u\over d\theta^2}+u={k\over h^2}.\]
La solución general de la ecuación complementaria
\[{d^2u\over d\theta^2}+u=0\nonumber\]
se puede escribir en forma de amplitud—fase como
\[u=A\cos(\theta-\phi),\nonumber\]
donde\(A\ge0\) y\(\phi\) es un ángulo de fase. Dado que\(u_p=k/h^2\) es una solución particular de la Ecuación\ ref {eq:6.4.10}, la solución general de la Ecuación\ ref {eq:6.4.10} es
\[u=A\cos(\theta-\phi)+{k\over h^2};\nonumber\]
por lo tanto, la órbita viene dada por
\[r=\left(A\cos(\theta-\phi)+{k\over h^2}\right)^{-1},\nonumber\]
que reescribimos como
\[\label{eq:6.4.11} r={\rho\over 1+e\cos(\theta-\phi)},\]
donde
\[\rho={h^2\over k}\quad \text{and} \quad e=A\rho.\nonumber\]
Una curva que satisface la Ecuación\ ref {eq:6.4.11} es una sección cónica con un enfoque en el origen (Ejercicio 6.4.1). La constante no negativa\(e\) es la excentricidad de la órbita, que es una elipse si\(e<1\) elipse (un círculo si\(e=0\)), una parábola si\(e=1\), o una hipérbola si\(e>1\).
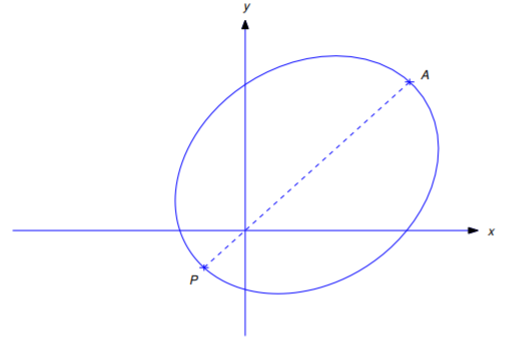
Si la órbita es una elipse, entonces los valores mínimo y máximo de\(r\) son
\[\begin{aligned} r_{\min}&={\rho\over1+e}\quad\mbox{(the perihelion distance is attained when $\theta=\phi$)} \\ r_{\max}&={\rho\over1-e}\quad \mbox{(the aphelion distance is attained when $\theta=\phi+\pi$)}.\end{aligned}\]
La figura 6.4.4 muestra una órbita elíptica típica. El punto\(P\) en la órbita donde\(r=r_{\min}\) está el perigeo y el punto\(A\) donde\(r=r_{\max}\) está el apogeo.
La órbita de la Tierra alrededor del Sol es aproximadamente una elipse con\(e\approx 0.017\),\(r_{\min}\approx 91 \times 10^6\) millas, y\(r_{\max}\approx 95\times 10^6\) millas. El cometa Halley tiene una órbita muy alargada aproximadamente elíptica alrededor del sol (Figura\(\PageIndex{5; left}\)), con\(e\approx 0.967\),\(r_{\min}\approx 55 \times10^6\) millas, y\(r_{\max}\approx 33 \times 10^8\) millas. Algunos cometas (el tipo no recurrente) tienen órbitas parabólicas o hiperbólicas como el objeto interestelar Oumuamua (Figura\(\PageIndex{5; right}\)).