9.3: Coeficientes indeterminados para ecuaciones de orden superior
- Page ID
- 114609
En esta sección consideramos la ecuación de coeficiente constante
\[\label{eq:9.3.1} a_0y^{(n)}+a_1y^{(n-1)}+\cdots+a_ny=F(x),\]
donde\(n\ge3\) y\(F\) es una combinación lineal de funciones de la forma
\[e^{\alpha x}\left(p_0+p_1x+\cdots+p_kx^k\right) \nonumber\]
o
\[e^{\lambda x}\left[\left(p_0+p_1x+\cdots+p_kx^k\right) \cos\omega x+ \left(q_0+q_1x+\cdots+q_kx^k\right) \sin\omega x\right].\nonumber\]
Del Teorema 9.1.5, la solución general de la Ecuación\ ref {eq:9.3.1} es\(y=y_p+y_c\), donde\(y_p\) está una solución particular de la Ecuación\ ref {eq:9.3.1} y\(y_c\) es la solución general de la ecuación complementaria
\[a_0y^{(n)}+a_1y^{(n-1)}+\cdots+a_ny=0.\nonumber\]
En la Sección 9.2 aprendimos a encontrar\(y_c\). Aquí aprenderemos a encontrar\(y_p\) cuándo la función de forzamiento tiene la forma señalada anteriormente. El procedimiento que utilizamos es una generalización del método que utilizamos en las Secciones 5.4 y 5.5, y de nuevo se llama método de coeficientes indeterminados. Dado que las ideas subyacentes son las mismas que las de esta sección, daremos una presentación informal basada en ejemplos.
Forzar las funciones de la forma\(e^{αx}(p_0 + p_1x + ... + p_kx^k)\)
Primero consideramos ecuaciones de la forma
\[a_0y^{(n)}+a_1y^{(n-1)}+\cdots+a_ny=e^{\alpha x}\left(p_0+p_1x+\cdots+p_kx^k\right).\nonumber\]
Encuentre una solución particular de
\[\label{eq:9.3.2} y'''+3y''+2y'-y=e^x(21+24x+28x^2+5x^3).\]
Solución
Sustituyendo
\[\begin{align*} y&=ue^x,\\ y'&=e^x(u'+u),\\ y''&=e^x(u''+2u'+u),\\ y'''&=e^x(u'''+3u''+3u'+u)\end{align*}\]
en Ecuación\ ref {eq:9.3.2} y cancelando\(e^x\) rendimientos
\[(u'''+3u''+3u'+u)+3(u''+2u'+u)+2(u'+u)-u =21+24x+28x^2+5x^3, \nonumber\]
o
\[\label{eq:9.3.3} u'''+6u''+11u'+5u=21+24x+28x^2+5x^3.\]
Como lo desconocido\(u\) aparece a la izquierda, podemos ver que la Ecuación\ ref {eq:9.3.3} tiene una solución particular de la forma
\[u_p=A+Bx+Cx^2+Dx^3. \nonumber\]
Entonces
\[\begin{aligned} u_p'&=B+2Cx+3Dx^2\\ u_p''&=2C+6Dx\\ u_p'''&=6D.\end{aligned}\]
Sustituyendo de las últimas cuatro ecuaciones en el lado izquierdo de la ecuación\ ref {eq:9.3.3} rendimientos
\[\begin{aligned} u_p'''+6u_p''+11u_p'+5u_p&=6D+6(2C+6Dx)+11(B+2Cx+3Dx^2)\\ &\:\:+5(A+Bx+Cx^2+Dx^3)\\ &=(5A+11B+12C+6D)+(5B+22C+36D)x\\&\:\:+(5C+33D)x^2+5Dx^3.\end{aligned}\]
La comparación de coeficientes de potencias similares de\(x\) en los lados derechos de esta ecuación y la Ecuación\ ref {eq:9.3.3} muestra que\(u_p\) satisface la Ecuación\ ref {eq:9.3.3} si
\[\begin{array}{rcr} 5D&=5\phantom{.}\\ 5C+33D&=28\phantom{.}\\ 5B+22C+36D&=24\phantom{.}\\ 5A+11B+12C+\phantom{3}6D&=21. \end{array}\nonumber \]
Resolver estas ecuaciones sucesivamente rinde\(D=1\),\(C=-1\),\(B=2\),\(A=1\). Por lo tanto
\[u_p=1+2x - x^2 + x^3 \nonumber\]
es una solución particular de la Ecuación\ ref {eq:9.3.3}, entonces
\[y_p = e^xu_p = e^x(1+2x-x^2+x^3) \nonumber\]
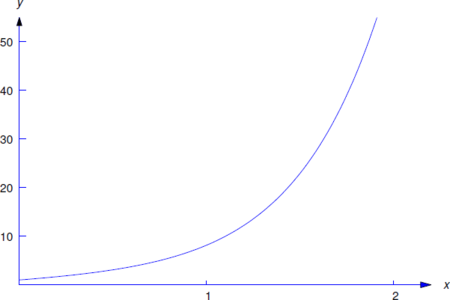
es una solución particular de la Ecuación\ ref {eq:9.3.2} (Figura 9.3.1 ).
Encuentre una solución particular de
\[\label{eq:9.3.4} y^{(4)}-y'''-6y''+4y'+8y=e^{2x}(4+19x+6x^2).\]
Solución
Sustituyendo
\[\begin{aligned} y&=ue^{2x},\\ y'&=e^{2x}(u'+2u),\\ y''&=e^{2x}(u''+4u'+4u),\\ y'''&=e^{2x}(u'''+6u''+12u'+8u),\\ y^{(4)}&=e^{2x}(u^{(4)}+8u'''+24u''+32u'+16u)\end{aligned}\]
en Ecuación\ ref {eq:9.3.4} y cancelar\(e^{2x}\) rendimientos
\[\begin{aligned} &&(u^{(4)}+8u'''+24u''+32u'+16u)-(u'''+6u''+12u'+8u)\\ &&-6(u''+4u'+4u)+4(u'+2u)+8u=4+19x+6x^2,\end{aligned}\]
o
\[\label{eq:9.3.5} u^{(4)}+7u'''+12u''=4+19x+6x^2.\]
Ya que\(u\) ni\(u'\) aparecen a la izquierda, podemos ver que la Ecuación\ ref {eq:9.3.5} tiene una solución particular de la forma
\[\label{eq:9.3.6} u_p=Ax^2+Bx^3+Cx^4.\]
Entonces
\[\begin{aligned} u_p'&=2Ax+3Bx^2+4Cx^3\\ u_p''&=2A+6Bx+12Cx^2\\ u_p'''&=6B+24Cx\\ u_p^{(4)}&=24C.\end{aligned}\]
Sustituyendo\(u_p''\),\(u_p'''\), y\(u_p^{(4)}\) en el lado izquierdo de la ecuación\ ref {eq:9.3.5} rendimientos
\[\begin{aligned} u_p^{(4)}+7u_p'''+12u_p''&=24C+7(6B+24Cx)+12(2A+6Bx+12Cx^2)\\ &=(24A+42B+24C)+(72B+168C)x+144Cx^2.\end{aligned}\]
La comparación de coeficientes de potencias similares de\(x\) en los lados derechos de esta ecuación y la Ecuación\ ref {eq:9.3.5} muestra que\(u_p\) satisface la Ecuación\ ref {eq:9.3.5} si
\[\begin{array}{rrr} 144C&=6\phantom{.}\\ 72B+168C&=19\phantom{.}\\ 24A+42B+\phantom{1}24C&=4. \end{array}\nonumber \]
Resolver estas ecuaciones sucesivamente rinde\(C=1/24\),\(B=1/6\),\(A=-1/6\). Al sustituirlas en la ecuación\ ref {eq:9.3.6} se muestra que
\[u_p=\dfrac{x^2}{24}(-4+4x+x^2) \nonumber\]
es una solución particular de la Ecuación\ ref {eq:9.3.5}, entonces
\[y_p=e^{2x}u_p={x^2e^{2x}\over24}(-4+4x+x^2) \nonumber\]
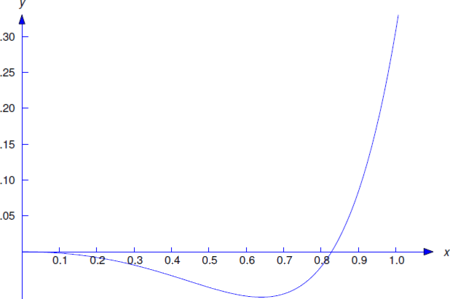
es una solución particular de la Ecuación\ ref {eq:9.3.4} (Figura 9.3.2 ).
Forzar las funciones de la forma\(e^{αx}(P(x) \cos ωx + Q(x) \sin ωx)\)
Consideramos ahora ecuaciones de la forma
\[a_0y^{(n)}+a_1y^{(n-1)}+\cdots+a_ny= e^{\lambda x}\left(P(x)\cos\omega x+Q(x)\sin\omega x\right), \nonumber\]
donde\(P\) y\(Q\) son polinomios.
Encuentre una solución particular de
\[\label{eq:9.3.7} y'''+y''-4y'-4y=e^x[(5-5x)\cos x+(2+5x)\sin x].\]
Solución
Sustituyendo
\[\begin{aligned} y&=ue^x,\\ y'&=e^x(u'+u),\\ y''&=e^x(u''+2u'+u),\\ y'''&=e^x(u'''+3u''+3u'+u)\end{aligned}\]
en Ecuación\ ref {eq:9.3.7} y cancelando\(e^x\) rendimientos
\[(u'''+3u''+3u'+u)+(u''+2u'+u)-4(u'+u)-4u =(5-5x)\cos x+(2+5x)\sin x,\nonumber\]
o
\[\label{eq:9.3.8} u'''+4u''+u'-6u=(5-5x)\cos x+(2+5x)\sin x.\]
Dado que\(\cos x\) y no\(\sin x\) son soluciones de la ecuación complementaria
\[u'''+4u''+u'-6u=0,\nonumber\]
un teorema análogo al Teorema 5.5.1 implica que la Ecuación\ ref {eq:9.3.8} tiene una solución particular de la forma
\[\label{eq:9.3.9} u_p=(A_0+A_1x)\cos x+(B_0+B_1x)\sin x.\]
Entonces
\[\begin{aligned} u_p'=(A_1+B_0+B_1x)\cos x+(B_1-A_0-A_1x)\sin x,\\ u_p''=(2B_1-A_0-A_1x)\cos x-(2A_1+B_0+B_1x)\sin x,\\ u_p'''=-(3A_1+B_0+B_1x)\cos x-(3B_1-A_0-A_1x)\sin x,\\\end{aligned}\nonumber \]
por lo
\[ u_p'''+4u_p''+u_p'-6u_p =-\left[10A_0+2A_1-8B_1+10A_1x\right]\cos x - \left[10B_0+2B_1+8A_1+10B_1x\right]\sin x. \nonumber\]
Comparando los coeficientes de\(x\cos x\),\(x\sin x\),\(\cos x\), y\(\sin x\) aquí con los coeficientes correspondientes en la Ecuación\ ref {eq:9.3.8} muestra que\(u_p\) es una solución de la Ecuación\ ref {eq:9.3.8} si
\[\begin{array}{rrr} -10A_1&=-5\phantom{.}\\ -10B_1&=\phantom{-}5\phantom{.}\\ -10A_0-2A_1+8B_1&=5\phantom{.}\\ -10B_0-2B_1-8A_1&=2. \end{array}\nonumber \]
Resolver las dos primeras ecuaciones rinde\(A_1=1/2\),\(B_1=-1/2\). Sustituyendo estos en las dos últimas ecuaciones rinde
\[\begin{aligned} -10A_0&=5+2A_1-8B_1=10\phantom{.}\\ -10B_0&=2+2B_1+8A_1=5, \end{aligned}\]
entonces\(A_0=-1\),\(B_0=-1/2\). Sustituir\(A_0=-1\),\(A_1=1/2\),\(B_0=-1/2\),\(B_1=-1/2\) en la Ecuación\ ref {eq:9.3.9} muestra que
\[u_p=-\frac{1}{2}\left[(2-x)\cos x+(1+x)\sin x\right] \nonumber\]
es una solución particular de la Ecuación\ ref {eq:9.3.8}, entonces
\[y_p=e^xu_p=-{e^x\over2}\left[(2-x)\cos x+(1+x)\sin x\right] \nonumber\]
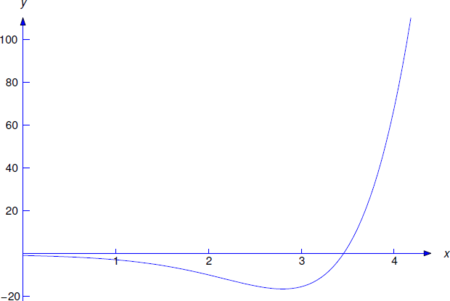
es una solución particular de la Ecuación\ ref {eq:9.3.7} (Figura 9.3.3 ).
Encuentre una solución particular de
\[\label{eq:9.3.10} y'''+4y''+6y'+4y= e^{-x}\left[(1-6x)\cos x-(3+2x)\sin x\right].\]
Solución
Sustituyendo
\[\begin{aligned} y&=ue^{-x},\\ y'&=e^{-x}(u'-u),\\ y''&=e^{-x}(u''-2u'+u),\\ y'''&=e^{-x}(u'''-3u''+3u'-u)\end{aligned}\]
en Ecuación\ ref {eq:9.3.10} y cancelando\(e^{-x}\) rendimientos
\[(u'''-3u''+3u'-u)+4(u''-2u'+u)+6(u'-u)+4u =(1-6x)\cos x-(3+2x)\sin x, \nonumber\]
o
\[\label{eq:9.3.11} u'''+u''+u'+u=(1-6x)\cos x-(3+2x)\sin x.\]
Dado que\(\cos x\) y\(\sin x\) son soluciones de la ecuación complementaria
\[u'''+u''+u'+u=0, \nonumber\]
un teorema análogo al Teorema 5.5.1 implica que la Ecuación\ ref {eq:9.3.11} tiene una solución particular de la forma
\[\label{eq:9.3.12} u_p=(A_0x+A_1x^2)\cos x+(B_0x+B_1x^2)\sin x.\]
Entonces
\[\begin{align*} u_p' =&[A_0+(2A_1+B_0)x+B_1x^2]\cos x+[B_0+(2B_1-A_0)x-A_1x^2]\sin x,\\ u_p'' =&[2A_1+2B_0-(A_0-4B_1)x-A_1x^2]\cos x\\&+ [2B_1-2A_0-(B_0+4A_1)x-B_1x^2]\sin x,\\ u_p''' =& -[3A_0-6B_1+(6A_1+B_0)x+B_1x^2]\cos x \\&-[3B_0+6A_1+(6B_1-A_0)x-A_1x^2]\sin x,\end{align*}\]
por lo
\[\begin{align*} u_p'''+u_p''+u_p'+u_p =& -[2A_0-2B_0-2A_1-6B_1+(4A_1-4B_1)x]\cos x\\ &-[2B_0+2A_0-2B_1+6A_1+(4B_1+4A_1)x]\sin x. \end{align*}\]
Comparando los coeficientes de\(x\cos x\),\(x\sin x\),\(\cos x\), y\(\sin x\) aquí con los coeficientes correspondientes en la Ecuación\ ref {eq:9.3.11} muestra que\(u_p\) es una solución de la Ecuación\ ref {eq:9.3.11} si
\[\begin{array}{rcr} -4A_1+4B_1&=-6\phantom{.}\\ -4A_1-4B_1&=-2\phantom{.}\\ -2A_0+2B_0+2A_1+6B_1&=\phantom{-}1\phantom{.}\\ -2A_0-2B_0-6A_1+2B_1&=-3. \end{array}\nonumber \]
Resolver las dos primeras ecuaciones rinde\(A_1=1\),\(B_1=-1/2\). Sustituyendo estos en las dos últimas ecuaciones rinde
\[\begin{aligned} -2A_0+2B_0&=\phantom{-}1-2A_1-6B_1=2\phantom{.}\\ -2A_0-2B_0&=-3+6A_1-2B_1=4, \end{aligned}\]
así\(A_0=-3/2\) y\(B_0=-1/2\). Sustituir\(A_0=-3/2\),\(A_1=1\),\(B_0=-1/2\),\(B_1=-1/2\) en la Ecuación\ ref {eq:9.3.12} muestra que
\[u_p=- \dfrac{x}{2}\left[(3-2x)\cos x+(1+x)\sin x\right] \nonumber\]
es una solución particular de la Ecuación\ ref {eq:9.3.11}, entonces
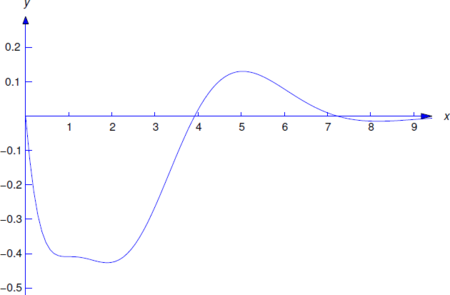
\[y_p=e^{-x}u_p=-{xe^{-x}\over2}\left[(3-2x)\cos x+(1+x)\sin x\right] \nonumber\]
(Figura 9.3.4 ) es una solución particular de la Ecuación\ ref {eq:9.3.10}.


