12.1: La Ecuación del Calor
- Page ID
- 114788
Comenzamos el estudio de ecuaciones diferenciales parciales con el problema del flujo de calor en una barra uniforme de longitud\(L\), situada en el\(x\) eje con un extremo en el origen y el otro en\(x = L\) (Figura 12.1.1 ).
Suponemos que la barra está perfectamente aislada excepto posiblemente en sus puntos finales, y que la temperatura es constante en cada sección transversal y por lo tanto depende únicamente de\(x\) y\(t\). También asumimos que las propiedades térmicas de la barra son independientes de\(x\) y\(t\). En este caso, se puede demostrar que la temperatura\(u = u(x, t)\) en el tiempo\(t\) en un punto\(x\) unidades del origen satisface la ecuación diferencial parcial
\[u_{t}=a^{2}u_{xx},\quad 0<x<L,\quad t>0,\nonumber\]
donde\(a\) es una constante positiva determinada por las propiedades térmicas. Esta es la ecuación del calor.
Para determinar\(u\), debemos especificar la temperatura en cada punto de la barra cuando\(t=0\), digamos
\[u(x,0)=f(x),\quad 0\le x\le L. \nonumber \]
A esto lo llamamos la condición inicial. También debemos especificar condiciones de contorno que\(u\) deben cumplir en los extremos de la barra para todos\(t>0\). Llamaremos a este problema un problema de valor de límite inicial.
Comenzamos con las condiciones de contorno\(u(0,t)=u(L,t)=0\), y escribimos el problema del valor de límite inicial como
\[\label{eq:12.1.1} \begin{array}{c}{u_{t}=a^{2}u_{xx},\quad 0<x<L,\quad t>0,}\\{u(0,t)=0,\quad u(L,t)=0,\quad t>0,}\\{u(x,0)=f(x),\quad 0\leq x\leq L.}\end{array}\]
Nuestro método para resolver este problema se llama separación de variables (no debe confundirse con el método de separación de variables utilizado en la Sección 2.2 para resolver ecuaciones diferenciales ordinarias). Comenzamos por buscar funciones del formulario
\[v(x,t)=X(x)T(t) \nonumber \]
que no son idénticamente cero y satisfacen
\[v_t=a^2v_{xx},\quad v(0,t)=0,\quad v(L,t)=0 \nonumber \]
para todos\((x,t)\). Desde
\[v_t=XT' \quad \text{and} \quad v_{xx}=X''T, \nonumber \]
\(v_t=a^2v_{xx}\)si y solo si
\[XT'=a^2X''T, \nonumber \]
que reescribimos como
\[{T'\over a^2T}={X''\over X}. \nonumber \]
Dado que la expresión de la izquierda es independiente de\(x\) mientras que la de la derecha es independiente de\(t\), esta ecuación puede sostenerse para todos\((x,t)\) solo si los dos lados son iguales a la misma constante, a la que llamamos constante de separación, y la escribimos como\(-\lambda\); así,
\[{X''\over X}={T'\over a^2T}=-\lambda. \nonumber \]
Esto es equivalente a
\[X''+\lambda X=0 \nonumber \]
y
\[\label{eq:12.1.2} T'=-a^2\lambda T.\]
Desde\(v(0,t)=X(0)T(t)=0\)\(v(L,t)=X(L)T(t)=0\) y y no queremos\(T\) ser idénticamente cero,\(X(0)=0\) y\(X(L)=0\). Por lo tanto,\(\lambda\) debe ser un valor propio del problema del valor límite
\[\label{eq:12.1.3} X''+\lambda X=0,\quad X(0)=0,\quad X(L)=0,\]
y\(X\) debe ser una\(\lambda\) -función propia. Del Teorema 11.1.2, los valores propios de la Ecuación\ ref {eq:12.1.3} son\(\lambda_n=n^2\pi^2/L^2\), con funciones propias asociadas
\[X_n=\sin{n\pi x\over L}, \quad n=1,2,3,\dots. \nonumber \]
Sustituyendo\(\lambda=n^2\pi^2/L^2\) en la ecuación\ ref {eq:12.1.2} rendimientos
\[T'=-(n^2\pi^2a^2/L^2)T, \nonumber \]
que tiene la solución
\[T_n=e^{-n^2\pi^2a^2t/L^2}. \nonumber \]
Ahora vamos
\[v_n(x,t)=X_n(x)T_n(t)=e^{-n^2\pi^2a^2t/L^2}\sin{n\pi x\over L},\quad n=1,2,3,\dots \nonumber \]
Desde
\[v_n(x,0)=\sin{n\pi x\over L}, \nonumber \]
\(v_n\)satisface la Ecuación\ ref {eq:12.1.1} con\(f(x)=\sin n\pi x/L\). De manera más general, si\(\alpha_1,\dots,\alpha_m\) son constantes y
\[u_m(x,t)= \sum_{n=1}^m \alpha_ne^{-n^2\pi^2a^2t/L^2}\sin{n\pi x\over L}, \nonumber \]
entonces\(u_m\) satisface la Ecuación\ ref {eq:12.1.1} con
\[f(x)=\sum_{n=1}^m \alpha_n\sin{n\pi x\over L}. \nonumber \]
Esto motiva la siguiente definición.
La solución formal del problema del valor de límite inicial
\[\label{eq:12.1.4} \begin{array}{c}{u_{t}=a^{2}u_{xx},\quad 0<x<L,\quad t>0,}\\{u(0,t)=0,\quad u(L,t)=0,\quad t>0,}\\{u(x,0)=f(x),\quad 0\leq x\leq L}\end{array}\]
es
\[\label{eq:12.1.5} u(x,t)=\sum_{n=1}^\infty \alpha_ne^{-n^2\pi^2a^2t/L^2}\sin{n\pi x\over L},\]
donde
\[S(x)=\sum_{n=1}^\infty \alpha_n\sin{n\pi x\over L} \nonumber \]
es la serie sinusoidal de Fourier de\(f\) on\([0,L]\); es decir,
\[\alpha_n= \dfrac{2}{L} \int_0^L f(x) \sin \dfrac{n\pi x}{L} \,dx. \nonumber \]
Usamos el término “solución formal” en esta definición porque no es en general cierto que la serie infinita en la Ecuación\ ref {eq:12.1.5} realmente satisfaga todos los requisitos del problema del valor de límite inicial Ecuación\ ref {eq:12.1.4} cuando lo hace, decimos que es una solución real de la Ecuación\ ref {eq:12.1.4}.
Debido a los exponenciales negativos en la Ecuación\ ref {eq:12.1.5},\(u\) converge para todos\((x,t)\) con\(t>0\) (Ejercicio 12.1.54). Dado que cada término en la Ecuación\ ref {eq:12.1.5} satisface la ecuación de calor y las condiciones límite en la Ecuación\ ref {eq:12.1.4},\(u\) también tiene estas propiedades si\(u_t\) y se\(u_{xx}\) pueden obtener diferenciando la serie en la Ecuación\ ref {eq:12.1.5} término por término una vez con respecto a \(t\)y dos veces con respecto a\(x\), para\(t>0\). Sin embargo, no siempre es legítimo diferenciar una serie infinita término por término. El siguiente teorema da una condición suficiente útil para la legitimidad de término por término diferenciación de una serie infinita. Omitimos la prueba.
Una serie infinita convergente
\[W(z)=\sum_{n=1}^\infty w_n(z) \nonumber\]
se puede diferenciar término por término en un intervalo cerrado\([z_1,z_2]\) para obtener
\[W'(z)=\sum_{n=1}^\infty w_n'(z) \nonumber\]
\((\)donde los derivados en\(z=z_1\) y\(z=z_2\) son unilaterales\()\) siempre que\(w_n'\) sea continuo en\([z_1,z_2]\) y
\[|w_n'(z)|\le M_n,\quad z_1\le z\le z_2,\quad n=1,2,3,\dots, \nonumber\]
donde\(M_1,\)\(M_2,\)...,\(M_n,\)..., son constantes tales que la serie\(\sum_{n=1}^\infty M_n\) converge.
El teorema 12.1.2 , aplicado dos veces con\(z=x\) y una vez con\(z=t\), demuestra que\(u_{xx}\) y se\(u_t\) puede obtener diferenciando\(u\) término por término si\(t>0\) (Ejercicio 12.1.54). Por lo tanto,\(u\) satisface la ecuación de calor y las condiciones de límite en la Ecuación\ ref {eq:12.1.4} para\(t>0\). Por lo tanto, ya que\(u(x,0)=S(x)\) for\(0\le x\le L\),\(u\) es una solución real de la Ecuación\ ref {eq:12.1.4} si y sólo si\(S(x)=f(x)\) para\(0\le x\le L\). Del Teorema 11.3.2, esto es cierto si\(f\) es continuo y poco a poco suave\([0,L]\), y\(f(0)=f(L)=0\).
En este capítulo vamos a definir soluciones formales de varios tipos de problemas. Cuando le pedimos que resuelva este tipo de problemas, siempre queremos decir que debe encontrar una solución formal.
Resolver Ecuación\ ref {eq:12.1.4} con\(f(x)=x(x^2-3Lx+2L^2)\).
Solución
Del Ejemplo [ejemplo:11.3.6}, la serie sinusoidal de Fourier de\(f\) on\([0,L]\) es
\[S(x)=\frac{12L^{3}}{\pi ^{3}}\sum_{n=1}^{\infty}\frac{1}{n^{3}}\sin \frac{n\pi x}{L}\nonumber\]
Por lo tanto
\[u(x,t)=\frac{12L^{3}}{\pi ^{3}}\sum_{n=1}^{\infty }\frac{1}{n^{3}} e^{-n^{2}\pi ^{2}a^{2}t/L^{2}}\sin\frac{n\pi x}{L}\nonumber \]
Si ambos extremos de la barra están aislados para que no pueda pasar calor a través de ellos, entonces las condiciones límite son
\[u_x(0,t)=0,\quad u_x(L,t)=0,\quad t>0. \nonumber\]
Te dejamos a ti (Ejercicio 12.1.1) usar el método de separación de variables y Teorema 11.1.3 para motivar la siguiente definición.
La solución formal del problema del valor de límite inicial
\[\label{eq:12.1.6} \begin{array}{c}{u_{t}=a^{2}u_{xx},\quad 0<x<L,\quad t>0,}\\{u_{x}(0,t)=0,\quad u_{x}(L,t)=0,\quad t>0,}\\{u(x,0)=f(x),\quad 0\leq x\leq L}\end{array}\]
es
\[u(x,t)=\alpha_0+\sum_{n=1}^\infty \alpha_ne^{-n^2\pi^2 a^2t/L^2}\cos{n\pi x\over L}, \nonumber\]
donde
\[C(x)=\alpha_0+\sum_{n=1}^\infty \alpha_n\cos{n\pi x\over L} \nonumber\]
es la serie coseno de Fourier de\(f\) on es\([0,L];\) decir,
\[\alpha_0={1\over L}\int_0^Lf(x)\,dx \quad \text{and} \quad \alpha_n={2\over L}\int_0^Lf(x)\cos{n\pi x\over L}\,dx,\quad n=1,2,3,\dots. \nonumber\]
Resolver Ecuación\ ref {eq:12.1.6} con\(f(x)=x\).
Solución
Del Ejemplo 11.3.1, la serie coseno de Fourier de\(f\) on\([0,L]\) es
\[C(x)=\frac{L}{2}-\frac{4L}{\pi ^{2}}\sum_{n=1}^{\infty}\frac{1}{(2n-1)^{2}}\cos \frac{(2n-1)\pi x}{L}\nonumber \]
Por lo tanto
\[u(x,t)={L\over2}-{4L\over\pi^2}\sum_{n=1}^\infty {1\over(2n-1)^2} e^{-(2n-1)^2\pi^2a^2t/L^2}\cos{(2n-1)\pi x\over L}. \nonumber\]
Te dejamos a ti (Ejercicio 12.1.2) utilizar el método de separación de variables y Teorema 11.1.4 para motivar la siguiente definición.
La solución formal del problema del valor de límite inicial
\[\label{eq:12.1.7} \begin{array}{c}{u_{t}=a^{2}u_{xx},\quad 0<x<L,\quad t>0,}\\{u(0,t)=0,\quad u_{x}(L,t)=0,\quad t>0,}\\{u(x,0)=f(x),\quad 0\leq x\leq L}\end{array}\]
es
\[u(x,t)=\sum_{n=1}^\infty \alpha_ne^{-(2n-1)^2\pi^2a^2t/4L^2}\sin{(2n-1)\pi x\over2L},\nonumber\]
donde
\[S_M(x)=\sum_{n=1}^\infty \alpha_n\sin{(2n-1)\pi x\over2L}\nonumber\]
es la serie sinusoidal mixta de Fourier de\(f\) on es\([0,L];\) decir,
\[\alpha_n={2\over L}\int_0^Lf(x)\sin{(2n-1)\pi x\over2L}\,dx.\nonumber\]
Resolver Ecuación\ ref {eq:12.1.7} con\(f(x)=x\).
Solución
Del Ejemplo 11.3.4, la serie de seno mixto de Fourier de\(f\) on\([0,L]\) es
\[S_M(x)=-{8L\over\pi^2}\sum_{n=1}^\infty{(-1)^n\over(2n-1)^2} \sin{(2n-1)\pi x\over2L}. \nonumber\]
Por lo tanto
\[u(x,t)=-{8L\over\pi^2}\sum_{n=1}^\infty{(-1)^n\over(2n-1)^2} e^{-(2n-1)^2\pi^2a^2t/4L^2}\sin{(2n-1)\pi x\over2L}. \nonumber\]
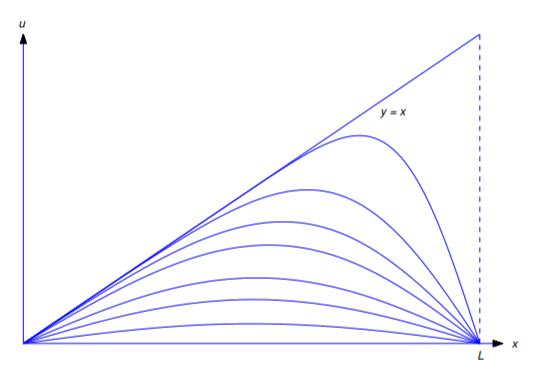
La figura 12.1.2 muestra un gráfico de\(u=u(x,t)\) trazado con respecto a\(x\) para diversos valores de\(t\). La línea\(y=x\) corresponde a\(t=0\). Las otras curvas corresponden a valores positivos de\(t\). A medida que\(t\) aumenta, las gráficas se acercan a la línea\(u=0\).
Te dejamos a ti (Ejercicio 12.1.3) utilizar el método de separación de variables y Teorema 11.1.5 para motivar la siguiente definición.
La solución formal del problema del valor de límite inicial
\[\label{eq:12.1.8} \begin{array}{c}{u_{t}=a^{2}u_{xx},\quad 0<x<L,\quad t>0,}\\{u_{x}(0,t)=0,\quad u(L,t)=0,\quad t>0,}\\{u(x,0)=f(x),\quad 0\leq x\leq L}\end{array}\]
es
\[u(x,t)=\sum_{n=1}^\infty \alpha_ne^{-(2n-1)^2\pi^2a^2t/4L^2}\cos{(2n-1)\pi x\over2L},\nonumber\]
donde
\[C_M(x)=\sum_{n=1}^\infty \alpha_n\cos{(2n-1)\pi x\over2L}\nonumber\]
es la serie mixta de coseno de Fourier de\(f\) on\([0,L]\); es decir,
\[\alpha_n={2\over L}\int_0^Lf(x)\cos{(2n-1)\pi x\over2L}\,dx.\nonumber\]
Resolver Ecuación\ ref {eq:12.1.8} con\(f(x)=x-L\).
Solución
Del Ejemplo 11.3.3, la serie mixta de coseno de Fourier de\(f\) on\([0,L]\) es
\[C_M(x)=-{8L\over\pi^2}\sum_{n=1}^\infty{1\over(2n-1)^2} \cos{(2n-1)\pi x\over2L}.\nonumber\]
Por lo tanto
\[u(x,t)=-{8L\over\pi^2}\sum_{n=1}^\infty{1\over(2n-1)^2} e^{-(2n-1)^2\pi^2a^2t/4L^2}\cos{(2n-1)\pi x\over2L}.\nonumber\]
Problemas no homogéneos
Un problema de la forma
\[\label{eq:12.1.9} \begin{array}{c}{u_{t}=a^{2}u_{xx}+h(x),\quad 0<x<L,\quad t>0,}\\{u(0,t)=u_{0},\quad u(L,t)=u_{L},\quad t>0,}\\{u(x,0)=f(x),\quad 0\leq x\leq L}\end{array}\]
puede transformarse en un problema que puede resolverse mediante la separación de variables. Escribimos
\[\label{eq:12.1.10} u(x,t)=v(x,t)+q(x),\]
donde\(q\) se va a determinar. Entonces
\[u_t=v_t \quad \text{and} \quad u_{xx}=v_{xx}+q''\nonumber\]
así\(u\) satisface la Ecuación\ ref {eq:12.1.9} si\(v\) satisface
\[\begin{array}{c}{v_{t}=a^{2}v_{xx}+a^{2}q''(x)+h(x),\quad 0<x<L,\quad t>0,}\\{v(0,t)=u_{0}-q(0),\quad v(L,t)=u_{L}-q(L),\quad t>0,}\\{v(x,0)=f(x)-q(x),\quad 0\leq x\leq L.}\end{array}\nonumber \]
Esto reduce a
\[\label{eq:12.1.11} \begin{array}{c}{v_{t}=a^{2}v_{xx},\quad 0<x<L,\quad t>0,}\\{v(0,t)=0,\quad v(L,t)=0,\quad t>0,}\\{v(x,0)=f(x)-q(x),\quad 0\leq x\leq L}\end{array}\]
si
\[a^2q''+h(x)=0,\quad q(0)=u_0,\quad q(L)=u_L.\nonumber\]
Podemos obtener\(q\) integrando\(q''=-h/a^2\) dos veces y eligiendo las constantes de integración para que\(q(0)=u_0\) y\(q(L)=u_L\). Entonces podemos resolver la Ecuación\ ref {eq:12.1.11} para\(v\) por separación de variables, y la Ecuación\ ref {eq:12.1.10} es la solución de la Ecuación\ ref {eq:12.1.9}.
Resolver
\[\begin{array}{c}{u_{t}=u_{xx}-2,\quad 0<x<1,\quad t>0,}\\{u(0,t)=-1,\quad u(1,t)=1,\quad t>0,}\\{u(x,0)=x^{3}-2x^{2}+3x-1,\quad 0\leq x\leq 1.}\end{array}\nonumber \]
Solución
Te dejamos a ti demostrar que
\[q(x)=x^2+x-1\nonumber\]
satisface
\[q''-2=0,\quad q(0)=-1,\quad q(1)=1.\nonumber\]
Por lo tanto
\[u(x,t)=v(x,t)+x^2+x-1,\nonumber\]
donde
\[v_{t}=v_{xx},\quad 0<x<1,\quad t>0,\nonumber \]
\[v(0,t)=0,\quad v(1,t)=0,\quad t>0,\nonumber\]
y
\[v(x,0)=x^3-2x^2+3x-1-x^2-x+1=x(x^2-3x+2).\nonumber\]
Del Ejemplo 12.1.1 con\(a=1\) y\(L=1\),
\[v(x,t)= {12\over\pi^3}\sum_{n=1}^\infty{1\over n^3} e^{-n^2\pi^2t}\sin n\pi x.\nonumber\]
Por lo tanto
\[u(x,t)=x^2+x-1+ {12\over\pi^3}\sum_{n=1}^\infty{1\over n^3} e^{-n^2\pi^2t}\sin n\pi x. \nonumber\]
Un procedimiento similar funciona si las condiciones de contorno en la Ecuación\ ref {eq:12.1.11} se reemplazan por condiciones de límite mixtas
\[u_x(0,t)=u_0,\quad u(L,t)=u_L,\quad t>0\nonumber\]
o
\[u(0,t)=u_0,\quad u_x(L,t)=u_L,\quad t>0;\nonumber\]
sin embargo, esto no es cierto en general para las condiciones de límite
\[u_x(0,t)=u_0,\quad u_x(L,t)=u_L,\quad t>0.\nonumber\]
(Ver Ejercicio 12.1.47.)
Uso de la tecnología
Los experimentos numéricos pueden mejorar su comprensión de las soluciones de los problemas de valor de límite inicial. Para ser específicos, considere la solución formal
\[u(x,t)=\sum_{n=1}^\infty \alpha_ne^{-n^2\pi^2a^2t/L^2}\sin{n\pi x\over L},\nonumber\]
de la Ecuación\ ref {eq:12.1.4}, donde
\[S(x)=\sum_{n=1}^\infty \alpha_n \sin{n\pi x \over L}\nonumber\]
es la serie sinusoidal de Fourier de\(f\) on\([0,L]\). Considere la\(m\) -ésima suma parcial
\[\label{eq:12.1.12} u_m(x,t)=\sum_{n=1}^m \alpha_ne^{-n^2\pi^2a^2t/L^2}\sin{n\pi x\over L}.\]
Para varios valores fijos de\(t\) (incluyendo\(t=0\)), gráfico\(u_m(x,t)\) versus\(t\). En algunos casos puede ser útil graficar las curvas correspondientes a los diversos valores de\(t\) en los mismos ejes en otros casos es posible que desee graficar las diversas curvas sucesivamente (para aumentar los valores de\(t\)), y crear una película primitiva en su monitor. Repita este experimento para varios valores de\(m\), para comparar cómo dependen los resultados\(m\) para valores pequeños y grandes de\(t\). No obstante, hay que tener en cuenta que los significados de “pequeño” y “grande” en este caso dependen de las constantes\(a^2\) y\(L^2\). Una buena manera de manejar esto es reescribir la ecuación\ ref {eq:12.1.12} como
\[u_m(x,t)=\sum_{n=1}^m \alpha_ne^{-n^2\tau}\sin{n\pi x\over L},\nonumber\]
donde
\[\label{eq:12.1.13} \tau={\pi^2a^2t\over L^2},\]
y gráfico\(u_m\) versus\(x\) para valores seleccionados de\(\tau\).
Estos comentarios también se aplican a las situaciones consideradas en Definiciones 12.1.3 - 12.1.5 , excepto que la Ecuación\ ref {eq:12.1.13} debe ser reemplazada por
\[\tau={\pi^2a^2t\over 4L^2},\nonumber\]
en Definiciones 12.1.4 y 12.1.5 .


