13.2: Problemas de Sturm-Liouville
- Page ID
- 115016
En esta sección consideramos problemas de valor propio de la forma
\[\label{eq:13.2.1} P_{0}(x)y''+P_{1}(x)y'+P_{2}(x)y+ \lambda R(x)y=0,\quad B_{1}(y)=0,\quad B_{2}(y)=0,\]
donde
\[B_{1}(y)=\alpha y(a)+\beta y'(a) \quad \text{and} \quad B_{2}(y)=\rho y(b)+\delta y'(b). \nonumber \]
Al igual que en la Sección 13.1\(\alpha\),\(\beta\),\(\rho\),, y\(\delta\) son números reales, con
\[\alpha^{2}+\beta^{2}>0 \quad \text{and} \quad \rho^{2}+\delta^{2}>0, \nonumber \]
\(P_{0}\),\(P_{1}\)\(P_{2}\), y\(R\) son continuos, y\(P_{0}\) y\(R\) son positivos en\([a,b]\).
Decimos que\(\lambda\) es un valor propio de la Ecuación\ ref {eq:13.2.1} si la Ecuación\ ref {eq:13.2.1} tiene una solución no trivial\(y\). En este caso,\(y\) es una función propia asociada con\(\lambda\), o una\(\lambda\) - función propia. Resolver el problema del valor propio significa encontrar todos los valores propios y las funciones propias asociadas de la ecuación\ ref {eq:13.2.1}.
Resolver el problema del valor propio
\[\label{eq:13.2.2} y''+3y'+2y+\lambda y=0,\quad y(0)=0,\quad y(1)=0.\]
Solución
La ecuación característica de la ecuación\ ref {eq:13.2.2} es
\[r^{2}+3r+2+\lambda=0, \nonumber \]
con ceros
\[r_{1}=\frac{-3+\sqrt{1-4\lambda}}{2} \quad \text{and} \quad r_{2}=\frac{-3-\sqrt{1-4\lambda}}{2}. \nonumber \]
Si\(\lambda<1/4\) entonces\(r_{1}\) y\(r_{2}\) son reales y distintos, entonces la solución general de la ecuación diferencial en la Ecuación\ ref {eq:13.2.2} es
\[y=c_{1}e^{r_{1}t}+c_{2}e^{r_{2}t}. \nonumber \]
Las condiciones de contorno requieren que
\[\begin{aligned} c_{1}\phantom{e^{r_{1}}}+c_{2}\phantom{e^{r_{2}}}&=0\\ c_{1}e^{r_{1}}+c_{2}e^{r_{2}}&=0.\end{aligned}\]
Dado que el determinante de este sistema es\(e^{r_{2}}-e^{r_{1}}\ne0\), el sistema sólo tiene la solución trivial. Por lo tanto,\(\lambda\) no es un valor propio de la Ecuación\ ref {eq:13.2.2}.
Si\(\lambda=1/4\) entonces\(r_{1}=r_{2}=-3/2\), entonces la solución general de la Ecuación\ ref {eq:13.2.2} es
\[y=e^{-3x/2}(c_{1}+c_{2}x). \nonumber \]
La condición de límite lo\(y(0)=0\) requiere\(c_{1}=0\), así\(y=c_{2}xe^{-3x/2}\) y la condición de límite lo\(y(0)\) requiere\(c_{2}=0\). Por lo tanto,\(\lambda=1/4\) no es un valor propio de la Ecuación\ ref {eq:13.2.2}.
Si\(\lambda>1/4\) entonces
\[r_{1}=-\frac{3}{2}+i\omega \quad \text{and} \quad r_{2}=-\frac{3}{2}-i\omega, \nonumber \]
con
\[\label{eq:13.2.3} \omega =\frac{\sqrt{4\lambda-1}}{2} \quad \text{or equivalently} \quad \lambda=\frac{1+4\omega^{2}}{4}.\]
En este caso la solución general de la ecuación diferencial en la Ecuación\ ref {eq:13.2.2} es
\[y=e^{-3x/2}(c_{1}\cos\omega x+c_{2}\sin\omega x). \nonumber \]
La condición de límite\(y(0)=0\) requiere eso\(c_{1}=0\), así\(y=c_{2}e^{-3x/2}\sin\omega x\), que se mantiene con\(c_{2}\ne0\) if y solo si\(\omega=n\pi\), donde\(n\) es un entero. Podemos suponer que\(n\) es un entero positivo. (¿Por qué?). De la ecuación\ ref {eq:13.2.3}, los valores propios son\(\lambda_{n}=(1+4n^{2}\pi^{2})/4\), con funciones propias asociadas
\[y_{n}=e^{-3x/2}\sin n\pi x,\quad n=1,2,3,\dots. \nonumber \]
Resolver el problema del valor propio
\[\label{eq:13.2.4} x^{2}y''+xy'+\lambda y=0,\quad y(1)=0,\quad y(2)=0. \]
Solución
Si\(\lambda=0\), la ecuación diferencial en la Ecuación\ ref {eq:13.2.4} se reduce a\(x(xy')'=0\), entonces\(xy'=c_{1}\),
\[y'=\frac{c_{1}}{x}, \quad \text{and} \quad y=c_{1}\ln x+c_{2}. \nonumber \]
La condición límite lo\(y(1)=0\) requiere\(c_{2}=0\), entonces\(y=c_{1}\ln x\). La condición límite lo\(y(2)=0\) requiere\(c_{1}\ln2=0\), entonces\(c_{1}=0\). Por lo tanto cero no es un valor propio de la Ecuación\ ref {eq:13.2.4}.
Si\(\lambda<0\), escribimos\(\lambda=-k^{2}\) con\(k>0\), entonces Ecuación\ ref {eq:13.2.4} se convierte
\[x^{2}y''+xy'-k^{2}y=0, \nonumber \]
una ecuación de Euler (Sección 7.4) con ecuación indicial
\[r^{2}-k^{2}=(r-k)(r+k)=0. \nonumber \]
Por lo tanto
\[y=c_{1}x^{k}+c_{2}x^{-k}. \nonumber \]
Las condiciones de contorno requieren que
\[\begin{aligned} \phantom{2^{k}}c_{1}+\phantom{2^{-k}}c_{2}&=0 \\ 2^{k}c_{1}+2^{-k}c_{2}&=0.\end{aligned}\]
Dado que el determinante de este sistema es\(2^{-k}-2^{k}\ne0\),\(c_{1}=c_{2}=0\). Por lo tanto, la Ecuación\ ref {eq:13.2.4} no tiene valores propios negativos.
Si\(\lambda>0\) escribimos\(\lambda=k^{2}\) con\(k>0\). Entonces la Ecuación\ ref {eq:13.2.4} se convierte
\[x^{2}y''+xy' +k^{2}y=0, \nonumber \]
una ecuación de Euler con ecuación indicial
\[r^{2}+k^{2}=(r-ik)(r+ik)=0, \nonumber \]
entonces
\[y=c_{1}\cos(k\ln x)+c_{2}\sin(k\ln x). \nonumber \]
La condición de límite lo\(y(1)=0\) requiere\(c_{1}=0\). Por lo tanto\(y=c_{2}\sin(k\ln x)\). Esto se mantiene con\(c_{2}\ne0\) si y solo si\(k=n\pi/\ln 2\), donde\(n\) es un entero positivo. Por lo tanto, los valores propios de la Ecuación\ ref {eq:13.2.4} son\(\lambda_{n}=(n\pi/\ln2)^{2}\), con funciones propias asociadas
\[y_{n}=\sin\left(\frac{n\pi}{\ln2}\ln x\right),\quad n=1,2,3,\dots. \nonumber \]
Para fines teóricos, es útil reescribir la ecuación diferencial en la Ecuación\ ref {eq:13.2.1} en una forma diferente, proporcionada por el siguiente teorema.
Si\(P_{0},\)\(P_{1},\)\(P_{2},\) y\(R\) son continuos y\(P_{0}\) y\(R\) son positivos en un intervalo cerrado\([a,b],\) entonces la ecuación
\[\label{eq:13.2.5} P_{0}(x)y''+P_{1}(x)y'+P_{2}(x)y+\lambda R(x)y=0\]
se puede reescribir como
\[\label{eq:13.2.6} (p(x)y')'+q(x)y+\lambda r(x)y=0,\]
donde\(p\)\(p'\),\(q\) y\(r\) son continuos y\(p\) y\(r\) son positivos en\([a,b].\)
- Prueba
-
Comenzamos reescribiendo la ecuación\ ref {eq:13.2.5} como
\[\label{eq:13.2.7} y''+u(x)y'+v(x)y+\lambda R_{1}(x)y=0,\]
con\(u=P_{1}/P_{0}\),\(v=P_{2}/P_{0}\), y\(R_{1}=R/P_{0}\). (Tenga en cuenta que\(R_{1}\) es positivo en\([a,b]\).) Ahora vamos\(p(x)=e^{U(x)}\), donde\(U\) está cualquier antiderivado de\(u\). Entonces\(p\) es positivo\([a,b]\) y, ya que\(U'=u\),
\[\label{eq:13.2.8} p'(x)=p(x)u(x)\]
es continuo en\([a,b]\). Multiplicando la ecuación\ ref {eq:13.2.7} por\(p(x)\) rendimientos
\[\label{eq:13.2.9} p(x)y''+p(x)u(x)y'+p(x)v(x)y+\lambda p(x)R_{1}(x)y=0.\]
Dado que\(p\) es positivo\([a,b]\), esta ecuación tiene las mismas soluciones que la Ecuación\ ref {eq:13.2.5}. De la ecuación\ ref {eq:13.2.8},
\[(p(x)y')'=p(x)y''+p'(x)y'=p(x)y''+p(x)u(x)y', \nonumber \]
así que la Ecuación\ ref {eq:13.2.9} se puede reescribir como en la Ecuación\ ref {eq:13.2.6}, con\(q(x)=p(x)v(x)\) y\(r(x)=p(x)R_{1}(x)\). Esto completa la prueba.
Se debe entender a lo largo del resto de esta sección que\(p\),\(q\), y\(r\) tener las propiedades establecidas en el Teorema 13.2.1 . Además, cada vez que escribimos\(Ly\) en una declaración general, nos referimos a
\[Ly=(p(x)y')'+q(x)y. \nonumber \]
La ecuación diferencial Ecuación\ ref {eq:13.2.6} se llama ecuación de Sturm - Liouville, y el problema del valor propio
\[\label{eq:13.2.10} (p(x)y')'+q(x)y+\lambda r(x)y=0,\quad B_{1}(y)=0,\quad B_{2}(y)=0,\]
que es equivalente a la Ecuación\ ref {eq:13.2.1}, se llama un problema de Sturm-Liouville.
Reescribir el problema del valor propio
\[\label{eq:13.2.11} y''+3y'+(2+\lambda)y=0,\quad y(0)=0,\quad y(1)=0\]
del Teorema 13.2.1 como un problema de Sturm-Liouville.
Solución
Comparando la Ecuación\ ref {eq:13.2.11} con la Ecuación\ ref {eq:13.2.7} demuestra que\(u(x)=3\), así tomamos\(U(x)=3x\) y\(p(x)=e^{3x}\). Multiplicar la ecuación diferencial en la Ecuación\ ref {eq:13.2.11} por\(e^{3x}\) rendimientos
\[e^{3x}(y''+3y')+2e^{3x}y+\lambda e^{3x}y=0. \nonumber \]
Desde
\[e^{3x}(y''+3y')=(e^{3x}y')', \nonumber \]
La ecuación\ ref {eq:13.2.11} es equivalente al problema de Sturm—Liouville
\[\label{eq:13.2.12} (e^{3x}y')'+2e^{3x}y+\lambda e^{3x}y=0,\quad y(0)=0,\quad y(1)=0.\]
Reescribir el problema del valor propio
\[\label{eq:13.2.13} x^{2}y''+xy'+\lambda y=0,\quad y(1)=0,\quad y(2)=0\]
del Teorema 13.2.2 como un problema de Sturm-Liouville.
Solución
Dividiendo la ecuación diferencial en la Ecuación\ ref {eq:13.2.13} por\(x^{2}\) rendimientos
\[y''+\frac{1}{x}y'+\frac{\lambda}{x^{2}}y=0. \nonumber \]
Comparando esto con la Ecuación\ ref {eq:13.2.7} demuestra que\(u(x)=1/x\), así tomamos\(U(x)=\ln x\) y\(p(x)=e^{\ln x}=x\). Multiplicar la ecuación diferencial por\(x\) rendimientos
\[xy''+y'+\frac{\lambda}{x}y=0. \nonumber \]
Desde
\[xy''+y'=(xy')', \nonumber \]
La ecuación\ ref {eq:13.2.13} es equivalente al problema de Sturm—Liouville
\[\label{eq:13.2.14} (xy')'+\frac{\lambda}{x}y=0,\quad y(1)=0,\quad y(2)=0.\]
Los problemas 1—4 de la Sección 11.1 son problemas de Sturm—Liouville. (El problema 5 no lo es, aunque algunos autores utilizan una definición de problema de Sturm-Liouville que sí lo incluye). Pudimos encontrar explícitamente los valores propios de los Problemas 1-4 porque en cada problema los coeficientes en las condiciones límite satisfacen\(\alpha\beta=0\) y\(\rho\delta=0\); es decir, cada condición límite involucra a uno\(y\) o\(y'\), pero no a ambos. Si esto no es cierto entonces los valores propios no pueden expresarse en general exactamente por fórmulas simples; más bien, los valores aproximados deben obtenerse por solución numérica de ecuaciones derivadas al requerir que los determinantes de ciertos\(2\times 2\) sistemas de ecuaciones homogéneas sean cero. Para aplicar los métodos numéricos de manera efectiva, se deben utilizar métodos gráficos para determinar las ubicaciones aproximadas de los ceros de estos determinantes. Entonces los ceros pueden ser calculados con precisión por métodos numéricos.
Resolver el problema de Sturm—Liouville
\[\label{eq:13.2.15} y''+\lambda y=0, \quad y(0)+y'(0)=0,\quad y(1)+3y'(1)=0.\]
Solución
Si\(\lambda=0\), la ecuación diferencial en la Ecuación\ ref {eq:13.2.15} se reduce a\(y''=0\), con solución general\(y=c_{1}+c_{2}x\). Las condiciones de contorno requieren que
\[\begin{aligned} c_{1}+\phantom{4}c_{2}&=0\\ c_{1}+4c_{2}&=0,\end{aligned}\]
así\(c_{1}=c_{2}=0\). Por lo tanto cero no es un valor propio de la Ecuación\ ref {eq:13.2.15}.
Si\(\lambda<0\), escribimos\(\lambda=-k^{2}\) dónde\(k>0\), y la ecuación diferencial en la Ecuación\ ref {eq:13.2.15} se convierte\(y''-k^{2}y=0\), con solución general
\[\label{eq:13.2.16} y=c_{1}\cosh kx+c_{2}\sinh kx,\]
entonces
\[y'=k(c_{1}\sinh kx+c_{2}\cosh kx). \nonumber \]
Las condiciones de contorno requieren que
\[\label{eq:13.2.17} \begin{array}{c}{c_{1}+kc_{2}=0}\\{(\cosh k+3k\sinh k)c_{1}+(\sinh k+3k\cosh k)c_{2}=0}\end{array}\]
El determinante de este sistema es
\[\begin{aligned} D_{N}(k)&= \left|\begin{array}{cccccc} 1&k\\ \cosh k+3k\sinh k&\sinh k+3k \cosh k \end{array}\right| \\ &= (1-3k^{2})\sinh k+2k \cosh k.\end{aligned}\]
Por lo tanto el sistema Ecuación\ ref {eq:13.2.17} tiene una solución no trivial si y solo si\(D_{N}(k)=0\) o, de manera equivalente,
\[\label{eq:13.2.18} \tanh k=-\frac{2k}{1-3k^{2}}.\]
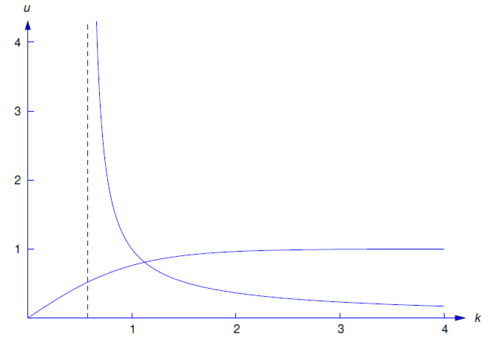
La gráfica del lado derecho (Figura 13.2.1 ) tiene una asíntota vertical en\(k=1/\sqrt{3}\). Ya que los dos lados tienen signos diferentes si\(k<1/\sqrt{3}\), esta ecuación no tiene solución en\((0,1/\sqrt{3})\). La Figura 13.2.1 muestra las gráficas de los dos lados de la Ecuación\ ref {eq:13.2.18} en un intervalo a la derecha de la asíntota vertical, que se indica mediante la línea discontinua. Se puede ver que las dos curvas se cruzan cerca\(k_{0}=1.2\), dado este estmate, se puede utilizar Newtons para calcular con\(k_{0}\) mayor precisión. Nosotros computamos\(k_{0}\approx 1.1219395\). Por lo tanto\(-k_{0}^{2}\approx -1.2587483\) es un valor propio de la Ecuación\ ref {eq:13.2.15}. De la Ecuación\ ref {eq:13.2.16} y la primera ecuación en la Ecuación\ ref {eq:13.2.17},
\[y_{0}=k_{0}\cosh k_{0}x-\sinh k_{0}x. \nonumber \]
Si\(\lambda>0\) escribimos\(\lambda=k^{2}\) donde\(k>0\), y la ecuación diferencial en la Ecuación\ ref {eq:13.2.15} se convierte\(y''+k^{2}y=0\), con solución general
\[\label{eq:13.2.19} y= \cos kx + c_{2}\sin kx,\]
entonces
\[y'=k(-c_{1}\sin kx+c_{2}\cos kx). \nonumber \]
Las condiciones de contorno requieren que
\[\label{eq:13.2.20} \begin{array}{c} {c_{1}+kc_{2}=0}\\ {(\cos k-3k\sin k)c_{1}+(\sin k+3k\cos k)c_{2}=0.} \end{array}\]
El determinante de este sistema es
\[\begin{aligned} D_{P}(k)&= \left|\begin{array}{cccccc} 1&k\\ \cos k-3k\sin k&\sin k+3k \cos k \end{array}\right| \\ &= (1+3k^{2})\sin k+2k \cos k.\end{aligned}\]
El sistema Ecuación\ ref {eq:13.2.20} tiene una solución no trivial si y solo si\(D_{P}(k)=0\) o, de manera equivalente,
\[\tan k=-\frac{2k}{1+3k^{2}}. \nonumber \]
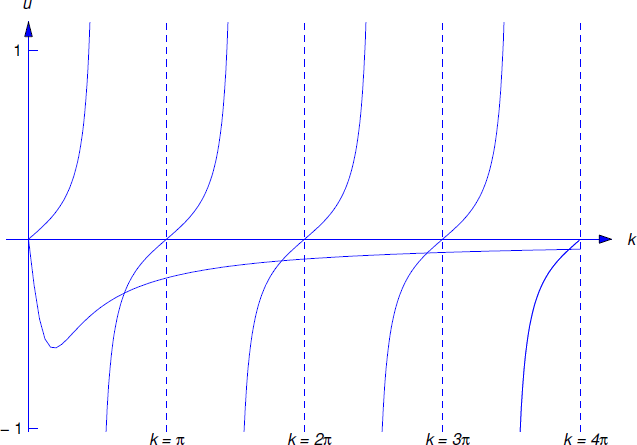
La figura 13.2.2 muestra las gráficas de los dos lados de esta ecuación. Se puede ver en la figura que las gráficas se cruzan en infinitamente muchos puntos\(k_{n}\approx n\pi\) (\(n=1\),\(2\),\(3\),...), donde el error en esta aproximación se acerca a cero como\(n\to\infty\). Dada esta estimación, puedes usar el método de Newton para calcular con\(k_{n}\) mayor precisión. Nosotros computamos
\[\begin{aligned} k_{1}&\approx \phantom{1}2.9256856,\\ k_{2}&\approx \phantom{1} 6.1765914,\\ k_{3}&\approx \phantom{1} 9.3538959,\\ k_{4}&\approx 12.5132570.\end{aligned}\]
Las estimaciones de los valores propios correspondientes\(\lambda_{n}=k_{n}^{2}\) son
\[\begin{aligned} \lambda_{1}&\approx \phantom{15} 8.5596361,\\ \lambda_{2}&\approx \phantom{5} 38.1502809,\\ \lambda_{3}&\approx \phantom{5} 87.4953676,\\ \lambda_{4}&\approx 156.5815998.\end{aligned}\]
De la Ecuación\ ref {eq:13.2.19} y la primera ecuación en la Ecuación\ ref {eq:13.2.20},
\[y_{n}=k_{n}\cos k_{n}x-\sin k_{n}x \nonumber \]
es una función propia asociada con\(\lambda_{n}\)
Dado que las ecuaciones diferenciales en la Ecuación\ ref {eq:13.2.12} y la Ecuación\ ref {eq:13.2.14} son más complicadas que las de la Ecuación\ ref {eq:13.2.11} y la Ecuación\ ref {eq:13.2.13} respectivamente, ¿cuál es el punto del Teorema 13.2.1 ? El punto es este: para resolver un problema específico, puede ser mejor tratarlo directamente, como lo hicimos en Ejemplos 13.2.1 y 13.2.2 ; sin embargo, veremos que transformando el problema general de valores propios Ecuación\ ref {eq:13.2.1} al Sturm—Liouville problema Ecuación\ ref {eq:13.2.10} conduce a resultados aplicables a todos los problemas de valor propio de la forma Ecuación\ ref {eq:13.2.1}.
Si
\[Ly=(p(x)y')'+q(x)y \nonumber \]
\(u\)y\(v\) son dos veces continuamente funciones en\([a,b]\) que satisfacen las condiciones del límite\(B_{1}(y)=0\) y\(B_{2}(y)=0,\) luego
\[\label{eq:13.2.21} \int_{a}^{b}[u(x)Lv(x)-v(x)Lu(x)]\,dx=0.\]
- Prueba
-
Integración por rendimientos de piezas
\[\begin{aligned} \int_{a}^{b}[u(x)Lv(x)-v(x)Lu(x)]\,dx&= \int_{a}^{b}[u(x)(p(x)v'(x))'-v(x)(p(x)u'(x))']\,dx\\ &= p(x)[u(x)v'(x)-u'(x)v(x)]\bigg|_{a}^{b}\\ &-\int_{a}^{b}p(x)[u'(x)v'(x)-u'(x)v'(x)]\,dx.\end{aligned}\]
Dado que la última integral es igual a cero,
\[\label{eq:13.2.22} \int_{a}^{b}[u(x)Lv(x)-v(x)Lu(x)]\,dx = p(x)[u(x)v'(x)-u'(x)v'(x)]\bigg|_{a}^{b}.\]
Por suposición,\(B_{1}(u)=B_{1}(v)=0\) y\(B_{2}(u)=B_{2}(v)=0\). Por lo tanto
\[\begin{aligned} \alpha u(a)+\beta u'(a)&=0\\ \alpha v(a)+\beta v'(a)&=0\\ \end{aligned} \quad \quad \text{and} \quad \quad \begin{gathered} \rho u(b)+\delta u'(b)=0\phantom{.}\\ \rho v(b)+\delta v'(b)=0. \end{gathered}\]
Dado que\(\alpha^{2}+\beta^{2}>0\) y\(\rho^{2}+\delta^{2}>0\), los determinantes de estos dos sistemas deben ser ambos cero; es decir,
\[u(a)v'(a)-u'(a)v(a)=u(b)v'(b)-u'(b)v(b)=0. \nonumber \]
Esto y la Ecuación\ ref {eq:13.2.22} implican la Ecuación\ ref {eq:13.2.21}, que completa la prueba.
El siguiente teorema muestra que un problema de Sturm-Liouville no tiene valores propios complejos.
Si\(\lambda=p+qi\) con\(q\ne0\) entonces el problema del valor límite
\[Ly+\lambda r(x)y=0,\quad B_{1}(y)=0,\quad B_{2}(y)=0 \nonumber \]
tiene sólo la solución trivial.
- Prueba
-
Para que este teorema tenga sentido, debemos considerar soluciones de valor complejo de
\[\label{eq:13.2.23} Ly+(p+iq)r(x,y)y=0.\]
Si\(y=u+iv\) dónde\(u\) y\(v\) son de valor real y dos veces diferenciables, definimos\(y'=u'+iv'\) y\(y''=u''+iv''\). Decimos que\(y\) es una solución de la Ecuación\ ref {eq:13.2.23} si las partes real e imaginaria del lado izquierdo de la Ecuación\ ref {eq:13.2.23} son ambas cero. Dado que\(Ly=(p(x)'y)'+q(x)y\) y\(p\)\(q\), y\(r\) son de valor real,
\[\begin{aligned} Ly+\lambda r(x)y&=L(u+iv)+(p+iq)r(x)(u+iv)\\ &=Lu+r(x)(pu-qv)+i[Lv+r(x)(pu+qv)],\end{aligned}\]
así que\(Ly+\lambda r(x)y=0\) si y solo si
\[\begin{aligned} Lu+r(x)(pu-qv)&=0\\ Lv+r(x)(qu+pv)&=0.\end{aligned}\]
Multiplicar la primera ecuación por\(v\) y la segunda por\(u\) rendimientos
\[\begin{aligned} vLu+r(x)(puv-qv^{2})&=0\\ uLv+r(x)(qu^{2}+puv)&=0.\end{aligned}\]
Restar la primera ecuación de los segundos rendimientos
\[uLv-vLu+qr(x)(u^{2}+v^{2})=0, \nonumber \]
entonces
\[\label{eq:13.2.24} \int_{a}^{b}[u(x)Lv(x)-v(x)Lu(x)]\,dx+ \int_{a}^{b}r(x)[u^{2}(x)+v^{2}(x)]\,dx=0.\]
Desde
\[B_{1}(y)=B_{1}(u+iv)=B_{1}(u)+iB_{1}(v) \nonumber \]
y
\[B_{2}(y)=B_{2}(u+iv)=B_{2}(u)+iB_{2}(v), \nonumber \]
\(B_{1}(y)=0\)e\(B_{2}(y)=0\) implica que
\[B_{1}(u)=B_{2}(u)=B_{1}(v)=B_{2}(v)=0. \nonumber \]
Por lo tanto, el teorema 13.2.2 implica que la primera integral en la Ecuación\ ref {eq:13.2.24} es igual a cero, así que la Ecuación\ ref {eq:13.2.24} reduce a
\[q\int_{a}^{b}r(x)[u^{2}(x)+v^{2}(x)]\,dx =0.\nonumber \]
Dado que\(r\) es positivo sobre\([a,b]\) y\(q\ne0\) por suposición, esto implica eso\(u\equiv0\) y así\(v\equiv0\) sucesivamente\([a,b]\). Por lo tanto\([a,b]\),\(y\equiv0\) en el que se completa la prueba.
Si\(\lambda_{1}\) y\(\lambda_{2}\) son valores propios distintos del problema de Sturm-Liouville
\[\label{eq:13.2.25} Ly+\lambda r(x)y=0,\quad B_{1}(y)=0,\quad B_{2}(y)=0\]
con funciones propias asociadas\(u\) y\(v\)\(,\) respectivamente
\[\label{eq:13.2.26} \int_{a}^{b}r(x)u(x)v(x)\,dx=0.\]
- Prueba
-
Dado que\(u\) y\(v\) satisfacer las condiciones de límite en la ecuación\ ref {eq:13.2.25}, el teorema 13.2.2 implica que
\[\int_{a}^{b}[u(x)Lv(x)-v(x)Lu(x)]\,dx=0. \nonumber \]
Desde\(Lu=-\lambda_{1}ru\) y\(Lv=-\lambda_{2}rv\), esto implica que
\[(\lambda_{1}-\lambda_{2})\int_{a}^{b}r(x)u(x)v(x)\,dx=0. \nonumber \]
Ya que\(\lambda_{1}\ne\lambda_{2}\), esto implica la Ecuación\ ref {eq:13.2.26}, que completa la prueba.
Si\(u\) y\(v\) son funciones integrables en\([a,b]\) y
\[\int_{a}^{b} r(x)u(x)v(x)\,dx=0, \nonumber \]
decimos eso\(u\) y\(v\) ortogonal sobre\([a,b]\) con respecto a\(r=r(x)\).
El teorema 13.1.1 implica el siguiente teorema.
Si\(u\not\equiv0\) y\(v\) ambos satisfacen
\[Ly+\lambda r(x)y=0,\quad B_{1}(y)=0,\quad B_{2}(y)=0, \nonumber \]
luego\(v=cu\) por alguna constante\(c.\)
Ahora hemos probado partes del siguiente teorema. Una prueba completa está más allá del alcance de este libro.
El conjunto de todos los valores propios del problema de Sturm—Liouville
\[Ly+\lambda r(x)y=0,\quad B_{1}(y)=0,\quad B_{2}(y)=0 \nonumber \]
se puede pedir como
\[\lambda_{1}<\lambda_{2}<\cdots<\lambda_{n}<\cdots, \nonumber \]
y
\[\lim_{n\to\infty} \lambda_{n}=\infty. \nonumber \]
Para cada\(n,\) if\(y_{n}\) es una función\(\lambda_{n}\) -eigenarbitraria\(,\) entonces cada\(\lambda_{n}\) -función propia es un múltiplo constante de\(y_{n}.\) If\(m\ne n,\)\(y_{m}\) y\(y_{n}\) son ortogonales\([a,b]\) con respecto a\(r=r(x);\) eso es\(,\)
\[\label{eq:13.2.27} \int_{a}^{b} r(x)y_{m}(x)y_{n}(x)\,dx=0.\]
Es posible que desee verificar la ecuación\ ref {eq:13.2.27} para las funciones propias obtenidas en los ejemplos 13.2.1 y 13.2.2 .
En conclusión, mencionamos el siguiente teorema. La prueba está más allá del alcance de este libro.
\(\lambda_{1}<\lambda_{2}<\cdots<\lambda_{n}<\cdots\)Dejen ser los valores propios del problema de Sturm-Liouville
\[Ly+\lambda r(x)y=0,\quad B_{1}(y)=0,\quad B_{2}(y)=0,\nonumber \]
con vectores propios asociados\(y_{1},\)\(y_{2},\)...,\(y_{n},\)...\(.\) Supongamos que\(f\) es liso por partes (Definición 11.2.3) on\([a,b].\) Para cada\(n,\) let
\[c_{n}=\frac{ \int_{a}^{b} r(x)f(x)y_{n}(x) \, dx}{ \int_{a}^{b} r(x)y_{n}^{2}(x)\,dx}.\nonumber \]
Entonces
\[\frac{f(x-)+f(x+)}{2}=\sum_{n=1}^{\infty}c_{n}y_{n}(x) \nonumber \]
para todos\(x\) en el intervalo abierto\((a,b).\)


