1.0: Introducción
- Page ID
- 118049
Prefacio
Estas notas de conferencia se proponen como una introducción directa a las ecuaciones diferenciales parciales que pueden servir como libro de texto para estudiantes de pregrado y posgrado principiantes.
Para lectura adicional recomendamos los siguientes libros: W. I. Smirnov [21], I. G. Petrovski [17], P. R. Garabedian [8], W. A. Strauss [23], F. John [10], L. C. Evans [5] y R. Courant y D. Hilbert [4] y D. Gilbarg y N. S. Trudinger [9]. De algunos de estos libros se tomó algún material de estas notas de conferencia.
Introducción
Las ecuaciones diferenciales ordinarias y parciales ocurren en muchas aplicaciones. Una ecuación diferencial ordinaria es un caso especial de una ecuación diferencial parcial pero el comportamiento de las soluciones es bastante diferente en general causado por el hecho de que las funciones para las que estamos viendo son funciones de más de una variable independiente.
Ecuación
$$F (x, y (x), y' (x),\ ldots, y^ {(n)}) =0\]
es una ecuación diferencial ordinaria de orden n-ésimo para la función desconocida\(y(x)\), donde\(F\) se da.
Un problema importante para las ecuaciones diferenciales ordinarias es el problema del valor inicial
\ begin {eqnarray*}
y' (x) &=&f (x, y (x))\\
y (x_0) &=&y_0\,
\ end {eqnarray*}
donde\(f\) es una función real dada de dos variables\(x\),\(y\) y\(x_0,\),\( y_0\) se les dan números reales.
Teorema de Picard-Lindelöf. Supongamos que
(i)\(f(x,y)\) es continuo en un rectángulo
$$Q=\ {(x, y)\ in {{\ mathbb R} ^2}:\ |x-x_0|<a,\ |y-y_0|<b\}. $$
(ii) Hay una constante\(K\) tal que\(|f(x,y)|\le K\) para todos\((x,y) \in Q\).
(ii) Condición de Lipschitz: Hay una constante\(L\) tal que
$$|f (x, y_2) -f (x, y_1) |\ le L|y_2-y_1|$$
para todos\((x,y_1), (x,y_2)\).
Figura 1.0.1: Problema de valor inicial
Entonces existe una solución única\(y\in C^1(x_0-\alpha,x_0+\alpha)\) del problema de valor inicial anterior, donde\(\alpha=\min (b/K,a)\).
La ecuación diferencial lineal ordinaria
$$y^ {(n)} +a_ {n-1} (x) y^ {(n-1)} +\ lpuntos a_1 (x) y'+a_0 (x) y=0,\]
donde\(a_j\) están las funciones continuas, tiene soluciones exactamente\(n\) linealmente independientes. En contraste con esta propiedad, el diferencial\(u_{xx}+u_{yy}=0\) parcial\({\mathbb R}^2\) tiene infinitamente muchas soluciones linealmente independientes en el espacio lineal\(C^2(\mathbb{R})^2\).
La ecuación diferencial ordinaria de segundo orden
$$y "(x) =f (x, y (x), y' (x))\]
tiene en general una familia de soluciones con dos parámetros libres. Por lo tanto, es natural considerar el problema de valor inicial asociado
\ begin {eqnarray*}
y "(x) &=&f (x, y (x), y' (x))\\
y (x_0) &=&y_0,\ y' (x_0) =y_1,
\ end {eqnarray*}
donde\(y_0\) y\(y_1\) se dan, o para considerar el problema del valor límite
\ begin {eqnarray*}
y "(x) &=&f (x, y (x), y' (x))\\
y (x_0) &=&y_0,\ y (x_1) =y_1.
\ end {eqnarray*}
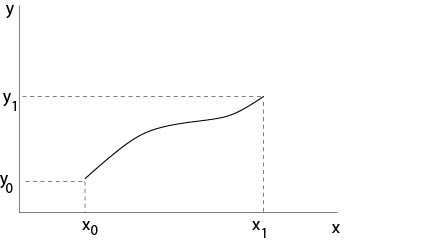
Figura 1.0.2: Problema de valor límite
Los problemas de valor inicial y límite juegan un papel importante también en la teoría de ecuaciones diferenciales parciales. Una ecuación diferencial parcial para la función desconocida\(u(x,y)\) es, por ejemplo
$$F (x, y, u, u_x, u_y, u_ {xx}, u_ {xy}, u_ {yy}) =0,\]
donde se da\(F\) la función. Esta ecuación es de segundo orden.
Se dice que una ecuación es de orden n-ésimo si la derivada más alta que ocurre es de orden\(n\).
Se dice que una ecuación es lineal si la función desconocida y sus derivadas son lineales en\(F\). Por ejemplo,
$$a (x, y) u_x+b (x, y) u_y+c (x, y) u=f (x, y),\]
donde las funciones\(a\),\(b\),\(c\) y\(f\) se dan, es una ecuación lineal de primer orden.
Se dice que una ecuación es cuasilineal si es lineal en las derivadas más altas. Por ejemplo,
$$a (x, y, u, u_x, u_y) u_ {xx} +b (x, y, u, u_x, u_y) u_ {xy} +c (x, y, u, u_x, u_y) u_ {yy} =0\]
es una ecuación cuasilineal de segundo orden.