1.1: Ejemplos

Última actualización
Guardar como PDF

Page ID: 118059

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Ejemplo 1.1.1:

$u_y=0$, donde$u=u(x,y)$. Todas las funciones$u=w(x)$ son soluciones.

Ejemplo 1.1.2:

$u_x=u_y$, donde$u=u(x,y)$. Un cambio de coordenadas transforma esta ecuación en una ecuación del primer ejemplo. Establecer$\xi=x+y,\ \eta=x-y$, entonces
$$
u (x, y) =u\ izquierda (\ frac {\ xi+\ eta} {2},\ frac {\ xi-\ eta} {2}\ derecha) =:v (\ xi,\ eta).
$$
Supongamos$u\in C^1$, entonces
$$
v_\ eta=\ frac {1} {2} (u_x-u_y).
$$
Si$u_x=u_y$, entonces$v_\eta=0$ y viceversa, así$v=w(\xi)$ son soluciones para$C^1$ -funciones arbitrarias$w(\xi)$. En consecuencia, tenemos una gran clase de soluciones de la ecuación diferencial parcial original:$u=w(x+y)$ con una$C^1$ función arbitraria$w$.

Ejemplo 1.1.3:

Una condición necesaria y suficiente tal que para determinadas$C^1$ -funciones$M,\ N$ la integral
$$
\ int_ {P_0} ^ {P_1}\ M (x, y) dx+n (x, y) dy
$$
es independiente de la curva que conecta los puntos$P_0$ con$P_1$ en un simple conectado dominio$\Omega\subset\mathbb{R}^2$ es que la ecuación diferencial parcial (condición de integrabilidad)
$$
m_y=N_x
$$
in$\Omega$.

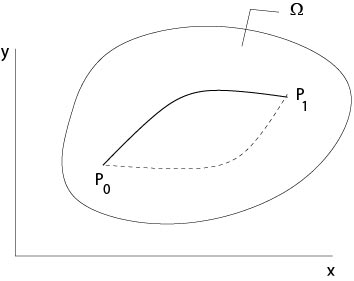
$Independencia del camino$

Figura 1.1.1: Independencia del camino

Esta es una ecuación para dos funciones. Una gran clase de soluciones viene dada por$M=\Phi_x,\ N=\Phi_y$, donde$\Phi(x,y)$ es una$C^2$ función arbitraria. Del teorema de Gauss se deduce que todas estas son$C^1$ soluciones de la ecuación diferencial anterior.

Ejemplo 1.1.4: Método de un multiplicador integrador para un ordinario

diferencial

ecuación

Considere la ecuación diferencial ordinaria
$$
M (x, y) Dx+n (x, y) dy=0
$$
para$C^1$ -funciones dadas$M,\ N$. Entonces buscamos una$C^1$ -función$\mu(x,y)$ tal que$\mu Mdx+\mu Ndy$ sea un diferencial total, es decir, que$(\mu M)_y=(\mu N)_x$ se satisfaga. Esta es una ecuación diferencial parcial lineal de primer orden para$\mu$:
$$
M\ mu_y-N\ mu_x=\ mu (N_x-M_y).
\]

Ejemplo 1.1.5:

Dos$C^1$ -funciones$u(x,y)$ y$v(x,y)$ se dice que son funcionalmente dependientes si
$$
\ det\ left (\ begin {array} {cc} u_x&u_y\\ v_x&v_y\ end {array}\ right) =0,
$$
que es una ecuación diferencial parcial lineal de primer orden para$u$ si$v$ es una$C^1$ función dada. Una gran clase de soluciones viene dada por
$$
u=h (v (x, y)),
$$
donde$H$ es una$C^1$ función arbitraria.

Ejemplo 1.1.6: Ecuaciones de Cauchy-Riemann

Establecer$f(z)=u(x,y)+iv(x,y)$, donde$z=x+iy$ y$u,\ v$ se les dan$C^1(\Omega)$ -funciones. Aquí$\Omega$ hay un dominio en$\mathbb{R}^2$. Si la función$f(z)$ es diferenciable con respecto a la variable compleja$z$ entonces$u,\ v$ satisfacer las ecuaciones de Cauchy-Riemann
$$
u_x=v_y,\\ u_y=-v_x.
$$
Se sabe a partir de la teoría de funciones de una variable compleja que la parte real$u$ y la parte imaginaria$v$ de una función diferenciable$f(z)$ son soluciones de la ecuación de Laplace
$$
\ triángulo u=0,\\\ triángulo v=0,
$$
donde$\triangle u= u_{xx}+u_{yy}$.

Ejemplo 1.1.7: Potencial Newton

El potencial Newton
$$
u=\ frac {1} {\ sqrt {x^2+y^2+z^2}}
$$
es una solución de la ecuación de Laplace en$\mathbb{R}^3\setminus{(0,0,0)}$, es decir, de
$$
u_ {xx} +u_ {yy} +u_ {zz} =0.
\]

Ejemplo 1.1.8: Ecuación de calor

Dejar$u(x,t)$ ser la temperatura de un punto$x\in\Omega$ en el tiempo$t$, donde$\Omega\subset\mathbb{R}^3$ es un dominio. Entonces$u(x,t)$ satisface en$\Omega\times[0,\infty)$ la ecuación de calor
$$
u_t=k\ triángulo u,
$$
donde$\triangle u= u_{x_1x_1}+u_{x_2x_2}+u_{x_3x_3}$ y$k$ es una constante positiva. La condición
$$
u (x,0) =u_0 (x),\\ x\ in\ Omega,
$$
donde$u_0(x)$ se da, es una condición inicial asociada a la ecuación de calor anterior. La condición
$$
u (x, t) =h (x, t),\\ x\ in\ parcial\ Omega,\ t\ ge0,
$$
donde$h(x,t)$ se da, es una condición límite para la ecuación de calor.

Si$h(x,t)=g(x)$, es decir,$h$ es independiente de$t$, entonces uno espera que la solución$u(x,t)$ tiende a una función$v(x)$ si$t\to\infty$. Además, resulta que$v$ es la solución del problema del valor límite para la ecuación de Laplace
\ begin {eqnarray*}
\ triángulo v&=&0\\\ mbox {in}\\ Omega\\
v&=&g (x)\\\ mbox {on}\\ parcial\ Omega.
\ end {eqnarray*}

Ejemplo 1.1.9: Ecuación de onda

$alt$
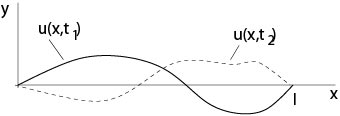
Figura 1.1.2: Cadena oscilante

La ecuación de onda
$$
u_ {tt} =c^2\ triángulo u,
$$
donde$u=u(x,t)$,$c$ es una constante positiva, describe oscilaciones de membranas o de dominios tridimensionales, por ejemplo. En el caso unidimensional
$$
u_ {tt} =c^2 u_ {xx}
$$
describe oscilaciones de una cadena.

Las condiciones iniciales asociadas son
$$
u (x,0) =u_0 (x),\\ u_t (x,0) =u_1 (x),
$$
donde$u_0,\ u_1$ se dan funciones. Así se prescriben la posición inicial y la velocidad inicial.

Si la cadena es finita se describen adicionalmente las condiciones de contorno, por ejemplo
$$
u (0, t) =0,\\ u (l, t) =0\\\ mbox {for all}\ t\ ge 0.
\]

Search

Text Color

Text Size

Margin Size

Font Type