2.5: Teoría Hamilton-Jacobi

La ecuación no lineal (2.4.1) de la sección anterior en una dimensión más es

$$
F (x_1,\ ldots, x_n, x_ {n+1}, z, p_1,\ ldots, p_n, p_ {n+1}) =0.
\]

El contenido de la teoría Hamilton ^{1-Jacobi 2} es la teoría del caso especial

\ begin {ecuación}
\ label {nonlineearham}
F\ equiv p_ {n+1} +H (x_1,\ ldots, x_n, x_ {n+1}, p_1,\ ldots, p_n) =0,
\ end {ecuación}

i. e., la ecuación es lineal en\(p_{n+1}\) y no depende de\(z\) explícitamente.

OBSERVACIÓN. Formalmente, se puede escribir la ecuación (2.4.1)

$$F (x_1,\ ldots, x_n, u, u_ {x_1},\ ldots, u_ {x_n}) =0\]

como una ecuación de tipo (\ ref {nonlinearham}). Establecer\(x_{n+1}=u\) y buscar\(u\) implícitamente de

$$\ phi (x_1,\ ldots, x_n, x_ {n+1}) =const.,\]

donde\(\phi\) es una función que se define por una ecuación diferencial.

Supongamos\(\phi_{x_{n+1}}\not=0\), entonces

\ begin {eqnarray*}
0&=&F (x_1,\ ldots, x_n, u, u_ {x_1},\ ldots, u_ {x_n})\\
&=&F (x_1,\ ldots, x_n, x_ {n+1}, -\ frac {\ phi_ {x_1}} {\ phi_ {x_ {n+1}}},\ lpuntos, -\ frac {\ phi_ {x_n}} {\ phi_ {x_ {n+1}})\\
&=&:G (x_1,\ ldots, x_ {n+1},\ phi_1,\ ldots,\ phi_ {x_ {n+1}}).
\ end {eqnarray*}

Supongamos que\(G_{\phi_{x_{n+1}}}\not=0\), entonces

$$\ phi_ {x_ {n+1}} =H (x_1,\ ldots, x_n, x_ {n+1},\ phi_ {x_1},\ ldots,\ phi_ {x_ {n+1}}).\]

Las ecuaciones características asociadas a (\ ref {nonlinearham}) son

\ begin {eqnarray*}
x_ {n+1} '(\ tau) &=&F_ {p_ {n+1}} =1\\
x_k' (\ tau) &=&F_ {p_k} =H_ {p_k},\ qquad k=1,\ ldots, n\\
z' (\ tau) &=&\ sum_ {l=1} ^ n+1} P_LF_ {p_l} =\ suma_ {l=1} ^NP_LH_ {p_l} +p_ {n+1}\\
&=&\ suma_ {l=1} ^NP_LH_ {p_l} -H\\
p'_ {n+1} (\ tau) &=&-F_ {x_ {n+1}} -f_zp_ {n+1}\\
&=&-F_ {x_ {n+1}}\\
p_k' (\ tau) &=&-F_ {x_k} -f_zp_k\\
&=&-F_ {x_k},\ qquad =1,\ lpuntos, n.
\ end {eqnarray*}

Set\(t:=x_{n+1}\), entonces podemos escribir ecuación diferencial parcial (\ ref {nonlinearham}) como

\ begin {ecuación}
\ label {hamjac}
u_t+h (x, t,\ nabla_xu) =0
\ end {ecuación}
y\(2n\) de las ecuaciones características son
\ begin {eqnarray}
\ label {charhj1}
x' (t) &=&\ nabla_ph (x, t, p)\
\ label {charhj2}
p' (t) &=&-\ Nabla_xH (x, t, p).
\ end {eqnarray}
Aquí está

$$x= (x_1,\ ldots, x_n),\ p= (p_1,\ ldots, p_n).\]

Dejar\(x(t),\ p(t)\) ser una solución de (\ ref {charhj1}) y (\ ref {charhj2}), entonces se deduce\(p_{n+1}'(t)\) y\(z'(t)\) de las ecuaciones características

\ begin {eqnarray*}
p'_ {n+1} (t) &=&-h_t\\
z' (t) &=&p\ cdot\ Nabla_ph-h.
\ end {eqnarray*}

Definición. La función\(H(x,t,p)\) se llama función Hamilton, ecuación (\ ref {nonlinearham}) Ecuación de Hamilton-Jacobi y el sistema (\ ref {charhj1}), (\ ref {charhj2}) sistema canónico a H.

Existe una interesante interacción entre la ecuación Hamilton-Jacobi y el sistema canónico. Según la teoría anterior podemos construir una solución de la ecuación de Hamilton-Jacobi utilizando soluciones del sistema canónico. Por otro lado, a partir de soluciones de la ecuación de Hamilton-Jacobi se obtienen también soluciones del sistema canónico de ecuaciones diferenciales ordinarias.

Definición.
Una solución\(\phi(a;x,t)\) de la ecuación de Hamilton-Jacobi, donde\(a=(a_1,\ldots,a_n)\) es una\(n\) -tupla de parámetros reales, se denomina integral completa de la ecuación de Hamilton-Jacobi si
$$
\ det (\ phi_ {x_ia_l}) _ {i, l=1} ^n\ not=0.
\]

OBSERVACIÓN. Si\(u\) es una solución de la ecuación Hamilton-Jacobi, entonces también\(u+const.\)

Teorema 2.4 (Jacobi). Asumir

$$u=\ phi (a; x, t) +c,\ c=const.,\\ phi\ en C^2\\ mbox {en sus argumentos}, $$

es una integral completa. Entonces se obtiene resolviendo de

$$b_i=\ phi_ {a_i} (a; x, t) $$

con respecto a\(x_l=x_l(a,b,t)\), donde\(b_i\ i=1,\ldots,n\) se dan constantes reales, y luego estableciendo

$$p_k=\ phi_ {x_k} (a; x (a, b; t), t) $$

una familia de soluciones de 2n-parámetros del sistema canónico.

Comprobante. Let

$$x_l (a, b; t),\ l=1,\ ldots, n,\]

ser la solución del sistema anterior. La solución existe ya que\(\phi\) es una integral completa por suposición. Set

$$p_k (a, b; t) =\ phi_ {x_k} (a; x (a, b; t), t),\ k=1,\ ldots, n.\]

Eso lo demostraremos\(x\) y\(p\) resuelve el sistema canónico. Diferenciando\(\phi_{a_i}=b_i\) con respecto a\(t\) y la ecuación de Hamilton-Jacobi\(\phi_t+H(x,t,\nabla_x\phi)=0\) con respecto a\(a_i\), obtenemos para\(i=1,\ldots,n\)

\ begin {eqnarray*}
\ phi_ {ta_i} +\ suma_ {k=1} ^n\ phi_ {x_ka_i}\ frac {\ parcial x_k} {\ parcial t} &=&0\
\ phi_ {ta_i} +\ suma_ {k=1} ^n\ phi_ {x_ka_i} H {p_k} &==&0.
\ end {eqnarray*}
Dado que\(\phi\) es una integral completa sigue para\(k=1,\ldots,n\)

$$\ frac {\ parcial x_k} {\ parcial t} =H_ {p_k}.\]

A lo largo de una trayectoria, es decir, donde\(a,\ b\) están fijos, es\(\frac{\partial x_k}{\partial t}=x_k'(t)\). Así

$$x_k' (t) =H_ {p_k}.\]

Ahora diferenciamos\(p_i(a,b;t)\) con respecto\(t\) y\(\phi_t+H(x,t,\nabla_x\phi)=0\) respecto a\(x_i\), y obtenemos

\ begin {eqnarray*}
p_i' (t) &=&\ phi_ {x_it} +\ sum_ {k=1} ^n\ phi_ {x_ix_k} x_k' (t)\\
0&=&\ phi_ {x_it} +\ sum_ {k=1} ^n\ phi_ {x_ix_k} H_ {p_k} +H_ {x_i}\\
0&=&\ phi_ {x_it} +\ suma_ {k=1} ^n\ phi_ {x_ix_k} x_k' (t) +H_ {x_i}
\ end {eqnarray*}

De ello se deduce finalmente eso\(p_i'(t)=-H_{x_i}\).

\(\Box\)

Ejemplo 2.5.1: Problema de Kepler

El movimiento de un punto de masa en un campo central tiene lugar en un plano, digamos el\((x,y)\) plano, ver Figura 2.5.1, y satisface el sistema de ecuaciones diferenciales ordinarias de segundo orden

$$x "(t) =u_x,\ y" (t) =u_y,\]

donde

$$U (x, y) =\ frac {k^2} {\ sqrt {x^2+y^2}}.\]

Aquí asumimos que\(k^2\) es una constante positiva y que el punto de masa es atraído del origen. En el caso de que sea empujado uno tiene que sustituir\(U\) por\(-U\). Véase Landau y Lifschitz [12], Vol 1, por ejemplo, sobre la física relacionada.

Figura 2.5.1: Movimiento en un campo central

Set

$$p=x',\ q=y'\]

y

$$H=\ frac {1} {2} (p^2+q^2) -U (x, y),\]

entonces

\ begin {eqnarray*}
x' (t) &=&h_p,\ y' (t) =h_q\\
p' (t) &=&-H_x,\ q' (t) =-h_y.
\ end {eqnarray*}
La ecuación asociada de Hamilton-Jacobi es
\ begin {ecuation*}
\ phi_t+\ frac {1} 2} (\ phi_x^2+\ phi_y^2) =\ frac {k^2} {\ sqrt {x^2+y ^2}}.
\ end {ecuación*}
que está en coordenadas polares\((r,\theta)\)
\ begin {ecuación}
\ label {keplerhj}
\ phi_t+\ frac {1} {2} (\ phi_r^2+\ frac {1} {r^2}\ phi_\ theta^2) =\ frac {k^2} {r}.
\ end {ecuación}
Ahora buscaremos una integral completa de (\ ref {keplerhj}) haciendo el ansatz
\ begin {ecuación}
\ label {ansatzhj}
\ phi_t=-\ alpha=const.\\\ phi_\ theta=-\ beta=const.
\ end {ecuación}
y obtener de (\ ref {keplerhj}) que
$$
\ phi=\ pm\ int_ {r_0} ^r\\ sqrt {2\ alpha+\ frac {2k^2} {\ rho} -\ frac {\ beta^2} {\ rho^2}}\ d\ rho+c (t,\ theta).
$$
De ansatz (\ ref {ansatzhj}) sigue
$$
c (t,\ theta) =-\ alpha t-\ beta\ theta.
$$
Por lo tanto tenemos una familia de soluciones de dos parámetros
$$
\ phi=\ phi (\ alpha,\ beta;\ theta, r, t)
$$
de la ecuación Hamilton-Jacobi. Esta solución es una integral completa, ver un ejercicio.
Según el teorema del conjunto jacobi
$$
\ phi_\ alpha=-t_0,\\\ phi_\ beta=-\ theta_0.
$$
Entonces
$$
t-t_0=-\ int_ {r_0} ^r\\ frac {d\ rho} {\ sqrt {2\ alpha+\ frac {2k^2} {\ rho} -\ frac {\ beta^2} {\ rho^2}}.
$$
La función inversa\(r=r(t)\),\(r(0)=r_0\), es la\(r\) coordenada -dependiendo del tiempo\(t\), y
$$
\ theta-\ theta_0=\ beta\ int_ {r_0} ^r\\ frac {d\ rho} {\ rho^2\ sqrt {2\ alpha+\ frac {2k^2} {\ rho} -\ frac {\ beta^2} {\ rho^2}}.
$$\(\tau=\rho^{-1}\) Rendimientos de
sustitución
\ comienzan {eqnarray*}
\ theta-\ theta_0&=&-\ beta\ int_ {1/r_0} ^ {1/r}\\ frac {d\ tau} {\ sqrt {2\ alpha+2k^2\ tau-\ beta^2\ tau^2}}\\
&=&-\ arcsin\ Bigg (\ frac {\ frac {\ beta^2} {k^2}\ frac {1} {r} -1} {\ sqrt {1+ \ frac {2\ alfa\ beta^2} {k^4}}}\ Bigg)
+
\ arcsin\ Bigg (\ frac {\ frac {\ beta^2} {k^2}\ frac {1} {r_0} -1} {\ sqrt {1+\ frac {2\ alfa\ beta^2} {k^4}}}\ Bigg).
\ end {eqnarray*}
Set
$$
\ theta_1=\ theta_0+\ arcsin\ Bigg (\ frac {\ frac {\ frac {\ beta^2} {k^2}\ frac {1} {r_0} -1} {\ sqrt {1+\ frac {2\ alpha\ beta^2} {k^4}}\ Bigg)
$$
y
$$
p=\ frac {\ beta^2} {k^2},\\\ épsilon^2 =\ sqrt {1+\ frac {2\ alfa\ beta^2} {k^4}},
$$
entonces
$$
\ theta-\ theta_1=-\ arcsin\ izquierda (\ frac {\ frac {p} {r} -1} {\ epsilon^2}\ derecha).
$$
Sigue
$$
r=r (\ theta) =\ frac {p} {1-\ epsilon^2\ sin (\ theta-\ theta_1)},
$$
que es la ecuación polar de secciones cónicas. Define una elipse si\(0\le\epsilon<1\), una parábola si\(\epsilon=1\) y una hipérbola si\(\epsilon>1\), ver Figura 2.5.2 para el caso de una elipse, donde el origen del sistema de coordenadas es uno de los puntos focales de la elipse.

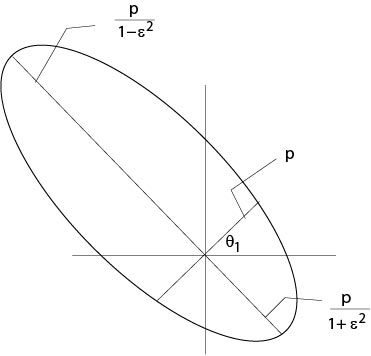
Figura 2.5.2: El caso de una elipse

Para otra aplicación del teorema jacobi véase Courant y Hilbert [4], Vol. 2, pp. 94, donde se estudian las geodésicas sobre un elipsoide.

¹ Hamilton, Guillermo Rowan, 1805—1865

² Jacobi, Carl Gustav, 1805—1851

Colaboradores y Atribuciones

• Template:ContribMiersemann
• Template:ContribMarshall