4.2.1: Caso n=3

La ecuación de Euler-Poisson-Darboux en este caso es

$$ (rM) _ {rr} =c^ {-2} (rM) _ {tt}.\]

Así$rM$ es la solución de la ecuación de onda unidimensional con datos iniciales

\ begin {ecuación}
\ label {initialn3}\ tag {4.2.1.1}
(rM) (r,0) =rF (r)\\\ (rM) _t (r,0) =rG (r).
\ end {equation}
De la fórmula d'Alembert obtenemos formalmente
\ begin {eqnarray}
\ label {meansol1}
M (r, t) &=&\ dfrac {(r+ct) F (r+ct) + (r-ct) F (r-ct)} {2r}\\ tag {4.2.1.2}
&&+\ dfrac {1} {2cr}\ int_ {r-ct} ^ {r+ct}\\ xi G (\ xi)\ d\ xi.
\ end {eqnarray}

El lado derecho de la fórmula anterior está bien definido si el dominio de dependencia$[x-ct,x+ct]$ es un subconjunto de$(0,\infty)$. Podemos extender$F$ y$G$ hacia$F_0$ y$G_0$ que se definen sobre$(-\infty,\infty)$ tal que$rF_0$ y$rG_0$ son$C^2(\mathbb{R}^1)$ -funciones de la siguiente manera.
Set

$$
F_0 (r) =\ left\ {\ begin {array} {r@ {\ qua d:\quad} l}
F (r) &r>0\\
f (x) &r=0\\
F (-r) &r<0
\ end {array}\ right. \
\]

La función$G_0(r)$ viene dada por la misma definición donde$F$ y$f$ son reemplazadas por$G$ y$g$, respectivamente.

Lema. $rF_0(r),\ rG_0(r)\in C^2(\mathbb{R}^2)$.

Prueba. De la definición de$F(r)$ y$G(r)$,$r>0$, se desprende del teorema del valor medio

$$\ lim_ {r\ a+0} F (r) =f (x),\\\\ lim_ {r\ a+0} G (r) =g (x).\]

Así$rF_0(r)$ y$rG_0(r)$ son$C(\mathbb{R}^1)$ -funciones. Estas funciones también están en$C^1(\mathbb{R}^1)$. Esto sigue desde$F_0$ y$G_0$ están en$C^1(\mathbb{R}^1)$. Tenemos, por ejemplo,

\ begin {eqnarray*}
F' (r) &=&\ dfrac {1} {\ omega_n}\ int_ {\ parcial B_1 (0)}\\ suma_ {j=1} ^n f_ {y_j} (x+r\ xi)\ xi_j\ dS_\ xi\
F' (+0) &=&\ dfrac {1}\ omega_n}\ int_ {\ parcial B_1 (0)}\\ suma_ {j=1} ^n f_ {y_j} (x)\ xi_j\ ds_\ xi\
&=&\ dfrac {1} {\ omega_n}\ suma_ {j=1} ^n f_ {y_j } (x)\ int_ {\ parcial B_1 (0)}\ n_j\ dS_\ xi\\
&=&0.
\ end {eqnarray*}

Entonces,$rF_0(r)$ y$rG_0(r)$ están en$C^2(\mathbb{R}^1)$, proveen$F''$ y$G''$ se acotan como$r\to+0$. Esta propiedad se desprende de

$$F "(r) =\ dfrac {1} {\ omega_n}\ int_ {\ parcial B_1 (0)}\\ suma_ {i, j=1} ^n f_ {y_iy_j} (x+r\ xi)\ xi_i\ xi_j\ dS_\ xi.\]

Así

$$F "(+0) =\ dfrac {1} {\ omega_n}\ suma_ {i, j=1} ^n f_ {y_iy_j} (x)\ int_ {\ parcial B_1 (0)}\ n_in_j\ dS_\ xi.\]

Eso lo recordamos$f,g\in C^2(\mathbb{R}^2)$ por suposición.

$\Box$

La solución del problema de valor inicial anterior, donde$F$ y$G$ son reemplazados por$F_0$ y$G_0$, respectivamente, es

\ begin {eqnarray*}
M_0 (r, t) &=&\ dfrac {(r+ct) F_0 (r+ct) + (r-ct) F_0 (r-ct)} {2r}\\
&&+\ dfrac {1} {2cr}\ int_ {r-ct} ^ {r+ct}\\ xi G_0 (\ xi)\ d\ xi.
\ end {eqnarray*}

Desde$F_0$ e incluso$G_0$ son funciones, tenemos

$$\ int_ {r-ct} ^ {ct-r}\\ xi G_0 (\ xi)\ d\ xi=0.\]

Así

\ begin {eqnarray}
M_0 (r, t) &=&\ dfrac {(r+ct) F_0 (r+ct) - (ct-r) F_0 (ct-r)} {2r}\ nonumber\
\ label {meansol2}\ tag {4.2.1.3}
&&+\ dfrac {1} {2cr}\ int_ {ct-r} ^ {ct+r}\\ xi G_0 (\ xi)\ d\ xi,
\ end {eqnarray}

ver Figura 4.2.1.1.

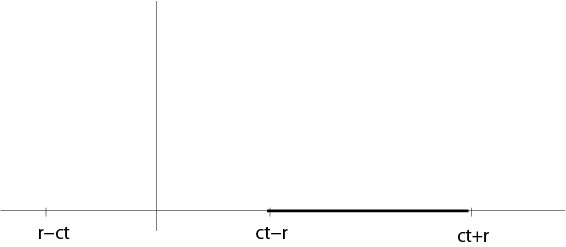
Figura 4.2.1.1: Dominio cambiado de integración

Para fijo$t>0$ y se$0<r<ct$ deduce que$M_0(r,t)$ es la solución del problema de valor inicial con datos dados inicialmente (\ ref {initialn3}) ya que$F_0(s)=F(s)$,$G_0(s)=G(s)$ si$s>0$.

Ya que para fijo$t>0$

$$u (x, t) =\ lim_ {r\ a 0} M_0 (r, t),\]

se desprende de la regla de d'Hospital que

\ begin {eqnarray*}
u (x, t) &=&CTF' (ct) +F (ct) +Tg (ct)\\
&=&\ dfrac {d} {dt}\ izquierda (tF (ct)\ derecha) +Tg (ct).
\ end {eqnarray*}

Teorema 4.2. Asumir$f\in C^3(\mathbb{R}^3)$ y$g\in C^2(\mathbb{R}^3)$ se dan. Luego existe una solución única$u\in C^2(\mathbb{R}^3\times [0,\infty))$ del problema del valor inicial (4.2.2) - (4.2.3), donde$n=3$, y la solución viene dada por la fórmula de Poisson

\ begin {eqnarray}
u (x, t) &=&\ dfrac {1} {4\ pi c^2}\ dfrac {\ parcial} {\ parcial} {\ t parcial}\ izquierda (\ dfrac {1} {t}\ int_ {\ parcial B_ {ct} (x)}\ f (y)\ ds_y\ derecha)\\ etiqueta {4.2.1.4}
&&+\ dfrac {1} {4\ pi c^2 t}\ int_ {\ parcial B_ {ct} (x)}\ g (y)\ ds_y.
\ end {eqnarray}

Prueba. Arriba hemos demostrado que una$C^2$ -solución viene dada por la fórmula de Poisson. Bajo la suposición adicional$f\in C^3$ se desprende de la fórmula de Poisson que esta fórmula define una solución que está en$C^2$, ver F. John [10], p. 129.

$\Box$

Corolario. De la fórmula de Poisson vemos que el dominio de dependencia para$u(x,t_0)$ es la intersección del cono definido por$|y-x|=c|t-t_0|$ con el hiperplano definido por$t=0$, ver Figura 4.2.1.2.

\ (n=3\).” style="width: 250px; alto: 230px;” width="250px” height="230px” src=” https://math.libretexts.org/@api/dek...pendenced3.jpg "/>

Figura 4.2.1.2: Dominio de dependencia, caso$n=3$.

Colaboradores y Atribuciones

• Template:ContribMiersemann
• Template:ContribMarshall