6.2: Nuevas Variables

Para entender la solución en todos los detalles matemáticos hacemos un cambio de variables

\[w = x + ct,\quad z = x - ct . \nonumber \]

Escribimos\(u(x,t)=\bar u(w,z)\). Nos encontramos

\[\begin{align} \dfrac{\partial}{\partial x} u & = \dfrac{\partial}{\partial w}{\bar u}\dfrac{\partial}{\partial x} w + \dfrac{\partial}{\partial z} {\bar u}\dfrac{\partial}{\partial x} z = \dfrac{\partial}{\partial w}{\bar u} + \dfrac{\partial}{\partial z} {\bar u}, \nonumber\\[4pt] \dfrac{\partial^2}{\partial x^2} u & = \dfrac{\partial^2}{\partial w^2}{\bar u}+2 \dfrac{\partial^2}{\partial w \partial z} {\bar u}+ \dfrac{\partial}{\partial z} {\bar u}, \nonumber\\[4pt] \dfrac{\partial}{\partial t} u & = \dfrac{\partial}{\partial w}{\bar u}\dfrac{\partial}{\partial t} w + \dfrac{\partial}{\partial z} {\bar u}\dfrac{\partial}{\partial t} z = c\left(\dfrac{\partial}{\partial w}{\bar u} - \dfrac{\partial}{\partial z} {\bar u}\right), \nonumber\\[4pt] \dfrac{\partial^2}{\partial t^2} u & = c^2\left(\dfrac{\partial^2}{\partial w^2}{\bar u}-2 \dfrac{\partial^2}{\partial w \partial z} {\bar u}+ \dfrac{\partial}{\partial z} {\bar u} \right)\end{align} \nonumber \]

Concluimos así que

\[\dfrac{\partial^2}{\partial x^2} u(x,t) - \frac{1}{c^2} \dfrac{\partial^2}{\partial t^2} u(x,t) = 4\dfrac{\partial^2}{\partial w \partial z} {\bar u} = 0 \nonumber \]

Una ecuación del tipo se\(\dfrac{\partial^2}{\partial w \partial z} {\bar u} = 0\) puede resolver fácilmente mediante la posterior integración con respecto a\(z\) y\(w\). Primera solución para la\(z\) dependencia,

\[\dfrac{\partial}{\partial w}{\bar u} = \Phi(w), \label{eq5} \]

donde\(\Phi\) es cualquier función de\(w\) solamente. Ahora resolver esta ecuación para la\(w\) dependencia,\[\bar u(w,z) = \int \Phi(w) dw = F(w) + G(z) \nonumber \] es decir, con\(F\) y funciones\(G\) arbitrarias.

6.2.1: Cadena Infinita

La ecuación\ ref {eq5} es bastante útil en aplicaciones prácticas. Veamos primero cómo usar esto cuando tenemos un sistema infinito (sin límites\(x\)). Supongamos que estamos tratando un problema con afecciones iniciales

\[u(x,0) = f(x),\;\;\dfrac{\partial}{\partial t} u(x,0) = g(x). \nonumber \]

Déjame asumir\(f(\pm\infty)=0\). Asumiré que esto también sirve para\(F\) y\(G\) (no tenemos que hacerlo, pero esto elimina algunas constantes arbitrarias que no juegan un papel en\(u\)). Nos encontramos

\[\begin{align} F(x)+G(x) &= f(x),\nonumber\\[4pt] c(F'(x)-G'(x)) & = g(x).\end{align} \nonumber \]

La última ecuación se puede masajear un poco para dar

\[F(x)-G(x) = \underbrace{\frac{1}{c}\int_0^x g(y) dy}_{=\Gamma(x)} + C \nonumber \]

Tenga en cuenta que\(\Gamma\) es la integral sobre\(g\). Así que siempre\(\Gamma\) será una función continua, aunque no\(g\) lo sea!

Y al final tenemos

\[\begin{align} F(x) &= \dfrac{1}{2} \left[f(x) +\Gamma(x)+C\right]\nonumber\\[4pt] G(x) &= \dfrac{1}{2} \left[f(x) -\Gamma(x)-C\right] \end{align} \nonumber \]

Supongamos que elegimos (por simplicidad tomamos\(c=1 \text{m/s}\))

\[f(x) = \begin{cases} x+1 & \text{if $-1<x<0$} \\ 1-x & \text{if $0<x<1$} \\ 0 & \text{elsewhere} \end{cases} . \nonumber \]

y\(g(x)=0\). La solución es entonces simplemente dada por\[u(x,t) = \dfrac{1}{2} \left[f(x+t)+f(x-t)\right]. \label{eq.11} \] Esto se puede resolver fácilmente gráficamente, como se muestra en la Figura \(\PageIndex{1}\).

Figura\(\PageIndex{1}\): La forma gráfica de (\ ref {eq.11}), para (de izquierda a derecha)\(t=0s\),\(t=0.5s\) y\(t=1s\). Las líneas discontinuas son\(\dfrac{1}{2} f(x+t)\) (onda móvil hacia la izquierda) y\(\dfrac{1}{2} f(x-t)\) (onda móvil hacia la derecha). La línea continua es la suma de estos dos, y por lo tanto la solución\(u\).

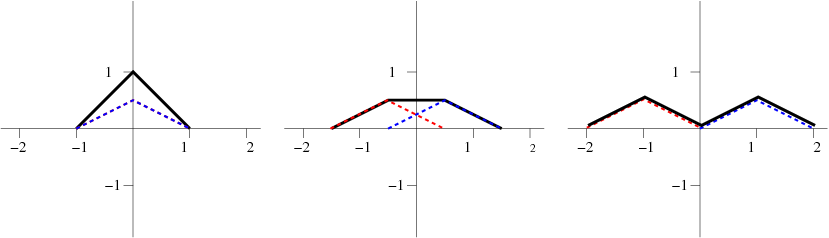
6.2.2: Cuerda Finita

El caso de una cadena finita es más complejo. Ahí nos encontramos con el problema que aunque\(f\) y solo\(g\) son conocidos por\(0<x<a\),\(x\pm ct\) pueden tomar cualquier valor de\(-\infty\) a\(\infty\). Entonces tenemos que encontrar una manera de continuar la función más allá de la longitud de la cadena. La forma de hacerlo depende del tipo de condiciones de contorno: Aquí solo consideraremos una cuerda fija en sus extremos.

\[\begin{align} u(0,t) &=u(a,t)=0,\nonumber\\[4pt] u(x,0)&=f(x)\\[4pt] \dfrac{\partial}{\partial t} u (x,0) &= g(x).\end{align} \nonumber \]

Inicialmente podemos seguir el enfoque para la cadena infinita como se esbozó arriba, y encontramos que

\[\begin{align} F(x) &= \dfrac{1}{2} \left[f(x) +\Gamma(x)+C\right], \nonumber\\[4pt] G(x) &= \dfrac{1}{2} \left[f(x) -\Gamma(x)-C\right]. \end{align} \nonumber \]

Mira la condición de contorno\(u(0,t)=0\). Demuestra que

\[\dfrac{1}{2} [f(ct)+f(-ct)]+\dfrac{1}{2} [\Gamma(ct)-\Gamma(-ct)]=0. \nonumber \]

Ahora entendemos eso\(f\) y\(\Gamma\) son funciones completamente arbitrarias —podemos escoger cualquier forma para las condiciones iniciales que queramos. Por lo tanto, la relación encontrada anteriormente solo puede sostenerse cuando ambos términos son cero

\[\begin{align} f(x)&=-f(-x),\nonumber\\[4pt] \Gamma(x)&=\Gamma(x).\label{eq:refl1}\end{align} \]

Ahora aplique la otra condición de contorno y busque

\[\begin{align} f(a+x)&=-f(a-x),\nonumber\\[4pt] \Gamma(a+x)&=\Gamma(a-x).\label{eq:refl2}\end{align} \]

Figura\(\PageIndex{2}\): A schematic representation of the reflection conditions in Equations \ref{eq:refl1} and \ref{eq:refl2}. The dashed line represents \(f\) and the dotted line \(\Gamma\).

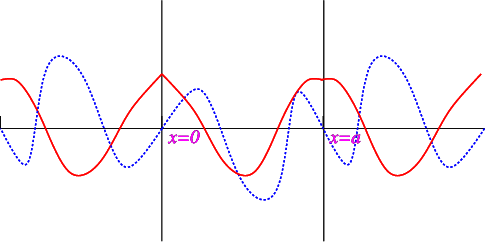
Las condiciones de reflexión para\(f\) y\(\Gamma\) son similares a las de los senos y cosenos, y como podemos ver en la Figura\(\PageIndex{2}\) ambos\(f\) y\(\Gamma\) tienen periodo\(2a\).