5.1: La transformación de Laplace
- Page ID
- 119728
Hasta este punto solo hemos explorado las transformaciones exponenciales de Fourier como un tipo de transformada integral. La transformada de Fourier es útil en dominios infinitos. Sin embargo, los estudiantes a menudo son introducidos a otra transformación integral, llamada transformada de Laplace, en su clase introductoria de ecuaciones diferenciales. Estas transformaciones se definen sobre dominios semi-infinitos y son útiles para resolver problemas de valor inicial para ecuaciones diferenciales ordinarias.
La transformación de Laplace lleva el nombre de Pierre-Simon de Laplace (1749 - 1827). Laplace hizo importantes contribuciones, especialmente a la mecánica celeste, análisis de mareas y probabilidad.
Transformar integral\([a, b]\) con respecto al núcleo integral,\(K(x, k)\).
Las transformaciones de Fourier y Laplace son ejemplos de una clase más amplia de transformaciones conocidas como transformaciones integrales. Para una función\(f(x)\) definida en un intervalo\((a, b)\), definimos la transformación integral
\[F(k)=\int_{a}^{b} K(x, k) f(x) d x\nonumber \]
donde\(K(x, k)\) es un kernel especificado de la transformada. Mirando la transformada de Fourier, vemos que el intervalo se estira sobre todo el eje real y el núcleo es de la forma,\(K(x, k)=e^{i k x}\). En el Cuadro 5.1 se muestran varios tipos de transformaciones integrales.
| Transformación de Laplace | \(F(s)=\int_{0}^{\infty} e^{-s x} f(x) d x\) |
| Transformada de Fourier | \(F(k)=\int_{-\infty}^{\infty} e^{i k x} f(x) d x\) |
| Transformada de coseno de Fourier | \(F(k)=\int_{0}^{\infty} \cos (k x) f(x) d x\) |
| Transformada sinusoidal de Fourier | \(F(k)=\int_{0}^{\infty} \sin (k x) f(x) d x\) |
| Transformación Mellin | \(F(k)=\int_{0}^{\infty} x^{k-1} f(x) d x\) |
| Transformación de Hankel | \(F(k)=\int_{0}^{\infty} x J_{n}(k x) f(x) d x\) |
Cabe señalar que estas transformaciones integrales heredan la linealidad de la integración. A saber, let\(h(x)=\alpha f(x)+\beta g(x)\), donde\(\alpha\) y\(\beta\) son constantes. Entonces,
\[\begin{aligned} H(k) &=\int_{a}^{b} K(x, k) h(x) d x \\ &=\int_{a}^{b} K(x, k)(\alpha f(x)+\beta g(x)) d x \\ &=\alpha \int_{a}^{b} K(x, k) f(x) d x+\beta \int_{a}^{b} K(x, k) g(x) d x \\ &=\alpha F(x)+\beta G(x) \end{aligned} \label{5.1} \]
Por lo tanto, hemos mostrado linealidad de las transformaciones integrales. Hemos visto la propiedad de linealidad utilizada para las transformaciones de Fourier y utilizaremos la linealidad en el estudio de las transformaciones de Laplace.
La transformación de Laplace de\(f, F=\mathcal{L}[f]\). Pasamos ahora a las transformaciones de Laplace. La transformación de Laplace de una función\(f(t)\) se define como
\[F(s)=\mathcal{L}[f](s)=\int_{0}^{\infty} f(t) e^{-s t} d t, \quad s>0 \nonumber \]
Esta es una integral inadecuada y se necesita
\[\lim _{t \rightarrow \infty} f(t) e^{-s t}=0 \nonumber \]
para garantizar la convergencia.
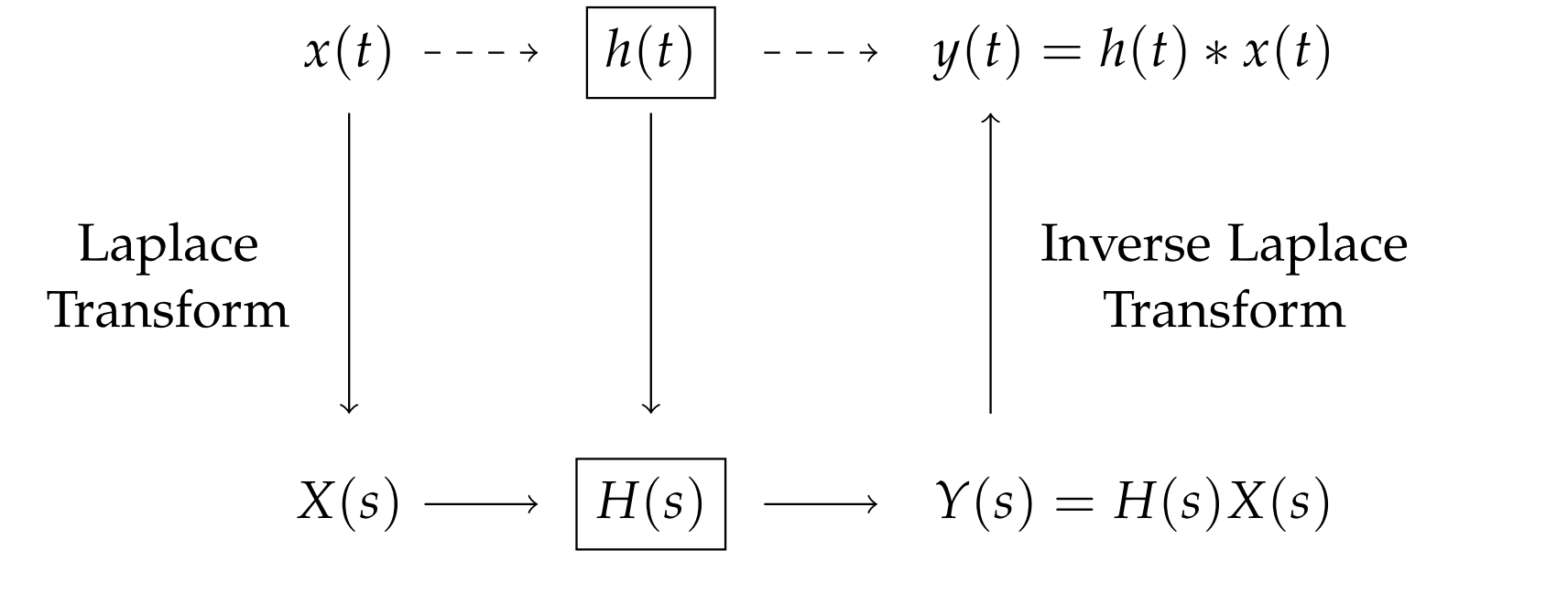
Las transformaciones de Laplace también han demostrado ser útiles en ingeniería para resolver problemas de circuitos y realizar análisis de sistemas. En la Figura\(5.1\) se muestra que\(x(t)\) se proporciona una señal como entrada a un sistema lineal, indicado por\(h(t)\). A uno le interesa la salida del sistema\(y(t)\), que viene dada por una convolución de las funciones de entrada y sistema. Al considerar las transformaciones de\(x(t)\) y\(h(t)\), la transformación de la salida se da como un producto de las transformaciones de Laplace en el dominio s. Para obtener la salida, se necesita calcular un producto de convolución para las transformaciones de Laplace similar a la operación de convolución que habíamos visto para las transformadas de Fourier anteriormente en el capítulo. Por supuesto, para que hagamos esto en la práctica, tenemos que saber calcular las transformaciones de Laplace.