6.6: Ejemplos del Método Matriz
- Page ID
- 119623
Aquí vamos a dar algunos ejemplos de sistemas típicos para los tres casos mencionados en la última sección.
\(A=\left(\begin{array}{ll}4 & 2 \\ 3 & 3\end{array}\right)\).
Valores propios: Primero determinamos los valores propios.
\[0=\left|\begin{array}{cc} 4-\lambda & 2 \\ 3 & 3-\lambda \end{array}\right| \nonumber \]
Por lo tanto,
\[ \begin{aligned} 0 &=(4-\lambda)(3-\lambda)-6 \\ 0 &=\lambda^{2}-7 \lambda+6 \\ 0 &=(\lambda-1)(\lambda-6) \end{aligned} \label{6.72} \]
Los valores propios son entonces\(\lambda=1,6\). Este es un ejemplo del Caso I.
Autovectores: A continuación determinamos los vectores propios asociados a cada uno de estos autovalores. Tenemos que resolver el sistema\(A \mathbf{v}=\lambda \mathbf{v}\) en cada caso.
Caso\(\lambda=1\).
\[\left(\begin{array}{ll} 4 & 2 \\ 3 & 3 \end{array}\right)\left(\begin{array}{l} v_{1} \\ v_{2} \end{array}\right)=\left(\begin{array}{l} v_{1} \\ v_{2} \end{array}\right) \nonumber \]
\[\left(\begin{array}{ll} 3 & 2 \\ 3 & 2 \end{array}\right)\left(\begin{array}{l} v_{1} \\ v_{2} \end{array}\right)=\left(\begin{array}{l} 0 \\ 0 \end{array}\right) \nonumber \]
Esto da\(3 v_{1}+2 v_{2}=0 .\) una solución posible produce un vector propio de
\[\left(\begin{array}{l} v_{1} \\ v_{2} \end{array}\right)=\left(\begin{array}{c} 2 \\ -3 \end{array}\right) \nonumber \]
Caso\(\lambda=6\)
\[\left(\begin{array}{cc} 4 & 2 \\ 3 & 3 \end{array}\right)\left(\begin{array}{l} v_{1} \\ v_{2} \end{array}\right)=6\left(\begin{array}{l} v_{1} \\ v_{2} \end{array}\right) \nonumber \]
\[\left(\begin{array}{cc} -2 & 2 \\ 3 & -3 \end{array}\right)\left(\begin{array}{l} v_{1} \\ v_{2} \end{array}\right)=\left(\begin{array}{l} 0 \\ 0 \end{array}\right) \nonumber \]
Para este caso tenemos que resolver\(-2 v_{1}+2 v_{2}=0\). Esto rinde
\[\left(\begin{array}{l} v_{1} \\ v_{2} \end{array}\right)=\left(\begin{array}{l} 1 \\ 1 \end{array}\right)\nonumber \]
Solución General: Ahora podemos construir la solución general.
\[ \begin{aligned} \mathbf{x}(t) &=c_{1} e^{\lambda_{1} t} \mathbf{v}_{1}+c_{2} e^{\lambda_{2} t} \mathbf{v}_{2} \\ &=c_{1} e^{t}\left(\begin{array}{c} 2 \\ -3 \end{array}\right)+c_{2} e^{6 t}\left(\begin{array}{l} 1 \\ 1 \end{array}\right) \\ &=\left(\begin{array}{c} 2 c_{1} e^{t}+c_{2} e^{6 t} \\ -3 c_{1} e^{t}+c_{2} e^{6 t} \end{array}\right) \end{aligned} \label{6.78} \]
\(A=\left(\begin{array}{rr}3 & -5 \\ 1 & -1\end{array}\right)\).
Valores propios: Una vez más, se resuelve la ecuación del valor propio.
\[0=\left|\begin{array}{cc} 3-\lambda & -5 \\ 1 & -1-\lambda \end{array}\right| \nonumber \]
Por lo tanto,
\[ \begin{aligned} 0 &=(3-\lambda)(-1-\lambda)+5 \\ 0 &=\lambda^{2}-2 \lambda+2 \\ \lambda &=\dfrac{-(-2) \pm \sqrt{4-4(1)(2)}}{2}=1 \pm i \end{aligned} \label{6.80} \]
Los valores propios son entonces\(\lambda=1+i, 1-i\). Este es un ejemplo del Caso III.
Autovectores: Para encontrar la solución general, solo necesitamos encontrar el vector propio asociado con\(1+i\).
\[ \begin{aligned} \left(\begin{array}{cc} 3 & -5 \\ 1 & -1 \end{array}\right)\left(\begin{array}{l} v_{1} \\ v_{2} \end{array}\right) &=(1+i)\left(\begin{array}{l} v_{1} \\ v_{2} \end{array}\right) \\ \left(\begin{array}{cc} 2-i & -5 \\ 1 & -2-i \end{array}\right)\left(\begin{array}{l} v_{1} \\ v_{2} \end{array}\right) &=\left(\begin{array}{l} 0 \\ 0 \end{array}\right) \end{aligned} \label{6.81} \]
Tenemos que resolver\((2-i) v_{1}-5 v_{2}=0\). Por lo tanto,
\[\left(\begin{array}{l} v_{1} \\ v_{2} \end{array}\right)=\left(\begin{array}{c} 2+i \\ 1 \end{array}\right) \nonumber \]
Solución compleja: Para obtener las dos soluciones reales linealmente independientes, necesitamos calcular las partes real e imaginaria de\(\mathbf{v} e^{\lambda t} .\)
\[e^{\lambda t}\left(\begin{array}{c} 2+i \\ 1 \end{array}\right)=e^{(1+i) t}\left(\begin{array}{c} 2+i \\ 1 \end{array}\right) \nonumber \]
\[\begin{aligned} &=e^{t}(\cos t+i \sin t)\left(\begin{array}{c} 2+i \\ 1 \end{array}\right) \\ &=e^{t}\left(\begin{array}{c} (2+i)(\cos t+i \sin t) \\ \cos t+i \sin t \end{array}\right) \\ &=e^{t}\left(\begin{array}{c} (2 \cos t-\sin t)+i(\cos t+2 \sin t) \\ \cos t+i \sin t \end{array}\right) \\ &=e^{t}\left(\begin{array}{c} 2 \cos t-\sin t \\ \cos t \end{array}\right)+i e^{t}\left(\begin{array}{c} \cos t+2 \sin t \\ \sin t \end{array}\right) \end{aligned} \nonumber \]
Solución General: Ahora podemos construir la solución general.
\[\begin{aligned} \mathbf{x}(t) &=c_{1} e^{t}\left(\begin{array}{l} 2 \cos t-\sin t \\ \cos t \end{array}\right)+c_{2} e^{t}\left(\begin{array}{c} \cos t+2 \sin t \\ \sin t \end{array}\right) \\ &=e^{t}\left(\begin{array}{c} c_{1}(2 \cos t-\sin t)+c_{2}(\cos t+2 \sin t) \\ c_{1} \cos t+c_{2} \sin t \end{array}\right) \end{aligned} \nonumber \]
Nota: Esto se puede reescribir como
\[\mathbf{x}(t)=e^{t} \cos t\left(\begin{array}{c} 2 c_{1}+c_{2} \\ c_{1} \end{array}\right)+e^{t} \sin t\left(\begin{array}{c} 2 c_{2}-c_{1} \\ c_{2} \end{array}\right) \nonumber \]
\(A=\left(\begin{array}{cc}7 & -1 \\ 9 & 1\end{array}\right)\).
Valores propios:
\[0=\left|\begin{array}{cc} 7-\lambda & -1 \\ 9 & 1-\lambda \end{array}\right| \nonumber \]
Por lo tanto,
\[ \begin{aligned} 0 &=(7-\lambda)(1-\lambda)+9 \\ 0 &=\lambda^{2}-8 \lambda+16 \\ 0 &=(\lambda-4)^{2} \end{aligned} \label{6.85} \]
Sólo hay un valor propio real,\(\lambda=4\). Este es un ejemplo del Caso II.
Autovectores: En este caso primero resolvemos para\(\mathbf{v}_{1}\) y luego obtenemos el segundo vector linealmente independiente.
\[ \begin{aligned} &\left(\begin{array}{cc} 7 & -1 \\ 9 & 1 \end{array}\right)\left(\begin{array}{l} v_{1} \\ v_{2} \end{array}\right)=4\left(\begin{array}{l} v_{1} \\ v_{2} \end{array}\right) \\ &\left(\begin{array}{cc} 3 & -1 \\ 9 & -3 \end{array}\right)\left(\begin{array}{l} v_{1} \\ v_{2} \end{array}\right)=\left(\begin{array}{l} 0 \\ 0 \end{array}\right) \end{aligned} \label{6.86} \]
Por lo tanto, tenemos
\[3 v_{1}-v_{2}=0, \quad \Rightarrow \quad\left(\begin{array}{l} v_{1} \\ v_{2} \end{array}\right)=\left(\begin{array}{l} 1 \\ 3 \end{array}\right) \nonumber \]
Segunda Solución Linealmente Independiente: Ahora tenemos que resolver\(A \mathbf{v}_{2}-\lambda \mathbf{v}_{2}=\mathbf{v}_{1}\).
\[ \begin{aligned} \left(\begin{array}{cc} 7 & -1 \\ 9 & 1 \end{array}\right)\left(\begin{array}{l} u_{1} \\ u_{2} \end{array}\right)-4\left(\begin{array}{l} u_{1} \\ u_{2} \end{array}\right) &=\left(\begin{array}{l} 1 \\ 3 \end{array}\right) \\ \left(\begin{array}{ll} 3 & -1 \\ 9 & -3 \end{array}\right)\left(\begin{array}{l} u_{1} \\ u_{2} \end{array}\right) &=\left(\begin{array}{l} 1 \\ 3 \end{array}\right) \end{aligned} \label{6.87} \]
Ampliando el producto matriz, obtenemos el sistema de ecuaciones
\[ \begin{aligned} 3 u_{1}-u_{2} &=1 \\ 9 u_{1}-3 u_{2} &=3 \end{aligned}\label{6.88} \]
La solución de este sistema es\(\left(\begin{array}{l}u_{1} \\ u_{2}\end{array}\right)=\left(\begin{array}{l}1 \\ 2\end{array}\right)\).
Solución general: Construimos la solución general como
\[ \begin{aligned} \mathbf{y}(t) &=c_{1} e^{\lambda t} \mathbf{v}_{1}+c_{2} e^{\lambda t}\left(\mathbf{v}_{2}+t \mathbf{v}_{1}\right) \\ &=c_{1} e^{4 t}\left(\begin{array}{c} 1 \\ 3 \end{array}\right)+c_{2} e^{4 t}\left[\left(\begin{array}{l} 1 \\ 2 \end{array}\right)+t\left(\begin{array}{l} 1 \\ 3 \end{array}\right)\right] \\ &=e^{4 t}\left(\begin{array}{c} c_{1}+c_{2}(1+t) \\ 3 c_{1}+c_{2}(2+3 t) \end{array}\right) \end{aligned} \label{6.89} \]
6.6.1: Sistemas Planares - Resumen
El lector debería haber notado a estas alturas que existe una conexión entre el comportamiento de las soluciones obtenidas en la Sección 6.1.3 y los valores propios encontrados a partir de las matrices de coeficientes en los ejemplos anteriores. En Tabla\(6.2\) resumimos algunos de estos casos.
| Tipo | Valores propios | Estabilidad |
|---|---|---|
| Nodo | Real\(\lambda\), mismos signos |
\(\lambda<0\), estable \(\lambda>0\), inestable |
| Sillines | Signos\(\lambda\) opuestos reales | En su mayoría inestables |
| Centro | \(\lambda\)puro imaginario | \(-\) |
| Foco/Espiral | Complejo\(\lambda, \operatorname{Re}(\lambda) \neq 0\) |
\(\operatorname{Re}(\lambda)<0\), estable \(\operatorname{Re}(\lambda)>0\), inestable |
| Nodo Degenerado | Raíces repetidas, | \(\lambda>0\), estable |
| Líneas de Equilibrios | Un valor propio cero | \(\lambda<0\), estable |
La conexión, como hemos visto, es que la ecuación característica para la ecuación diferencial de segundo orden asociada es la misma que la ecuación de valor propio de la matriz de coeficientes para el sistema lineal. Sin embargo, se debe tener un poco de cuidado en los casos en que la matriz de coeficientes no sea diagonalizable. En la Tabla\(6.3\) se encuentran tres ejemplos de sistemas con raíces repetidas. El lector debe mirar estos sistemas y mirar los puntos en común y diferencias en estos sistemas y sus soluciones. En estos casos uno tiene nodos inestables, aunque son degenerados en que solo hay un vector propio accesible.
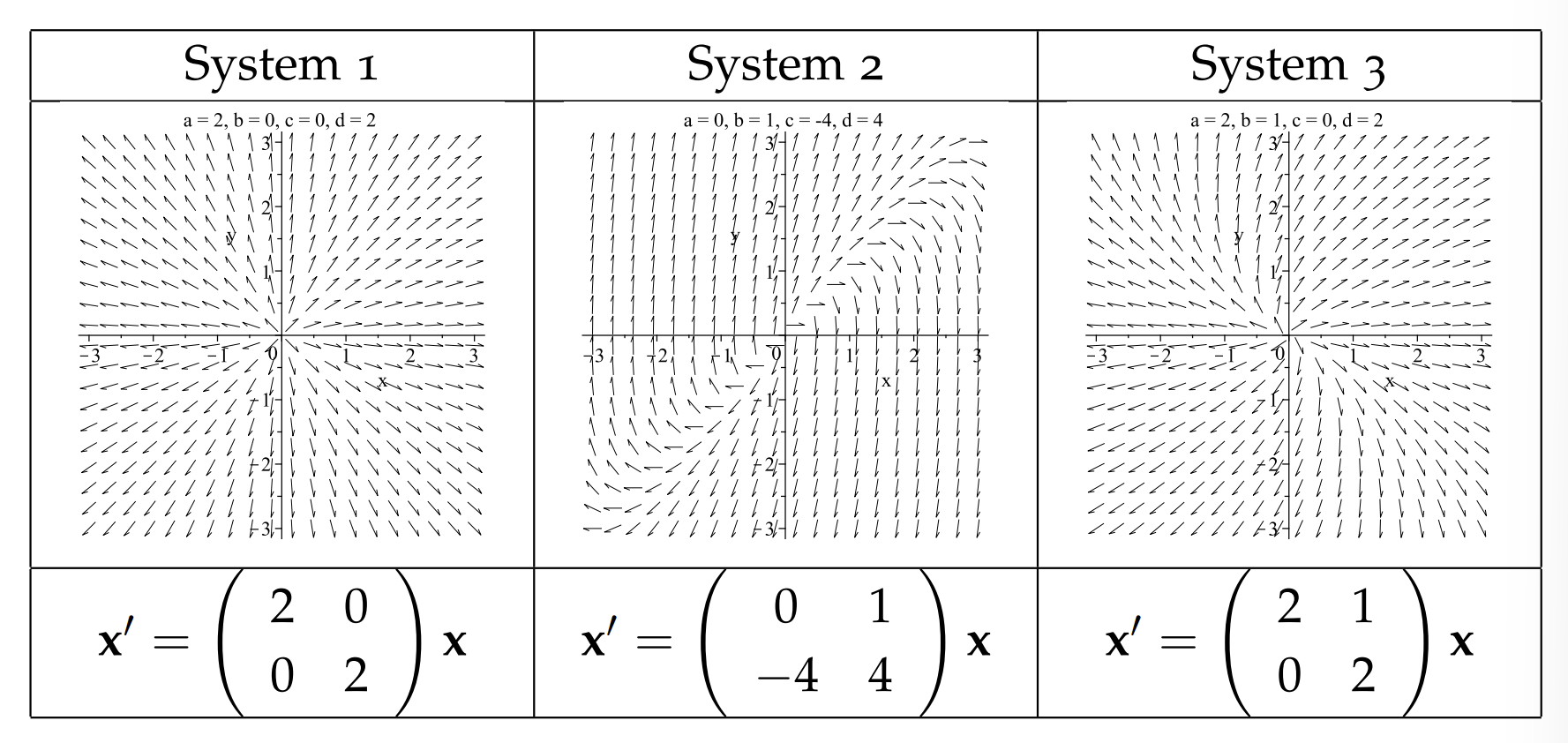
Otra forma de observar la clasificación de estas soluciones es utilizar el determinante y la traza de la matriz de coeficientes. Recordemos que el determinante y el rastro de\(A=\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)\) están dados por\(\operatorname{det} A=a d-b c\) y\(\operatorname{tr} A=a+d\)
Observamos que la ecuación general del valor propio,
\[\lambda^{2}-(a+d) \lambda+a d-b c=0 \nonumber \]
se puede escribir como
\[\lambda^{2}-(\operatorname{tr} A) \lambda+\operatorname{det} A=0 \nonumber \]
Por lo tanto, los valores propios se encuentran a partir de la fórmula cuadrática como
\[\lambda_{1,2}=\dfrac{\operatorname{tr} A \pm \sqrt{(\operatorname{tr} A)^{2}-4 \operatorname{det} A}}{2} \nonumber \]
El comportamiento de la solución depende entonces del signo de discriminante,
\[(\operatorname{tr} A)^{2}-4 \operatorname{det} A \nonumber \]
Si consideramos una trama de donde se desvanece el discriminante, entonces podríamos trazar
\[(\operatorname{tr} A)^{2}=4 \operatorname{det} A \nonumber \]
en el plano\(\operatorname{det} A \operatorname{tr} A\)). Se trata de una cura parabólica como se muestra por la línea discontinua en la Figura\(6.25\). La región dentro de la parábola tiene un discriminante negativo, lo que lleva a raíces complejas. En estos casos tenemos soluciones oscilatorias. Si\(\operatorname{tr} A=0\), entonces uno tiene centros. Si\(\operatorname{tr} A<0\), las soluciones son espirales estables; de lo contrario, son espirales inestables. Si el discriminante es positivo, entonces las raíces son reales, lo que lleva a nodos o sillas de montar en las regiones indicadas.


