2.6: Ejemplos del Método Matriz
- Page ID
- 118911
Aquí vamos a dar algunos ejemplos de sistemas típicos para los tres casos mencionados en la última sección.
\ [0=\ izquierda|\ begin {array} {cc}
4-\ lambda & 2\\
3 & 3-\ lambda
\ end {array}\ derecha|\ label {2.44}\]
Por lo tanto,
\ [\ begin {alineado}
&0 =( 4-\ lambda) (3-\ lambda) -6\\
&0=\ lambda^ {2} -7\ lambda+6\\
&0 =(\ lambda-1) (\ lambda-6)
\ end {alineado}\ etiqueta {2.45}\]
Los valores propios son entonces\(\lambda=1,6\). Este es un ejemplo del Caso I.
Autovectores: A continuación determinamos los vectores propios asociados a cada uno de estos autovalores. Tenemos que resolver el sistema\(A \mathbf{v}=\lambda \mathbf{v}\) en cada caso.
Caso\(\lambda=1\)
\ [\ begin {aligned}
&\ left (\ begin {array} {ll}
4 & 2\\
3 & 3
\ end {array}\ right)\ left (\ begin {array} {l}
v_ {1}\\
v_ {2}
\ end {array}\ right) =\ left (\ begin {array} {l}
v_ {1}\\
v_ {2}
\ end {array}\ derecha)
\ end {alineado}\ label {2.46}\]
\ [\ begin {aligned}
&\ left (\ begin {array} {ll}
3 & 2\\
3 & 2
\ end {array}\ right)\ left (\ begin {array} {l}
v_ {1}\\
v_ {2}
\ end {array}\ right) =\ left (\ begin {array} {l}
0\\
0
\ end {array}\ derecha)
\ end {alineado}\ label {2.47}\]
Esto da\(3 v_{1}+2 v_{2}=0\). Una posible solución produce un vector propio de
\ (\ left (\ begin {array} {l}
v_ {1}\\
v_ {2}
\ end {array}\ right) =\ left (\ begin {array} {c}
2\\
-3
\ end {array}\ right)\)
Caso\(\lambda=6\).
\ [\ begin {aligned}
&\ left (\ begin {array} {ll}
4 & 2\\
3 & 3
\ end {array}\ right)\ left (\ begin {array} {l}
v_ {1}\\
v_ {2}
\ end {array}\ right) =6\ left (\ begin {array} {l}
v_ {1}\\
v _ {2}
\ end {array}\ derecha)\
\ final {alineado}\ etiqueta {2.48}\]
\ [\ begin {aligned}
&\ left (\ begin {array} {cc}
-2 & 2\\
3 & -3
\ end {array}\ right)\ left (\ begin {array} {l}
v_ {1}\\
v_ {2}
\ end {array}\ right) =\ left (\ begin {array} {l}
0\\
0
\ end {array}\ derecha)
\ end {alineado}\ label {2.49}\]
Para este caso tenemos que resolver\(-2 v_{1}+2 v_{2}=0\). Esto rinde
\ (\ left (\ begin {array} {l}
v_ {1}\\
v_ {2}
\ end {array}\ right) =\ left (\ begin {array} {l}
1\\
1
\ end {array}\ right)\)
Solución General: Ahora podemos construir la solución general.
\ [\ begin {alineado}
\ mathbf {x} (t) &=c_ {1} e^ {\ lambda_ {1} t}\ mathbf {v} _ {1} +c_ {2} e^ {\ lambda_ {2} t}\ mathbf {v} _ _ {2}\
&=c_ {1} e^ {t}\ left (\ begin {array} {c}
2\\
-3
\ end {array}\ derecha) +c_ {2} e^ {6 t}\ left (\ begin {array} {l}
1 \\
1
\ end {array}\ derecha)\\
&=\ left (\ begin {array} {c}
2 c_ {1} e^ {t} +c_ {2} e^ {6 t}\\
-3 c_ {1} e^ {t} +c_ {2} e^ {6 t}
\ end {array}\ right)
\ end {alineado}\ label {2.50}\]
Valores propios: Una vez más, se resuelve la ecuación del valor propio.
\ [0=\ izquierda|\ begin {array} {cc}
3-\ lambda y -5\\
1 & -1-\ lambda
\ end {array}\ derecha|\ label {2.51}\]
Por lo tanto,
\ [\ begin {alineado}
&0 =( 3-\ lambda) (-1-\ lambda) +5\\
&0=\ lambda^ {2} -2\ lambda+2\\
&\ lambda=\ dfrac {- (-2)\ pm\ sqrt {4-4 (1) (2)}} {2} =1\ pm i
\ end {alineado}\ etiqueta {2.52}\]
Los valores propios son entonces\(\lambda=1+i, 1-i\). Este es un ejemplo del Caso III.
Autovectores: Para encontrar la solución general, solo necesitamos encontrar el vector propio asociado con\(1+i\).
\ [\ begin {alineado}
\ left (\ begin {array} {c}
3-5\\
1-1
\ end {array}\ right)\ left (\ begin {array} {l}
v_ {1}\
v_ {2}
\ end {array}\ right) & =( 1+i)\ left (\ begin {array} {l}
v_ {1}\\
v_ {2}
\ end {array}\ right)\
\ left (\ begin {array} {cc}
2-i & -5\\
1 & -2-i
\ end {array}\ right)\ left (\ begin {array} {l}
v_ {1}\\
v_ {2}
\ end {array}\ right) &=\ left (\ begin {array} {l}
0\\
0
\ end {array}\ derecha)
\ end {alineado}\ label {2.53}\]
Tenemos que resolver\((2-i) v_{1}-5 v_{2}=0\). Por lo tanto,
\ [\ left (\ begin {array} {l}
v_ {1}\\
v_ {2}
\ end {array}\ right) =\ left (\ begin {array} {c}
2+i\\
1
\ end {array}\ derecha)\ label {2.54}\]
Solución compleja: Para obtener las dos soluciones reales linealmente independientes, necesitamos calcular las partes real e imaginaria de\(v e^{\lambda t}\).
\ begin {aligned}
e^ {\ lambda t}\ left (\ begin {array} {c}
2+i\\
1
\ end {array}\ right) &=e^ {(1+i) t}\ left (\ begin {array} {c}
2+i\\
1
\ end {array}\ right)\\
&=e^ {t} (\ cos t+i\ sin t)\ left (\ comenzar { array} {c}
2+i\\
1
\ end {array}\ derecha)\\
&=e^ {t}\ left (\ begin {array} {c}
(2+i) (\ cos t+i\ sin t)\
\ cos t+i\ sin t
\ end {array}\ right)\\
&=e^ {t}\ left (\ begin {array} {c}
(2\ cos t-\ sin t) +i (\ cos t+2\ sin t)\
\ cos t+i\ sin t
\ end {array}\ derecha) +i e^ {t}\ left (\ begin {array} {c}
\ cos t+2\ sin t\\ sin t\
\ sin t
\ end {array}\ right). \\
&=e^ {t}\ left (\ begin {array} {c}
2\ cos t-\ sin t\\ cos t
\\ cos t
\ end {array}\ derecha)
\ end {alineado}
Solución General: Ahora podemos construir la solución general.
\ [\ begin {alineado}
\ mathbf {x} (t) &=c_ {1} e^ {t}\ left (\ begin {array} {l}
2\ cos t-\ sin t\\ cos t
\
\ cos t\ end {array}\ derecha) +c_ {2} e^ {t}\ left (\ begin {array} {c}
\ cos t+2\ sin t\
\ sin t
\ end {array}\ derecha)\\
&=e^ {t}\ left (\ begin {array} {c}
c_ {1} (2\ cos t-\ sin t) +c_ {2} (\ cos t+2\ sin t)\\
c_ {1}\ cos t+c_ {2}\ sin t
\ end {array}\ derecha)
\ end {alineada}\ label {2.55}\]
Nota: Esto se puede reescribir como
\ (\ mathbf {x} (t) =e^ {t}\ cos t\ left (\ begin {array} {c}
2 c_ {1} +c_ {2}\\
c_ {1}
\ end {array}\ derecha) +e^ {t}\ sin t\ left (\ begin {array} {c}
2 c_ {2} -c_ {1}\ c_ {1}\
c_ {2}
\ end {array}\ derecha)\)
Valores propios:
\ [0=\ izquierda|\ begin {array} {cc}
7-\ lambda & -1\\
9 & 1-\ lambda
\ end {array}\ derecha|\ label {2.56}\]
Por lo tanto,
\ [\ begin {alineado}
&0 =( 7-\ lambda) (1-\ lambda) +9\\
&0=\ lambda^ {2} -8\ lambda+16\\
&0 =(\ lambda-4) ^ {2}
\ end {alineado}\ etiqueta {2.57}\]
Sólo hay un valor propio real,\(\lambda=4\). Este es un ejemplo del Caso II.
Autovectores: En este caso primero resolvemos para\(\mathbf{v}_{1}\) y luego obtenemos el segundo vector linealmente independiente.
\ [\ begin {aligned}
&\ left (\ begin {array} {cc}
7 & -1\\
9 & 1
\ end {array}\ right)\ left (\ begin {array} {l}
v_ {1}\\
v_ {2}
\ end {array}\ right) =4\ left (\ begin {array} {l}
v_ {1}\\
v_ {2}
\ end {array}\ right)\\
&\ left (\ begin {array} {ll}
3 & -1\\
9 & -3
\ end {array}\ right)\ left (\ begin {array} {l}
v_ {1}\\
v_ {2}
\ end {array}\ right) =\ left (\ begin {array} {l}
0\\
0
\ end {array}\ derecha)
\ end {alineado}\ label {2.58}\]
Por lo tanto, tenemos
\ (3 v_ {1} -v_ {2} =0,\ quad\ Rightarrow\ quad\ left (\ begin {array} {l}
v_ {1}\\
v_ {2}
\ end {array}\ right) =\ left (\ begin {array} {l}
1\\
3
\ end {array}\ right)\)
Segunda solución linealmente independiente:
Ahora tenemos que resolver\(A \mathbf{v}_{2}-\lambda \mathbf{v}_{2}=\mathbf{v}_{1}\).
\ [\ begin {aligned}
\ left (\ begin {array} {cc} 7 & -1\\ 9 & 1\ end {array}\ right)\ left (\ begin {array} {l} u_ {1}\\ u_ {2}\ end {array}\ right) -4\ left (\ begin {array} {l} u_ {1}\ u_ {2}\ end {array}\ derecha) &=\ left (\ begin {array} {l} 1\\ 3\ end {array}\ right)\
\ left (\ begin {array} {ll} 3 & -1\\ 9 & -3\ end {array}\ derecha)\ left (\ begin {array} {l} u_ {1}\\ u_ {2}\ end {array}\ right) &=\ left (\ begin {array} {l} 1\\ 3\ end {array}\ derecha)
\ end {alineada}\ label {2.59}\]
Ampliando el producto matriz, obtenemos el sistema de ecuaciones
\ [\ begin {array} {r}
3 u_ {1} -u_ {2} =1\\
9 u_ {1} -3 u_ {2} =3
\ end {array}\ label {2.60}\]
La solución de este sistema es\(\left(\begin{array}{l}u_{1} \\ u_{2}\end{array}\right)=\left(\begin{array}{l}1 \\ 2\end{array}\right)\).
Solución general: Construimos la solución general como
\ [\ begin {alineado}
\ mathbf {y} (t) &=c_ {1} e^ {\ lambda t}\ mathbf {v} _ {1} +c_ {2} e^ {\ lambda t}\ izquierda (\ mathbf {v} _ {2} +t\ mathbf {v} _ _ {1}\ derecha)\\
&=c_ {1} e^ {4 t}\ left (\ begin {array} {l}
1\\
3
\ end {array}\ right) +c_ {2} e^ {4 t}\ left [\ left (\ begin {array} {l}
1\\
2
\ end {array}\ derecha) +t\ left (\ begin {array} {l}
1\\
3
\ end {array}\ derecha)\ derecha]\\
&=e^ {4 t}\ left (\ begin {array} {c}
c_ {1} +c_ {2} (1+t)\\
3 c_ {1} +c_ {2} (2+3 t)
\ end {array}\ derecha)
\ end {alineado}\ label {2.61}\]
2.6.1 Sistemas Planares - Resumen
El lector debería haber notado a estas alturas que existe una conexión entre el comportamiento de las soluciones obtenidas en la Sección 2.2 y los valores propios encontrados a partir de las matrices de coeficientes en los ejemplos anteriores. Aquí resumimos algunos de estos casos.
| Tipo | Figura | Valores propios | Estabilidad |
|---|---|---|---|
| Nodo | 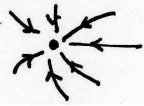 |
Real\(\lambda\), mismos signos | \(\lambda > 0\), estable |
| Sillin | 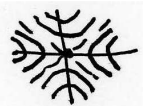 |
Signos\(\lambda\) opuestos reales | Mayormente Inestable |
| Centro |  |
\(\lambda\)puro imaginario | _____ |
|
Foco/Espiral Nodo Degenerado Línea de Equilibrios |
 |
Complejo\(\lambda\), Re (\(\lambda \neq 0\) Raíces repetidas\(\lambda > 0\), estables Un valor propio cero |
Re (\(\lambda > 0\)), estable \(\lambda > 0\), estable |
Cuadro 2.1. Listado de comportamientos típicos en sistemas planos.
La conexión, como hemos visto, es que la ecuación característica para la ecuación diferencial de segundo orden asociada es la misma que la ecuación de valor propio de la matriz de coeficientes para el sistema lineal. Sin embargo, se debe tener un poco de cuidado en los casos en que la matriz de coeficientes no sea diagonalizable. En el Cuadro 2.2 se encuentran tres ejemplos de sistemas con raíces repetidas. El lector debe mirar estos sistemas y mirar los puntos en común y diferencias en estos sistemas y sus soluciones. En estos casos uno tiene nodos inestables, aunque son degenerados en que solo hay un vector propio accesible.


