2.7: Teoría de Sistemas de Coeficiente Constante Homogéneo
- Page ID
- 118916
Existe una teoría general para resolver sistemas de coeficientes homogéneos y constantes de ecuaciones diferenciales de primer orden. Comenzamos recordando una vez más el problema específico (2.12). Obtuvimos la solución a este sistema como
\ [\ begin {reunió}
x (t) =c_ {1} e^ {t} +c_ {2} e^ {-4 t}\\
y (t) =\ dfrac {1} {3} c_ {1} e^ {t} -\ dfrac {1} {2} c_ {2} e^ {-4 t}
\ end {reunidos}\ etiqueta {2.62}\]
| Sistema 1 | Sistema 2 | Sistema 3 |
|---|---|---|
 |
 |
 |
| \ (\ mathbf {x} ^ {\ prime} =\ left (\ begin {array} {ll} 2 & 0\\ 0 & 2 \ end {array}\ derecha)\ mathbf {x}\) |
\ (\ mathbf {x} ^ {\ prime} =\ left (\ begin {array} {ll} 0 & 1\\ -4 & 4 \ end {array}\ right)\ mathbf {x}\) |
\ (\ mathbf {x} ^ {\ prime} =\ left (\ begin {array} {ll} 2 & 1\\ 0 & 2 \ end {array}\ derecha)\ mathbf {x}\) |
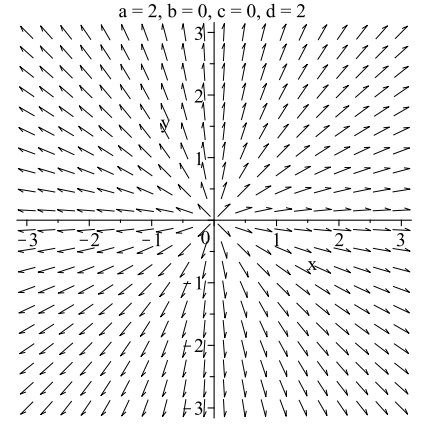
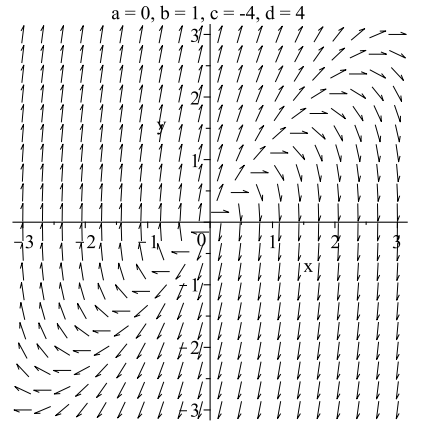
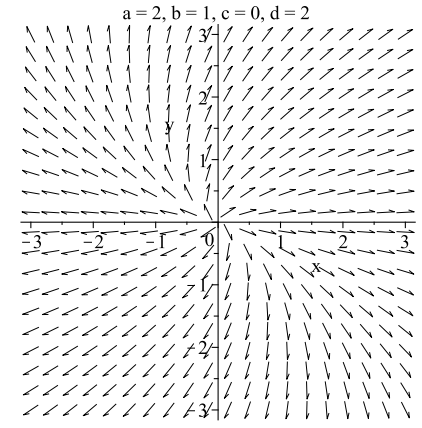
Cuadro 2.2. Tres ejemplos de sistemas con una raíz repetida de\(\lambda = 2\).
Esta vez reescribimos la solución como
\ [\ begin {alineado}
\ mathbf {x} &=\ left (\ begin {array} {c}
c_ {1} e^ {t} +c_ {2} e^ {-4 t}\
\ dfrac {1} {3} c_ {1} e^ {t} -\ dfrac {1} {2} c_ {2} e^ {t -4}
fin {array}\ derecha)\\
&=\ left (\ begin {array} {cc}
e^ {t} & e^ {-4 t}\\
\ dfrac {1} {3} e^ {t} -\ dfrac {1} {2} e^ {-4 t}
\ end {array}\ derecha)\ left (\ begin {array} {l}
c_ {1}\
c_ {2}
\ end {array}\ right)\\
&\ equiv\ Phi (t)\ mathbf {C}
\ end {alineado}\ etiqueta {2.63}\]
Así, podemos escribir la solución general como una\(2 \times 2\) matriz\(\Phi\) multiplicada por un vector constante arbitrario. La matriz\(\Phi\) consta de dos columnas que son soluciones linealmente independientes del sistema original. Esta matriz es un ejemplo de lo que vamos a definir como la Matriz Fundamental de soluciones del sistema. Entonces, determinar la Matriz Fundamental nos permitirá encontrar la solución general del sistema tras la multiplicación por una matriz constante. De hecho, veremos que también conducirá a una simple representación de la solución del problema de valor inicial para nuestro sistema. Vamos a esbozar la teoría general.
Considerar el sistema de coeficientes homogéneos y constantes de las ecuaciones diferenciales de primer orden
\ [\ begin {alineado}
\ dfrac {d x_ {1}} {d t} &=a_ {11} x_ {1} +a_ {12} x_ {2} +\ ldots+a_ {1 n} x_ {n}\
\ dfrac {d x_ {2}} {d t} &=a_ {21} x_ {1} a_ {22} x_ {2} +\ ldots+a_ {2 n} x_ {n}\\
&\ vdots\\
\ dfrac {d x_ {n}} {d t} &=a_ {n 1} x_ {1} +a_ {n 2} x_ {2} +\ ldots+a_ {n n} x_ {n}
\ final {alineado}\ etiqueta {2.64}\]
Como hemos visto, esto se puede escribir en forma de matriz\(\mathbf{x}^{\prime}=A \mathbf{x}\), donde
\ (\ mathbf {x} =\ left (\ begin {array} {c}
x_ {1}\\
x_ {2}\\
\ vdots\\
x_ {n}
\ end {array}\ derecha)\)
y
\ (A=\ left (\ begin {array} {cccc}
a_ {11} & a_ {12} &\ cdots & a_ {1 n}\\
a_ {21} & a_ {22} &\ cdots & a_ {2 n}\\ vdots &
\ vdots &\ ddots &\ vdots\\ vdots\\
a_ {n 1} & a_ {n 2} &\ cdots & a_ {n n}
\ end {array} \ derecha)\)
Ahora, considere soluciones\(m\) vectoriales de este sistema:\(\phi_{1}(t), \phi_{2}(t), \ldots \phi_{m}(t)\).
Se dice que estas soluciones son linealmente independientes en algún dominio si
\[c_{1} \phi_{1}(t)+c_{2} \phi_{2}(t)+\ldots+c_{m} \phi_{m}(t)=0 \nonumber \]
para todos\(t\) en el dominio implica eso\(c_{1}=c_{2}=\ldots=c_{m}=0\).
\(\phi_{1}(t), \phi_{2}(t), \ldots \phi_{n}(t)\)Sea un conjunto de soluciones\(n\) linealmente independientes de nuestro sistema, llamado conjunto fundamental de soluciones. Construimos una matriz a partir de estas soluciones utilizando estas soluciones como la columna de esa matriz. Definimos esta matriz como la solución matriz fundamental. Esta matriz toma la forma
\ (\ Phi=\ izquierda (\ phi_ {1}\ ldots\ phi_ {n}\ derecha) =\ izquierda (\ begin {array} {cccc}
\ phi_ {11} &\ phi_ {12} &\ cdots &\ phi_ {1 n}\
\ phi_ {21} &\ phi_ {22} &\ cdots &\ phi_ {2 n}\
\ vdots &\ vdots &\ ddots &\ vdots\\
\ phi_ {n 1} & \ phi_ {n 2} &\ cdots &\ phi_ {n n}
\ end {array}\ derecha)\)
¿A qué nos referimos con una solución “matricial”? Hemos asumido que cada uno\(\phi_{k}\) es una solución de nuestro sistema. Por lo tanto, tenemos eso\(\phi_{k}^{\prime}=A \phi_{k}\), para\(k=1, \ldots, n\). Decimos que\(\Phi\) es una solución matricial porque podemos demostrar que\(\Phi\) también satisface la formulación matricial del sistema de ecuaciones diferenciales. Podemos mostrar esto usando las propiedades de las matrices.
\ [\ begin {alineado}
\ dfrac {d} {d t}\ Phi &=\ izquierda (\ phi_ {1} ^ {\ prime}\ ldots\ phi_ {n} ^ {\ prime}\ derecha)\\
&=\ izquierda (A\ phi_ {1}\ ldots A\ phi_ {n}\ derecha)\\
&=A\ izquierda (\ phi_ {1}\ ldots\ phi_ {n}\ derecha)\\
&=A\ Phi
\ end {alineado}\ etiqueta {2. 65}\]
Dado un conjunto de soluciones vectoriales del sistema, ¿cuándo son linealmente independientes? Consideramos una solución matricial\(\Omega(t)\) del sistema en el que tenemos soluciones\(n\) vectoriales. Entonces, definimos el Wronskian\(\Omega(t)\) de ser
\[W=\operatorname{det} \Omega(t) \nonumber \]
Si\(W(t) \neq 0\), entonces\(\Omega(t)\) es una solución matriz fundamental.
Antes de continuar, enumeramos las soluciones de matriz fundamental para el conjunto de ejemplos en la última sección. (Consulte las soluciones de esos ejemplos.) Además, tenga en cuenta que las soluciones de matriz fundamental no son únicas ya que se puede multiplicar cualquier columna por una constante distinta de cero y aún así tener una solución de matriz fundamental.
\ (\ Phi (t) =\ left (\ begin {array} {cc}
2 e^ {t} & e^ {6 t}\\
-3 e^ {t} & e^ {6 t}
\ end {array}\ derecha)\)
Debemos señalar en este caso que el Wronskian se encuentra como
\ [\ begin {aligned}
W &=\ nombreoperador {det}\ Phi (t)\\
&=\ izquierda|\ begin {array} {cc}
2 e^ {t} & e^ {6 t}\\
-3 e^ {t} & e^ {6 t}
\ end {array}\ derecha|\\
&=5 e^ {7 t}\ neq 0
\ end {alineado}\ label {2.66}\]
\ (\ Phi (t) =\ left (\ begin {array} {cc}
e^ {t} (2\ cos t-\ sin t) & e^ {t} (\ cos t+2\ sin t)\\
e^ {t}\ cos t & e^ {t}\ sin t
\ end {array}\ derecha)\)
\ (\ Phi (t) =\ left (\ begin {array} {cc}
e^ {4 t} & e^ {4 t} (1+t)\\
3 e^ {4 t} & e^ {4 t} (2+3 t)
\ end {array}\ right)\)
Hasta el momento sólo hemos determinado la solución general. Esto se realiza mediante los siguientes pasos:
- Resolver el problema del valor propio\((A-\lambda I) \mathbf{v}=0\).
- Construir soluciones de vectores a partir de\(\mathbf{v} e^{\lambda t}\). El método depende si uno tiene valores propios conjugados reales o complejos.
- Formar la matriz de solución fundamental\(\Phi(t)\) a partir de la solución vector.
- La solución general viene dada por\(\mathbf{x}(t)=\Phi(t) \mathbf{C}\) para\(\mathbf{C}\) un vector constante arbitrario.
Ahora estamos listos para resolver el problema de valor inicial:
\[x' = Ax, \quad x(t_0) = x_0. \nonumber \]
Comenzando con la solución general, tenemos que
\[\mathbf{x}_{0}=\mathbf{x}\left(t_{0}\right)=\Phi\left(t_{0}\right) \mathbf{C} \nonumber \]
Como de costumbre, necesitamos resolver para los\(c_{k}\) 's. usando métodos matriciales, esto ahora es fácil. Como el Wronskian no es cero, entonces podemos invertir\(\Phi\) a cualquier valor de\(t\).
Entonces, tenemos
\[\mathbf{C}=\Phi^{-1}\left(t_{0}\right) \mathbf{x}_{0} \nonumber \]
\(\mathbf{C}\)Volviendo a la solución general, obtenemos la solución al problema de valor inicial:
\[\mathbf{x}(t)=\Phi(t) \Phi^{-1}\left(t_{0}\right) \mathbf{x}_{0} \nonumber \]
Puede verificar fácilmente que esta es una solución del sistema y satisface la condición inicial en\(t=t_{0}\).
La combinación matricial\(\Phi(t) \Phi^{-1}\left(t_{0}\right)\) es útil. Entonces, definiremos el producto resultante como la solución matriz principal, denotándolo por
\[\Psi(t)=\Phi(t) \Phi^{-1}\left(t_{0}\right) \nonumber \]
Así, la solución del problema de valor inicial es\(\mathbf{x}(t)=\Psi(t) \mathbf{x}_{0}\). Además, observamos que\(\Psi(t)\) es una solución al problema del valor inicial de la matriz
\(\mathbf{x}^{\prime}=A \mathbf{x}, \quad \mathbf{x}\left(t_{0}\right)=I\),
donde\(I\) está la matriz\(n \times n\) de identidad.
En resumen, la solución matricial de
\[\dfrac{dx}{dt} = Ax, \quad x(t_0) = x_0 \nonumber \]
está dado por
\[\mathbf{x}(t)=\Psi(t) \mathbf{x}_{0}=\Phi(t) \Phi^{-1}\left(t_{0}\right) \mathbf{x}_{0} \nonumber \]
donde\(\Phi(t)\) está la solución de matriz fundamental y\(\Psi(t)\) es la solución matriz principal.
\ [\ begin {aligned}
&x^ {\ prime} =5 x+3 y\\
&y^ {\ prime} =-6 x-4 y
\ end {alineado}\ label {2.67}\]
satisfactorias\(x(0)=1, y(0)=2\). Encuentra la solución de este problema.
Primero observamos que la matriz de coeficientes es
\ (A=\ left (\ begin {array} {cc}
5 & 3\\
-6 & -4
\ end {array}\ right)\)
La ecuación del valor propio se encuentra fácilmente a partir de
\ [\ begin {alineado}
0 &=- (5-\ lambda) (4+\ lambda) +18\\
&=\ lambda^ {2} -\ lambda-2\\
& =(\ lambda-2) (\ lambda+1)
\ final {alineado}\ etiqueta {2.68}\]
Entonces, los valores propios son\(\lambda=-1,2\). Se encuentra que los vectores propios correspondientes son
\ (\ mathbf {v} _ {1} =\ left (\ begin {array} {c}
1\\
-2
\ end {array}\ right),\ quad\ mathbf {v} _ {2} =\ left (\ begin {array} {c}
1\\
-1
\ end {array}\ right)\)
Ahora construimos la solución matriz fundamental. Las columnas se obtienen usando los vectores propios y los exponenciales,\(e^{\lambda t}\):
\ (\ phi_ {1} (t) =\ left (\ begin {array} {c}
1\\
-2
\ end {array}\ right) e^ {-t},\ quad\ phi_ {1} (t) =\ left (\ begin {array} {c}
1\
-1
\ end {array}\ right) e^ {2 t}\)
Entonces, la solución matriz fundamental es
\ (\ Phi (t) =\ left (\ begin {array} {cc}
e^ {-t} & e^ {2 t}\\
-2 e^ {-t} & -e^ {2 t}
\ end {array}\ right)\)
La solución general a nuestro problema es entonces
\ (\ mathbf {x} (t) =\ left (\ begin {array} {cc}
e^ {-t} & e^ {2 t}\\
-2 e^ {-t} & -e^ {2 t}
\ end {array}\ derecha)\ mathbf {C}\)
for\(\mathbf{C}\) es un vector constante arbitrario.
Para encontrar la solución particular del problema del valor inicial, necesitamos la solución de matriz principal. Primero evaluamos\(\Phi(0)\), luego lo invertimos:
\ (\ Phi (0) =\ left (\ begin {array} {cc}
1 & 1\\
-2 & -1
\ end {array}\ right)\ quad\ Rightarrow\ quad\ Phi^ {-1} (0) =\ left (\ begin {array} {cc}
-1 & -1\
2 & 1
\ end {array}\ right)\)
La solución particular es entonces
\ [\ begin {aligned}
\ mathbf {x} (t) &=\ left (\ begin {array} {cc}
e^ {-t} & e^ {2 t}\\
-2 e^ {-t} & -e^ {2 t}
\ end {array}\ derecha)\ left (\ begin {array} {cc}
-1 y -1\\
2 & 1
\ end {array}\ derecha)\ left (\ begin { array} {l}
1\\
2
\ end {array}\ derecha)\\
&=\ left (\ begin {array} {cc}
e^ {-t} & e^ {2 t}\\
-2 e^ {-t} & -e^ {2 t}
\ end {array}\ right)\ left (\ begin {array} {c}
-3\
4
\ end {array}\ derecha)\\
&=\ left (\ begin {array} {c}
-3 e^ {-t} +4 e^ {2 t}\\
6 e^ {-t} -4 e^ {2 t}
\ end {array}\ derecha)
\ end {alineado}\ label {2.69}\]
Así,\(x(t)=-3 e^{-t}+4 e^{2 t}\) y\(y(t)=6 e^{-t}-4 e^{2 t}\).


