2.9: Aplicaciones
- Page ID
- 118906
En esta sección describiremos varias aplicaciones que conducen a sistemas de ecuaciones diferenciales. De acuerdo con la práctica común en áreas como la física, denotaremos diferenciación con respecto al tiempo como
\[\dot{x}=\dfrac{d x}{d t} \nonumber \]
Analizaremos principalmente modelos lineales y posteriormente modificaremos algunos de estos modelos para incluir términos no lineales.
2.9.1 Sistemas de Muelle-Masa
Hay muchos problemas en la física que resultan en sistemas de ecuaciones. Esto se debe a que la ley más básica de la física la da la Segunda Ley de Newton, que establece que si un cuerpo experimenta una fuerza neta, se acelerará. En particular, la fuerza neta es proporcional a la aceleración con una constante de proporcionalidad llamada masa,\(m\). Esto se resume como
\[\sum \mathbf{F}=m \mathbf{a} \nonumber \]
Ya que\(\mathbf{a}=\ddot{\mathbf{x}}\), la Segunda Ley de Newton es matemáticamente un sistema de ecuaciones diferenciales de segundo orden para problemas tridimensionales, o una ecuación diferencial de segundo orden para problemas unidimensionales. Si hay varias masas, entonces, naturalmente, terminaríamos con sistemas sin importar cuántas dimensiones se involucren.
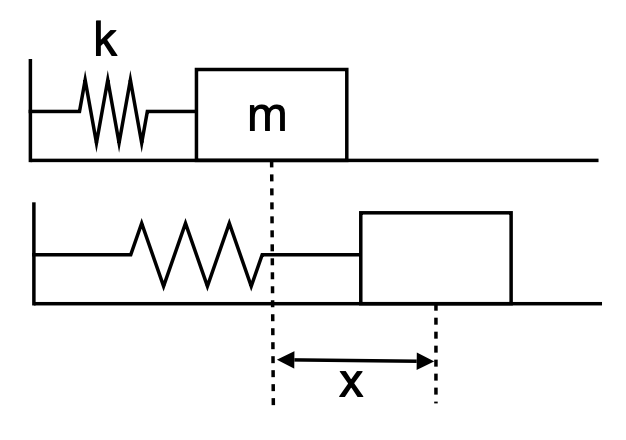
Un problema estándar que se encuentra en un primer curso en ecuaciones diferenciales es el de un solo bloque en un resorte como se muestra en la Figura 2.18. La fuerza neta en este caso es la fuerza restauradora de la primavera dada por la Ley de Hooke,
\(F_{s}=-k x\),
donde\(k>0\) esta la constante primaveral. Aquí\(x\) está el alargamiento del resorte, o el desplazamiento del bloque desde el equilibrio. Cuando\(x\) es positivo, la fuerza del resorte es negativa y cuando\(x\) es negativa la fuerza del resorte es positiva. Hemos representado un sistema horizontal sentado sobre una superficie sin fricción.
Se puede proporcionar un modelo similar para muelles orientados verticalmente. Coloca el bloque sobre un muelle que cuelga verticalmente. Se trata de equilibrio, estirando la primavera por\(\ell_{0}\). La Segunda Ley de Newton da
\[-m g+k \ell_{0}=0 \nonumber \]
Ahora, tirando más de la masa\(x_{0}\), y liberándola, la masa comienza a oscilar. Dejando\(x\) ser el desplazamiento del nuevo equilibrio, da ahora la Segunda Ley de Newton\(m \ddot{x}=-m g+k\left(\ell_{0}-x\right)=-k x\).
En ambos ejemplos (una masa oscilante horizontal o véticamente) la Segunda Ley del movimiento de Newton se reulta en la ecuación diferencial
\[m \ddot{x}+k x=0 \label{2.79} \]
Esta es la ecuación para el movimiento armónico simple que ya hemos encontrado en el Capítulo 1.
Esta ecuación de segundo orden puede escribirse como un sistema de dos ecuaciones de primer orden.
\ [\ begin {aligned}
&x^ {\ prime} =y\\
&y^ {\ prime} =-\ dfrac {k} {m} x.
\ end {alineado}\ etiqueta {2.80}\]
La matriz de coeficientes para este sistema es
\ (A=\ left (\ begin {array} {cc}
0 & 1\\
-\ omega^ {2} & 0
\ end {array}\ right)\),
donde\(\omega^{2}=\dfrac{k}{m}\). Los valores propios de este sistema son\(\lambda=\pm i \omega\) y las soluciones son simples senos y cosenos,
\ [\ begin {alineado}
x (t) &=c_ {1}\ cos\ omega t+c_ {2}\ sin\ omega t\\
y (t) &=\ omega\ izquierda (-c_ {1}\ sin\ omega t+c_ {2}\ cos\ omega t\ derecha)
\ final {alineado}\ etiqueta {2.81}\]
Observamos además que\(\omega\) se llama la frecuencia angular de oscilación y se da en\(\mathrm{rad} / \mathrm{s}\). La frecuencia de oscilación es
\[f=\dfrac{\omega}{2 \pi} \nonumber \]
Por lo general, tiene unidades de\(\mathrm{s}^{-1}, \mathrm{cps}\), o\(\mathrm{Hz}\). El inverso multiplicativo tiene unidades de tiempo y se llama el período,
\[T=\dfrac{1}{f} \nonumber \]
Así, el período de oscilación para una masa\(m\) en un resorte con constante de resorte\(k\) viene dado por
\[T=2 \pi \sqrt{\dfrac{m}{k}} \label{2.82} \]
Por supuesto, no necesitábamos convertir el último problema en un sistema. De hecho, habíamos visto esta ecuación en el Capítulo 1. Sin embargo, cuando se considera
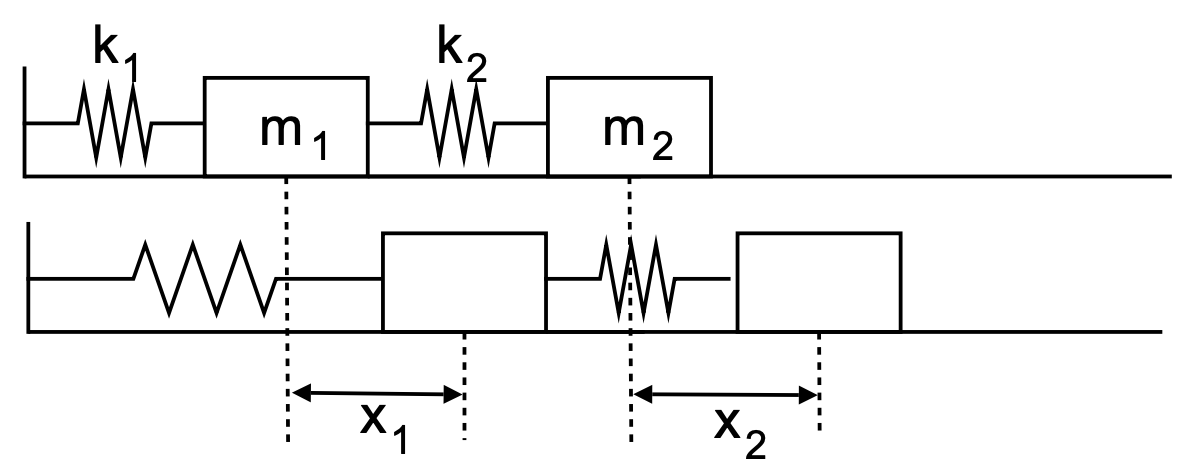
sistemas de masa-resorte más complicados, los sistemas de ecuaciones diferenciales ocurren naturalmente. Considere dos bloques unidos con dos resortes como se muestra en la Figura 2.19. En este caso aplicamos la segunda ley de Newton para cada bloque.
Primero, considere las fuerzas que actúan sobre el primer bloque. El primer resorte se estira por\(x_{1}\). Esto da una fuerza de\(F_{1}=-k_{1} x_{1}\). El segundo resorte también puede ejercer una fuerza sobre el bloque dependiendo de si se estira, o no. Si ambos bloques se desplazan en la misma cantidad, entonces el resorte no se desplaza. Entonces, la cantidad en la que se desplaza el resorte depende de los desplazamientos relativos de las dos masas. Esto resulta en una segunda fuerza de\(F_{2}=k_{2}\left(x_{2}-x_{1}\right)\).
Solo hay un resorte conectado a la masa dos. Nuevamente la fuerza depende del desplazamiento relativo de las masas. Simplemente se dirige de manera opuesta a la fuerza que se siente a partir de esta primavera.
Combinando estas fuerzas y usando la Segunda Ley de Newton para ambas masas, tenemos el sistema de ecuaciones diferenciales de segundo orden
\ [\ begin {alineado}
&m_ {1}\ ddot {x} _ {1} =-k_ {1} x_ {1} +k_ {2}\ izquierda (x_ {2} -x_ {1}\ derecha)\\
&m_ {2}\ ddot {x} _ {2} =-k_ {2}\ izquierda (x_ {2} -x_ {1}\ derecha).
\ end {alineado}\ etiqueta {2.83}\]
Se puede reescribir este sistema de dos ecuaciones de segundo orden como un sistema de cuatro ecuaciones de primer orden. Esto se hace introduciendo dos nuevas variables\(x_{3}=\dot{x}_{1}\) y\(x_{4}=\dot{x}_{2}\). Tenga en cuenta que estas físicamente son las velocidades de los dos bloques.
El sistema resultante de ecuaciones de primer orden se da como
\ [\ begin {alineado}
&\ punto {x} _ {1} =x_ {3}\\
&\ punto {x} _ {2} =x_ {4}\\
&\ punto {x} _ {3} =-\ dfrac {k_ {1}} {m_ {1}} x_ {1} +\ dfrac {k_ {2}} {m_ {m_ {1}}\ izquierda (x_ {2} -x_ {1}\ derecha)\\
&\ punto {x} _ {4} =-\ dfrac {k_ {2}} {m_ {2}}\ izquierda (x_ {2} -x_ {1}\ derecha)
\ end {alineado} \ label {2.84}\]
Podemos escribir nuestro nuevo sistema en forma de matriz como
\ [\ left (\ begin {array} {l}
\ punto {x} _ {1}\
\ punto {x} _ {2}\
\ punto {x} _ {3}\
\ punto {x} _ {4} _ {4}
\ end {array}\ derecha) =\ left (\ begin {array} {cccc}
0 & 0 & 1 & 0 & 0 & 1\
-\ dfrac {k
_ {1} +k_ {2}} {m_ {1}} &\ dfrac {k_ {2}} {m_ {1}} & 0 & 0\
\ dfrac {k_ {2}} {m_ {2}} & -\ dfrac {k_ {2}} {m_ {2}} & 0 & 0
\ end {array}\ derecha)\ izquierda (\ begin {array} {l}
x_ {1}\\
x_ {2}\\
x_ {3}\\
x_ {4}
\ end {array}\ derecha)\ label {2.85}\]
2.9.2 Circuitos eléctricos
Otro problema que a menudo se encuentra en una clase de física de primer año es el de un circuito en serie LRC. Este circuito se representa en la Figura 2.20. La resistencia es un elemento de circuito que satisface la Ley de Ohm. El condensador es un dispositivo que almacena energía eléctrica y un inductor, o bobina, almacena energía magnética.
La física para este problema proviene de las Reglas para circuitos de Kirchoff. Como solo hay un bucle, solo necesitaremos la Regla Loop de Kirchoff. A saber, la suma de las caídas en el potencial eléctrico se establece igual a las subidas en el potencial eléctrico. Las caídas potenciales a través de cada elemento del circuito están dadas por
- Resistencia:\(V_{R}=I R\).
- Capacitor:\(V_{C}=\dfrac{q}{C}\).
- Inductor:\(V_{L}=L \dfrac{d I}{d t}\).
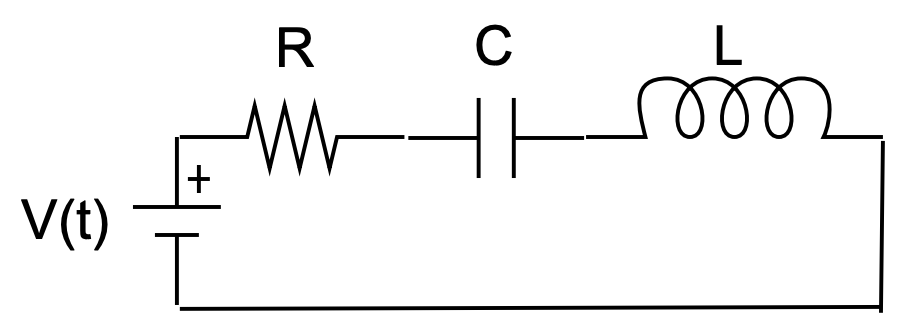
Sumando estas caídas de potencial y ajustando la suma igual al voltaje suministrado por la fuente de voltaje\(V (t)\),, obtenemos
\[I R+\dfrac{q}{C}+L \dfrac{d I}{d t}=V(t) \nonumber \]
Además, recordamos que la corriente se define como\(I=\dfrac{d q}{d t}\). donde\(q\) esta la carga en el circuito. Ya que ambos\(q\) y\(I\) son desconocidos, podemos sustituir la corriente por su expresión en términos de la carga para obtener
\[L \ddot{q}+R \dot{q}+\dfrac{1}{C} q=V(t) \label{2.86} \]
Esta es una ecuación diferencial de segundo orden para\(q(t)\). Se puede establecer un sistema de ecuaciones y proceder a resolverlas. Sin embargo, esta es una ecuación diferencial de coeficiente constante y también se puede resolver utilizando los métodos del Capítulo 1.
En los siguientes ejemplos veremos casos especiales que surgen para la ecuación del circuito LRC en serie. Estos incluyen\(RC\) circuitos, solucionables por métodos de primer orden y\(LC\) circuitos, que conducen a un comportamiento oscilatorio.
Primero consideramos el caso de un circuito RC en el que no hay inductor.
Además, consideraremos qué sucede cuando se carga un condensador con una batería de CC\(\left(V(t)=V_{0}\right)\) y cuando se descarga un condensador cargado\((V(t)=0)\).
Para cargar un condensador, tenemos el problema de valor inicial
\[R \dfrac{d q}{d t}+\dfrac{q}{C}=V_{0}, \quad q(0)=0 \label{2.87} \]
Esta ecuación es un ejemplo de una ecuación lineal de primer orden para\(q(t)\). Sin embargo, también podemos reescribir esta ecuación y resolverla como una ecuación separable, ya que\(V_{0}\) es una constante. Haremos lo primero sólo como otro ejemplo de encontrar el factor integrador.
Primero escribimos la ecuación en forma estándar:
\[\dfrac{d q}{d t}+\dfrac{q}{R C}=\dfrac{V_{0}}{R} \label{2.88} \]
El factor integrador es entonces
\[\mu(t)=e^{\int \dfrac{d t}{R C}}=e^{t / R C} \nonumber \]
Por lo tanto,
\[\dfrac{d}{d t}\left(q e^{t / R C}\right)=\dfrac{V_{0}}{R} e^{t / R C} \label{2.89} \]
Integrando, tenemos
\[q e^{t / R C}=\dfrac{V_{0}}{R} \int e^{t / R C} d t=C V_{0} e^{t / R C}+K \label{2.90} \]
Tenga en cuenta que introdujimos la constante de integración,\(K\). Ahora divide lo exponencial para obtener la solución general:
\[q=C V_{0}+K e^{-t / R C} \label{2.91} \]
(Si hubiéramos olvidado el\(K\), no habríamos conseguido una solución correcta para la ecuación diferencial.)
A continuación, utilizamos la condición inicial para obtener nuestra solución particular. A saber, el ajuste\(t = 0\), tenemos que
\[0 = q(0) = CV_0 + K. \nonumber \]
Entonces,\(K = -CV_0\). Insertando esto en nuestra solución, tenemos
\[q(t) = CV_0(1 - e^{-t/RC}) \label{2.92} \]
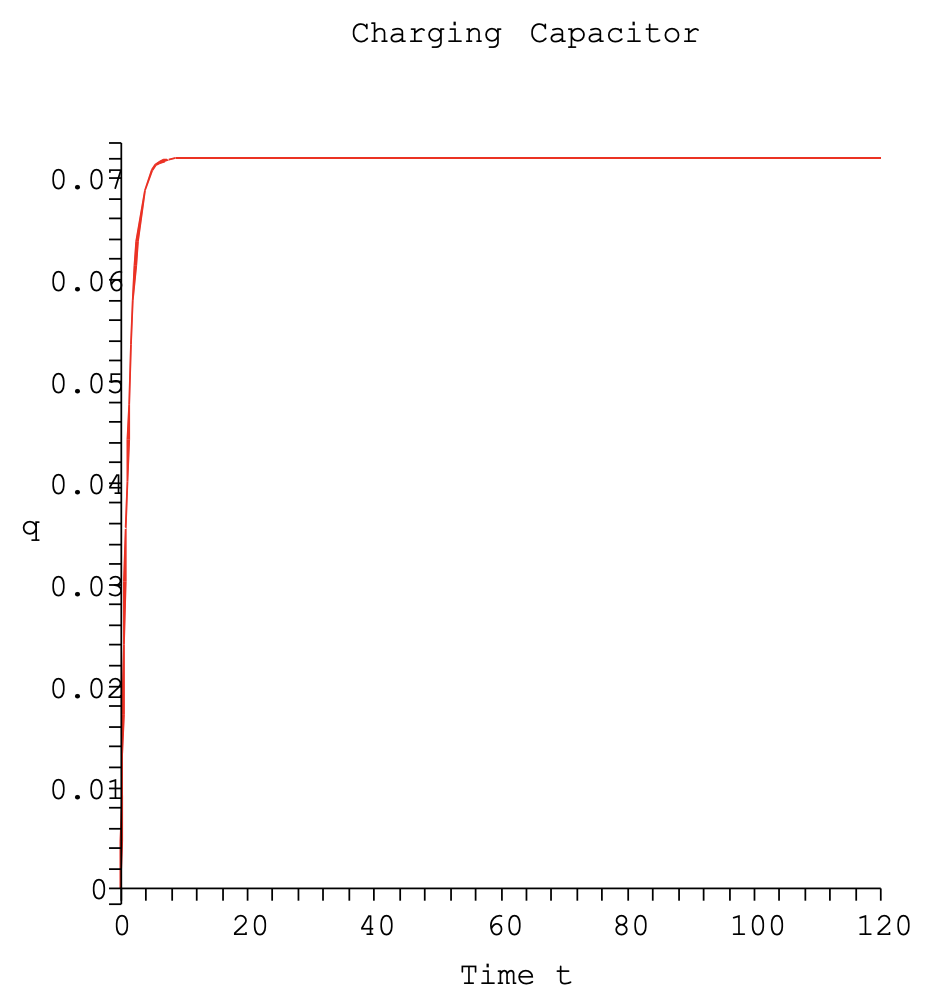
Ahora podemos estudiar el comportamiento de esta solución. Para grandes tiempos el segundo término va a cero. Así, el condensador se carga, asintóticamente, hasta el valor final de\(q_0 = CV_0\). Esto es lo que esperamos, porque la corriente ya no fluye\(R\) y esto solo da la relación entre la diferencia de potencial a través de las placas del condensador cuando\(q_0\) se establece una carga de en las placas.
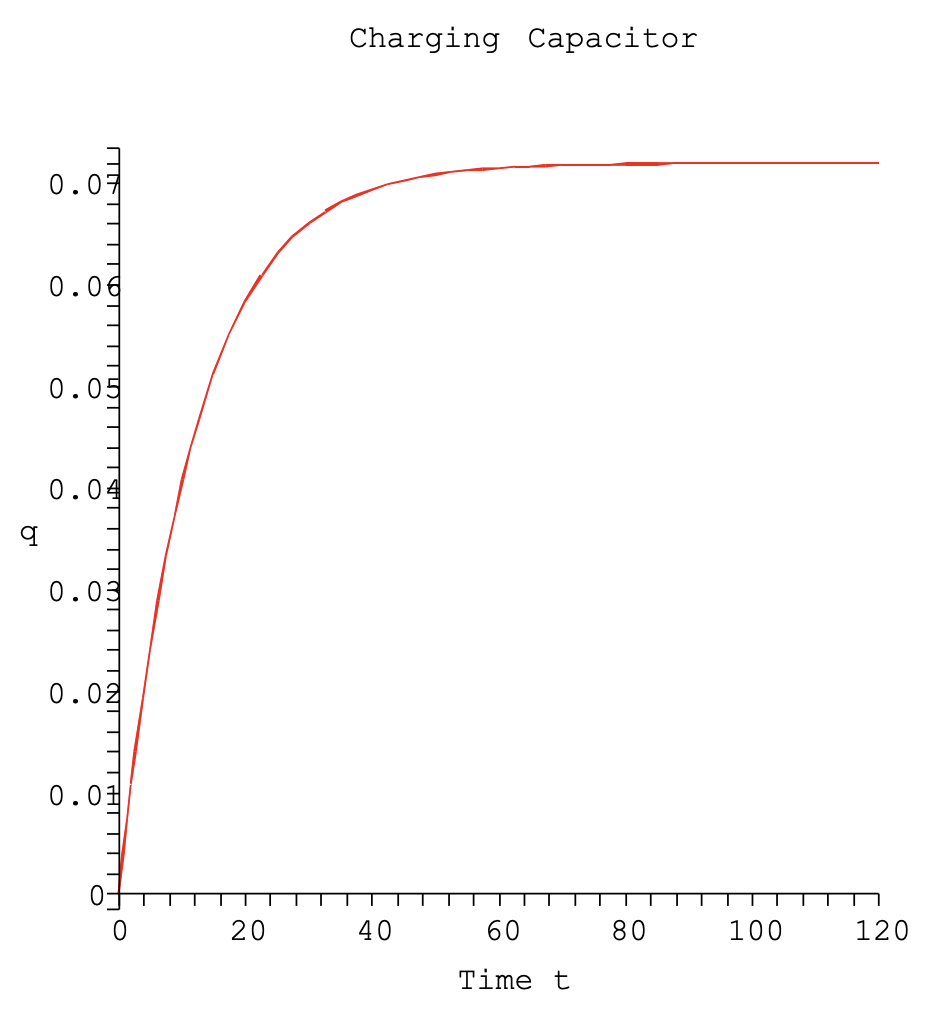
Pongamos algunos valores para los parámetros. Dejamos\(R=2.00 \mathrm{k} \Omega, C=6.00\)\(\mathrm{mF}\), y\(V_{0}=12 \mathrm{~V}\). Una gráfica de la solución se da en la Figura 2.21. Vemos que la carga se acumula hasta el valor de\(C V_{0}=72 \mathrm{mC}\). Si utilizamos una resistencia menor,\(R=200 \Omega\), vemos en la Figura 2.22 que el condensador se carga al mismo valor, pero mucho más rápido.
La velocidad a la que un condensador carga, o descarga, se rige por la constante de tiempo,\(\tau=R C\). Este es el factor constante en lo exponencial. Cuanto más grande es, más lento decae el término exponencial. Si nos fijamos\(t=\tau\), nos encontramos con que
\[q(\tau)=C V_{0}\left(1-e^{-1}\right)=(1-0.3678794412 \ldots) q_{0} \approx 0.63 q_{0} \nonumber \]
Así, en el momento\(t = \tau\), el condensador casi se ha cargado a dos tercios de su valor final. Para el primer conjunto de parámetros,\(\tau = 12s\). Para el segundo set,\(\tau = 1.2s\).
Ahora, supongamos que el condensador está cargado de carga\(\pm q_{0}\) en sus placas. Si desconectamos la batería y volvemos a conectar los cables para completar el circuito, la carga luego se moverá fuera de las placas, descargando el condensador. La forma relevante de nuestro problema de valor inicial se convierte
\[R \dfrac{d q}{d t}+\dfrac{q}{C}=0, \quad q(0)=q_{0} \label{2.93} \]
Esta ecuación es más sencilla de resolver. Reordenando, tenemos
\[\dfrac{d q}{d t}=-\dfrac{q}{R C} \label{2.94} \]
Se trata de un simple problema de decaimiento exponencial, que puedes resolver usando la separación de variables. No obstante, a estas alturas ya deberías saber cómo anotar de inmediato la solución a tales problemas de la forma\(y^{\prime}=k y\). La solución es
\[q(t)=q_{0} e^{-t / \tau}, \quad \tau=R C \nonumber \]
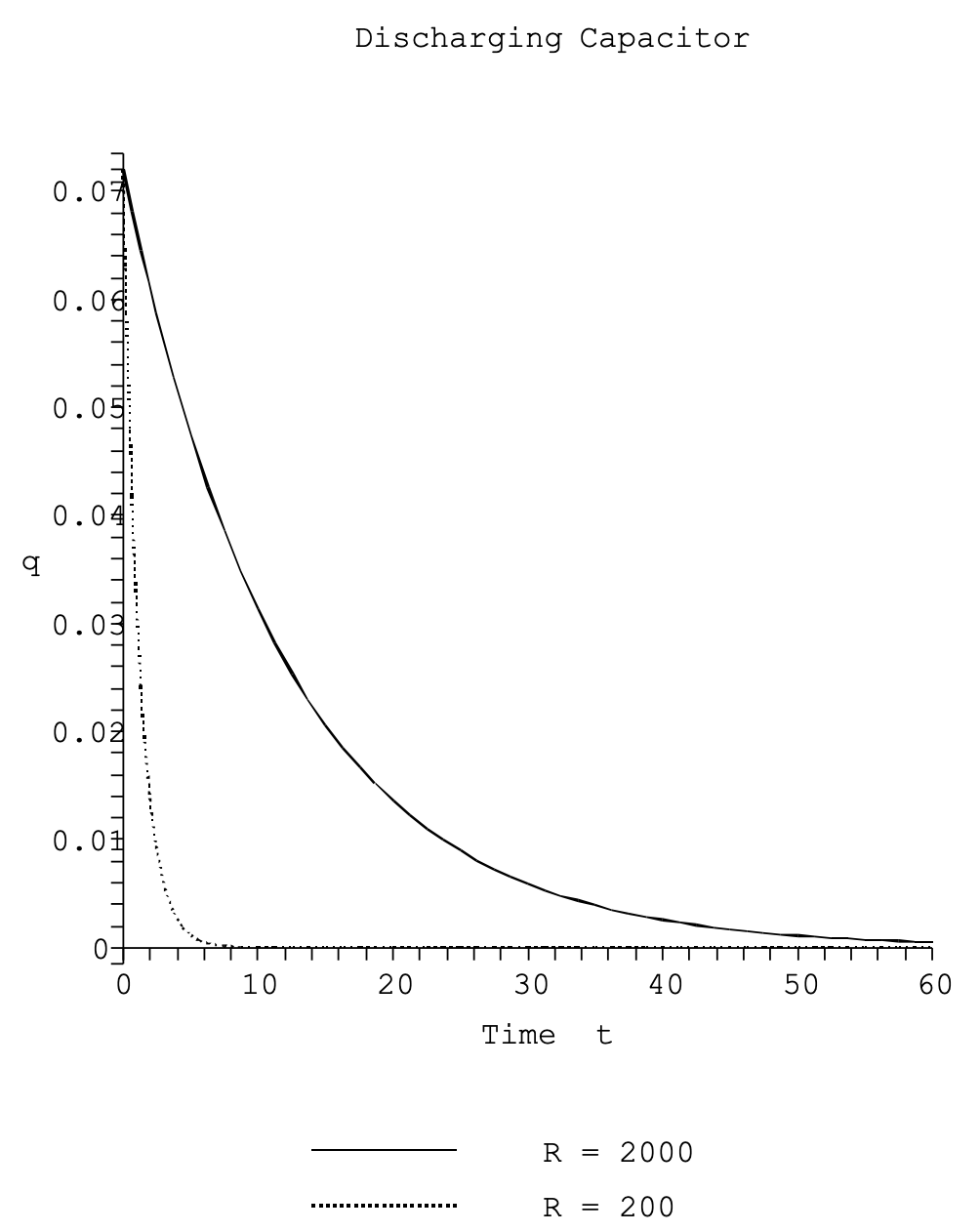
Vemos que la carga decae exponencialmente. En principio, el condensador nunca se descarga completamente. Es por eso que a menudo se le indica que coloque una derivación a través de un condensador descargado para descargarla por completo.
En la Figura 2.23 mostramos la descarga de nuestros dos circuitos RC anteriores.
Una vez más,\(\tau = RC\) determina el comportamiento. En\(t = \tau\) tenemos
\[q(\tau) = q_0e^{-1} = (0.3678794412...)q_0 \approx 0.37q_0. \nonumber \]
Entonces, en este momento el condensador sólo tiene alrededor de un tercio de su valor original.
Otro resultado sencillo viene de estudiar circuitos LC. Ahora conectaremos un condensador cargado a un inductor. En este caso, consideramos el problema de valor inicial
\[L \ddot{q}+\dfrac{1}{C} q=0, \quad q(0)=q_{0}, \dot{q}(0)=I(0)=0 \label{2.95} \]
Dividiendo la inductancia, tenemos
\[\ddot{q}+\dfrac{1}{L C} q=0 \label{2.96} \]
Esta ecuación es una ecuación de coeficiente constante de segundo orden. Es de la misma forma que la que vimos antes para el simple movimiento armónico de una masa sobre un resorte. Entonces, esperamos un comportamiento oscilatorio. La ecuación característica es
\[r^{2}+\dfrac{1}{L C}=0 \nonumber \]
Las soluciones son
\[r_{1,2}=\pm \dfrac{i}{\sqrt{L C}} \nonumber \]
Así, la solución de (2.96) es de la forma
\[q(t)=c_{1} \cos (\omega t)+c_{2} \sin (\omega t), \quad \omega=(L C)^{-1 / 2} \label{2.97} \]
Insertar los rendimientos de las condiciones iniciales
\[q(t)=q_{0} \cos (\omega t) \label{2.98} \]
Las oscilaciones que resultan son comprensibles. A medida que la carga sale de las placas, la corriente cambiante induce un campo magnético cambiante en el inductor. La energía eléctrica almacenada en el condensador cambia a energía magnética almacenada en el inductor. Sin embargo, el proceso continúa hasta que las placas se cargan con polaridad opuesta y luego el proceso comienza a la inversa. El condensador cargado luego se descarga y el condensador eventualmente vuelve a su estado original y todo el sistema repite esto una y otra vez.
La frecuencia de este simple movimiento armónico se encuentra fácilmente. Está dado por
\[f=\dfrac{\omega}{2 \pi}=\dfrac{1}{2 \pi} \dfrac{1}{\sqrt{L C}} \label{2.99} \]
A esto se le llama frecuencia de sintonización debido a su papel en los circuitos de sintonización.
Por supuesto, esta es una situación ideal. Siempre hay resistencia en el circuito, aunque solo sea una pequeña cantidad de los cables. Entonces, realmente necesitamos dar cuenta de la resistencia, o incluso agregar una resistencia. Esto lleva a un sistema un poco más complicado en el que estará presente la amortiguación.
Los circuitos más complicados son posibles al observar conexiones en paralelo, u otras combinaciones, de resistencias, condensadores e inductores. Esto dará como resultado varias ecuaciones para cada bucle en el circuito, lo que conducirá a sistemas más grandes de ecuaciones diferenciales. Un ejemplo de otra configuración de circuito se muestra en la Figura 2.24. Esto no es un problema que pueda cubrirse en el curso de física de primer año.
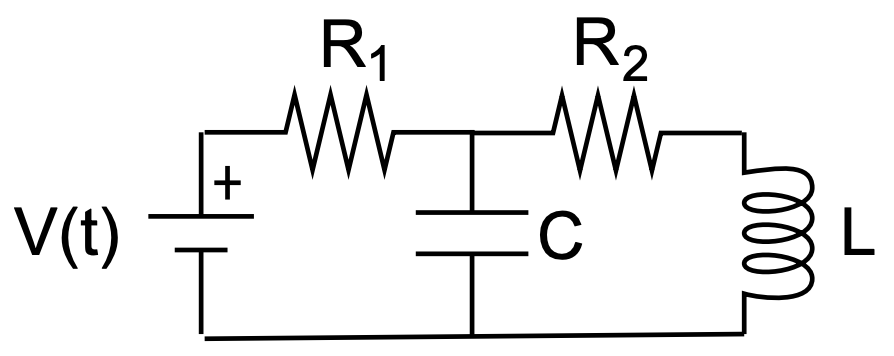
Hay dos bucles, indicados en la Figura 2.25 como atravesados en el sentido de las agujas del reloj. Para cada bucle necesitamos aplicar la Regla Loop de Kirchoff. Hay tres corrientes orientadas, etiquetadas\(I_{i}, i=1,2,3\). Correspondiente a cada corriente hay una carga cambiante, de\(q_{i}\) tal manera que
\[I_{i}=\dfrac{d q_{i}}{d t}, \quad i=1,2,3 \nonumber \]
Para el bucle uno tenemos
\[I_{1} R_{1}+\dfrac{q_{2}}{C}=V(t) \label{2.100} \]
Para bucle dos
\[I_{3} R_{2}+L \dfrac{d I_{3}}{d t}=\dfrac{q_{2}}{C} \label{2.101} \]
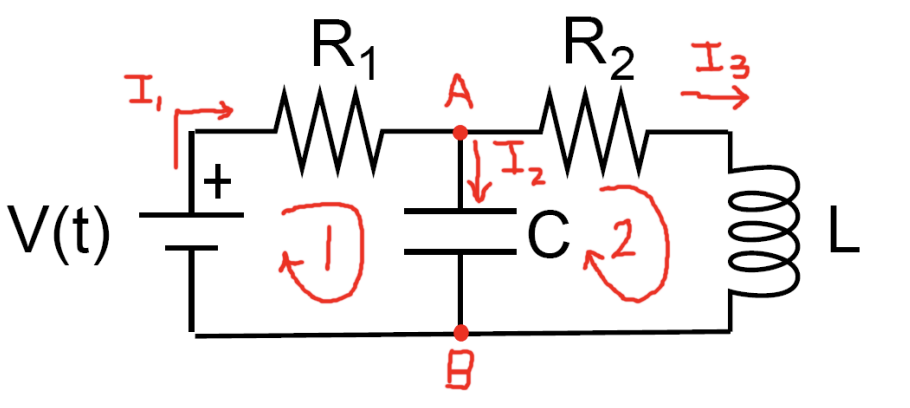
Tenemos tres funciones desconocidas para el cargo. Una vez que conocemos las funciones de carga, la diferenciación producirá las corrientes. Sin embargo, sólo tenemos dos ecuaciones. Necesitamos una tercera ecuación. Esto se encuentra de la Regla Point (Junction) de Kirchoff. Consideremos los puntos A y B de la Figura 2.25. Cualquier cargo (corriente) que ingrese a estos cruces debe ser el mismo que el cargo total (actual) que sale de los cruces. Para el punto A tenemos
\[I_{1}=I_{2}+I_{3} \label{2.102} \]
o
\[\dot{q}_{1}=\dot{q}_{2}+\dot{q}_{3} \label{2.103} \]
Las ecuaciones (2.100), (2.101) y (2.103) forman un sistema acoplado de ecuaciones diferenciales para este problema. Hay ambos derivados de primer y segundo orden involucrados. Podemos escribir todo el sistema en términos de cargos como
\ [\ begin {array} {r}
R_ {1}\ punto {q} _ {1} +\ dfrac {q_ {2}} {C} =V (t)\\
R_ {2}\ punto {q} _ {3} +L\ ddot {q} _ {3} =\ dfrac {q_ {2}} {C}\
\ punto {q} _ {1} =\ punto {q} _ {2} +\ punto {q} _ {3}
\ final {matriz}\ etiqueta {2.104}\]
La cuestión es si, o no, podemos escribir esto como un sistema de ecuaciones diferenciales de primer orden. Dado que solo hay una derivada de segundo orden, podemos introducir la nueva variable\(q_{4}=\dot{q}_{3}\). La primera ecuación se puede resolver para\(\dot{q}_{1}\). La tercera ecuación se puede resolver\(\dot{q}_{2}\) con sustituciones apropiadas para los otros términos. \(\dot{q}_{3}\)se obtiene a partir de la definición de\(q_{4}\) y la segunda ecuación se puede resolver para\(\ddot{q}_{3}\) y realizar sustituciones para obtener el sistema
\ begin {alineado}
\ punto {q} _ {1} &=\ dfrac {V} {R_ {1}} -\ dfrac {q_ {2}} {R_ {1} C}\\
\ punto {q} _ {2} &=\ dfrac {V} {R_ {1}} -\ dfrac {q_ {2}} {R_ {1} -\ dfrac {q_ {2}} {R_ {1}} C} -q_ {4}
\\ punto {q} _ {3} &=q_ {4}
\\ punto {q} _ {4} &=\ dfrac {q_ {2}} {L C} -\ dfrac {R_ {2}} {L} q_ {4}
\ final { alineado}
Entonces, tenemos un sistema no homogéneo de ecuaciones diferenciales de primer orden. En la última sección aprendimos a resolver este tipo de sistemas.
2.9.3 Asuntos amorosos
La siguiente aplicación es aquella que ha sido estudiada por varios autores como un lindo sistema que involucra relaciones. Se considera lo que sucede con los afectos que dos personas tienen el uno por el otro a lo largo del tiempo. Que\(R\) denote el cariño que Romeo tiene por Julieta y\(J\) sea el cariño que Julieta tiene por Romeo. los valores positivos indican amor y los valores negativos indican disgusto.
Un posible modelo viene dado por
\ [\ comenzar {alineado}
\ dfrac {d R} {d t} &=b J\
\ dfrac {d J} {d t} &=c R
\ end {alineado}\ etiqueta {2.105}\]
con\(b>0\) y\(c<0\). En este caso Romeo ama a Julieta cuanto más le gusta a ella. Pero Julieta retrocede cuando encuentra cada vez mayor su amor por ella.
Un sistema típico que relaciona los cambios combinados en el afecto puede modelarse como
\ [\ comenzar {alineado}
&\ dfrac {d R} {d t} =a R+b J\\
&\ dfrac {d J} {d t} =c R+d J
\ final {alineado}\ etiqueta {2.106}\]
Varios escenarios son posibles para diversas elecciones de las constantes. Por ejemplo, si\(a>0\) y\(b>0\), Romeo se emociona cada vez más por el amor de Julieta por él. Si\(c>0\) y\(d<0\), Julieta está siendo cautelosa sobre su relación con Romeo. Para valores específicos de los parámetros y condiciones iniciales, uno puede explorar este partido de un amante demasiado celoso con un amante cauteloso.
2.9.4 Modelos Predator Prey
Otro modelo común estudiado es el de especies competidoras. Por ejemplo, podríamos considerar una población de conejos y zorros. Dejados a sí mismos, los conejos tenderían a multiplicarse, así
\(\dfrac{d R}{d t}=a R\),
con\(a>0\). En tal modelo la población de conejos crecería exponencialmente. De igual manera, una población de zorros se descompondría sin que los conejos se alimentaran. Entonces, tenemos que
\[\dfrac{d F}{d t}=-b F \nonumber \]
para\(b>0\).
Ahora bien, si juntamos a estas poblaciones en una isla desierta, ellas interactuarían. Cuantos más zorros, la población de conejos disminuiría. Sin embargo, cuantos más conejos, los zorros tendrían mucho para comer y la población prosperaría. Así, podríamos modelar las poblaciones competidoras como
\ [\ comenzar {reunido}
\ dfrac {d R} {d t} =a R-c F\\
\ dfrac {d F} {d t} =-b f+d R
\ end {reunido}\ etiqueta {2.107}\]
donde todas las constantes son números positivos. El estudio de este sistema acoplado conduciría como estudio de la dinámica de estas poblaciones. Discutiremos otros sistemas (no lineales) en el próximo capítulo.
2.9.5 Problemas de mezcla
Hay muchos tipos de problemas de mezcla. Tales problemas son estándar en un primer curso sobre ecuaciones diferenciales como ejemplos de ecuaciones diferenciales de primer orden. Típicamente estos ejemplos consisten en un tanque de salmuera, agua que contiene una cantidad específica de sal con agua pura entrando y saliendo la mezcla, o el flujo de un contaminante dentro o fuera de un lago.
En general se tiene un caudal de cierta concentración de mezcla entrando en una región y una mezcla que sale de la región. El objetivo es determinar la cantidad de cosas que hay en la región en un momento dado. Esto se rige por la ecuación
Tasa de cambio de sustancia = Tasa de entrada − Tasa de salida.
Esto puede generalizarse al caso de dos tanques interconectados. Ponemos algunos ejemplos.
Un tanque de 50 galones de agua pura tiene una mezcla de salmuera con concentración de 2 libras por galón entrando a razón de 5 galones por minuto. [Ver Figura 2.26.] Al mismo tiempo, los contenidos bien mezclados drenan a razón de 5 galones por minuto. Encuentra la cantidad de sal en el tanque a tiempo t. En todos esos problemas se supone que la solución está bien mezclada en cada instante del tiempo.
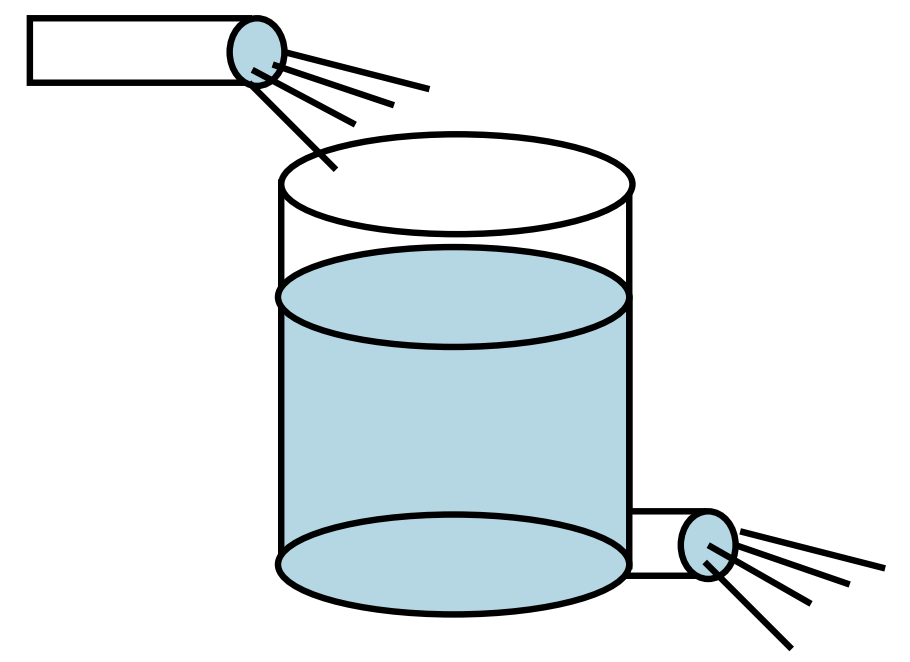
Dejar\(x(t)\) ser la cantidad de sal a la vez\(t\). Entonces la velocidad a la que aumenta la sal en el tanque se debe a la cantidad de sal que ingresa al tanque menos que la que sale del tanque. Para averiguar estas tarifas, se nota que\(dx/dt\) tiene unidades de libras por minuto. La cantidad de sal que entra por minuto viene dada por el producto de la concentración entrante multiplicada por la velocidad a la que entra la salmuera. Esto da las unidades correctas:
\[\left(2 \dfrac{\text { pounds }}{\text { gal }}\right)\left(5 \dfrac{\text { gal }}{\min }\right)=10 \dfrac{\text { pounds }}{\min }. \nonumber \]
Del mismo modo, se puede determinar la tasa de salida como
\[\left(\dfrac{x \text { pounds }}{50 \text { gal }}\right)\left(5 \dfrac{\text { gal }}{\min }\right)=\dfrac{x}{10} \dfrac{\text { pounds }}{\min } \nonumber \]
Por lo tanto, tenemos
\[\dfrac{d x}{d t}=10-\dfrac{x}{10} \nonumber \]
Esta ecuación se resuelve fácilmente usando los métodos para ecuaciones de primer orden.
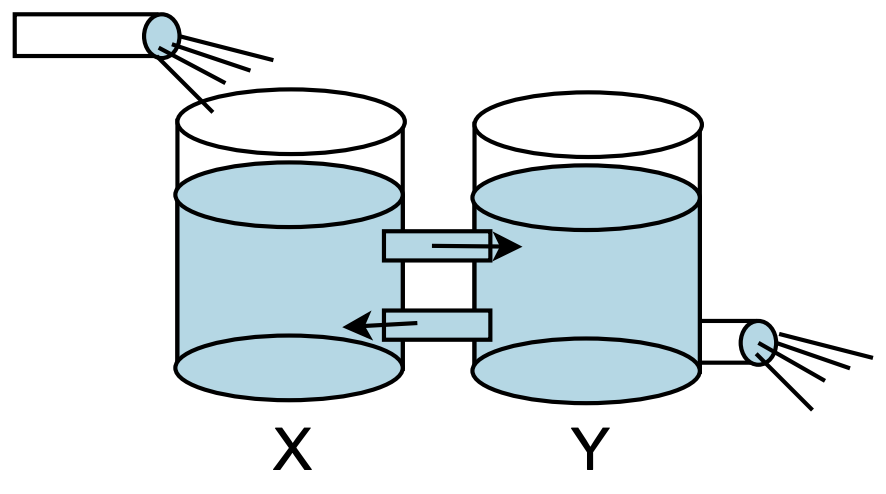
Uno tiene dos tanques conectados entre sí, etiquetados tanque\(X\) y tanque\(Y\), como se muestra en la Figura 2.27. Deje que el tanque\(X\) inicialmente tenga 100 galones de salmuera hechos con 100 libras de sal. El tanque\(Y\) inicialmente tiene 100 galones de agua pura. Ahora se bombea agua pura\(X\) al tanque a una velocidad de 2.0 galones por minuto. Parte de la mezcla de salmuera y agua pura fluye\(Y\) al tanque a 3 galones por minuto. Para mantener los niveles del tanque iguales, un galón de la\(Y\) mezcla fluye de regreso\(X\) al tanque a una velocidad de un galón por minuto y 2.0 galones por minuto drena. Encuentra la cantidad de sal en un momento dado en los tanques. ¿Qué sucede durante un largo periodo de tiempo?
En este problema configuramos dos ecuaciones. Dejar\(x(t)\) ser la cantidad de sal en el tanque\(X\) y\(y(t)\) la cantidad de sal en el tanque\(Y\). Nuevamente, analizamos cuidadosamente las tasas de entrada y salida de cada tanque para establecer el sistema de ecuaciones diferenciales. Obtenemos el sistema
\ [\ begin {alineado}
\ dfrac {d x} {d t} &=\ dfrac {y} {100} -\ dfrac {3 x} {100}\
\ dfrac {d y} {d t} &=\ dfrac {3 x} {100} -\ dfrac {3 y} {100}
\ end {alineado}\ etiqueta {2.108}\]
Se trata de un sistema de coeficientes constantes lineales y homogéneos de dos ecuaciones de primer orden, que sabemos resolver.
2.9.6 Cinética Química
Son muchos los problemas que provienen del estudio de las reacciones químicas. La reacción más simple es cuando un químico\(A\) se convierte en químico\(B\). Esto sucede a cierto ritmo,\(k>0\). Esto puede ser representado por la fórmula química
\[A \underset{k}{\longrightarrow} B \nonumber \]
En este caso tenemos que las tasas de cambio de las concentraciones de\(A,[A]\), y\(B,[B]\), están dadas por
\ [\ begin {alineado}
\ dfrac {d [A]} {d t} &=-k [A]\\
\ dfrac {d [B]} {d t} &=k [A]
\ end {alineado}\ etiqueta {2.109}\]
Piense en esto ya que es clave para entender las próximas reacciones.
Una reacción más complicada viene dada por
\[A \underset{k_{1}}{\longrightarrow} B \underset{k_{2}}{\longrightarrow} C \nonumber \]
En este caso podemos agregar a la ecuación anterior las tasas de cambio de concentraciones\([B]\) y\([C]\). El sistema resultante de ecuaciones es
\ [\ begin {alineado}
\ dfrac {d [A]} {d t} &=-k_ {1} [A]\\
\ dfrac {d [B]} {d t} &=k_ {1} [A] -k_ {2} [B],\
\ dfrac {d [C]} {d t} &=k_ {2} [B]
\ end {alineado}\ etiqueta {2.110}\]
Se pueden considerar adicionalmente reacciones en las que es posible una reacción inversa. Por lo tanto, se produce una generalización adicional para la reacción
\[A \underset{k_{1}}{\stackrel{k_{3}}{\longrightarrow}} B \underset{k_{2}}{\longrightarrow} C \nonumber \]
El sistema resultante de ecuaciones es
\ [\ begin {alineado}
\ dfrac {d [A]} {d t} &=-k_ {1} [A] +k_ {3} [B],\\
\ dfrac {d [B]} {d t} &=k_ {1} [A] -k_ {2} [B] -k_ {3} [B],\
\ dfrac {d [C]} {d t} &=k_ {2} [B].
\ end {alineado}\ etiqueta {2.111}\]
Las reacciones químicas más complicadas se discutirán en un momento posterior.
2.9.7 Epidemias
Otra área interesante de aplicación de la ecuación diferencial es en la predicción de la propagación de la enfermedad. Por lo general, se tiene una población de personas o animales susceptibles. Varios individuos infectados se introducen en la población y uno está interesado en cómo se propaga la infección y si el número de personas infectadas aumenta drásticamente o muere. Dichos modelos suelen ser no lineales y veremos lo que se llama el modelo SIR en el siguiente capítulo. En esta sección modelaremos un modelo lineal simple.
Vamos a dividir a la población en tres clases. En primer lugar,\(S(t)\) están las personas sanas, que son susceptibles a la infección. \(I(t)\)Sea el número de personas infectadas. De estas personas infectadas, algunas morirán por la infección y otras se recuperarán. Supongamos que inicialmente ahí en una persona infectada y el resto, digamos\(N\), obviamente están sanos. ¿Podemos predecir cuántas muertes han ocurrido por el tiempo\(t\)?
Intentemos modelar este problema usando el análisis compartimental que habíamos visto en los problemas de mezcla. La tasa total de cambio de cualquier población se debiría a quienes ingresan al grupo menos a los que abandonan el grupo. Por ejemplo, el número de personas sanas disminuye debido a la infección y puede aumentar cuando parte del grupo infectado se recupera. Supongamos que la tasa de infección es proporcional al número de personas sanas,\(aS\). También, suponemos que el número que se recuperan es proporcional al número de infectados,\(rI\). Así, la tasa de cambio de las personas sanas se encuentra como
\[\dfrac{d S}{d t}=-a S+r I. \nonumber \]
Que el número de muertes sea\(D(t)\). Entonces, la tasa de mortalidad podría tomarse como proporcional al número de personas infectadas. Entonces,
\[\dfrac{d D}{d t}=d I \nonumber \]
Por último, la tasa de cambio de los infecciosos se debe a que las personas sanas se infectan y a los infecciosos que se recuperan o mueren. Usando los términos correspondientes en las otras ecuaciones, podemos escribir
\[\dfrac{d I}{d t}=a S-r I-d I \nonumber \]
Este sistema lineal se puede escribir en forma de matriz.
\ [\ dfrac {d} {d t}\ left (\ begin {array} {c}
S\\
I\\
D
\ end {array}\ right) =\ left (\ begin {array} {ccc}
-a & r & 0\\
a & -d-r & 0\\
0 & d & 0
\ end {array}\ right)\ left (\ begin { matriz} {l}
S\\
I\\
D
\ final {matriz}\ derecha)\ etiqueta {2.112}\]
La ecuación de valor propio para este sistema es
\[\lambda\left[\lambda^{2}+(a+r+d) \lambda+a d\right]=0. \nonumber \]
El lector puede encontrar las soluciones de este sistema y determinar si se trata de un modelo realista.


