5.1: Introducción a la Serie de Fourier
- Page ID
- 118951
En este capítulo veremos las series trigonométricas. Anteriormente, vimos que dicha expansión en serie se producía de forma natural en la solución de la ecuación de calor y otros problemas de valor límite. En el último capítulo vimos que tales funciones podían verse como una base en un espacio vectorial dimensional infinito de funciones. Dada una función en ese espacio, ¿cuándo tendrá una representación como una serie trigonométrica? ¿Para qué valores de\(x\) convergerá? Encontrar tales series está en el corazón del análisis de Fourier, o espectral,.
Hay muchas aplicaciones que utilizan el análisis espectral. En la raíz de estos estudios está la creencia de que muchas formas de onda continuas están compuestas por una serie de armónicos. Tales ideas se remontan al estudio pitagórico de las vibraciones de las cuerdas, que llevan a su visión de un mundo de armonía. Esta idea fue llevada más allá por Johannes Kepler en su armonía de las esferas que se acercan a las órbitas planetarias. En los años 1700 otros trabajaron en la teoría de superposición para ondas vibratorias en un resorte estirado, comenzando con la ecuación de onda y conduciendo a la superposición de ondas viajeras derecha e izquierda. Esta obra la llevaron a cabo personas como John Wallis, Brook Taylor y Jean le Rond d'Alembert.
En 1742 d'Alembert resolvió la ecuación de onda
\(c^{2} \dfrac{\partial^{2} y}{\partial x^{2}}-\dfrac{\partial^{2} y}{\partial t^{2}}=0\),
donde\(y\) esta la altura de la cuerda y\(c\) es la velocidad de ola. No obstante, su solución llevó a sí mismo y a otros, como Leonhard Euler y Daniel Bernoulli, a investigar qué “funciones” podrían ser las soluciones de esta ecuación. De hecho, esto condujo a un acercamiento más riguroso al estudio del análisis al primero acercarse al concepto de una función. Por ejemplo, en 1749 Euler buscó la solución para una cuerda desplumada en cuyo caso la condición inicial\(y(x, 0)=h(x)\) tiene una derivada discontinua!
En 1753 Daniel Bernoulli vio las soluciones como una superposición de vibraciones simples, o armónicos. Tales superposiciones equivalían a buscar soluciones de la forma
\(y(x, t)=\sum_{k} a_{k} \sin \dfrac{k \pi x}{L} \cos \dfrac{k \pi c t}{L}\),
donde la cadena se extiende sobre el intervalo\([0, L]\) con extremos fijos en\(x=0\) y\(x=L\). Sin embargo, las condiciones iniciales para tales superposiciones son
\[y(x, 0)=\sum_{k} a_{k} \sin \dfrac{k \pi x}{L}. \nonumber \]
Se determinó que muchas funciones no podían ser representadas por un número finito de armónicos, incluso para la cuerda simplemente arrancada dada por una condición inicial de la forma
\ (y (x, 0) =\ izquierda\ {\ comenzar {matriz} {cl}
c x, & 0\ leq x\ leq L/2\\
c (L-x), & L/2\ leq x\ leq L
\ final {matriz}\ derecha.\)
Así, la solución consiste generalmente en una serie infinita de funciones trigonométricas.
Tales expansiones de series también fueron importantes en la solución de Joseph Fourier de la ecuación de calor. El uso de tales expansiones de Fourier se convirtió en una herramienta importante en la solución de ecuaciones diferenciales parciales lineales, como la ecuación de onda y la ecuación de calor. Como se ve en el último capítulo, utilizando el Método de Separación de Variables, permite reducir problemas dimensionales superiores a varios problemas de valor límite unidimensional. Sin embargo, estos estudios conducen a preguntas muy importantes, que a su vez abrieron las puertas a campos enteros de análisis. Algunos de los problemas planteados fueron
1. ¿Qué funciones se pueden representar como la suma de funciones trigonométricas?
2. ¿Cómo se puede representar una función con derivadas discontinuas por una suma de funciones suaves, como las sumas anteriores?
3. ¿Tales sumas infinitas de funciones trigonométricas a convergen realmente con las funciones que representan?
Las sumas sobre las funciones sinusoidales ocurren naturalmente en la música y en el estudio de las ondas sonoras. Una nota pura se puede representar como
\(y(t)=A \sin (2 \pi f t)\),
donde\(A\) está la amplitud,\(f\) es la frecuencia en hercios\((\mathrm{Hz})\), y\(t\) es el tiempo en segundos. La amplitud está relacionada con el volumen, o intensidad, del sonido. Cuanto mayor es la amplitud, más fuerte es el sonido. En la Figura 5.1 se muestran parcelas de dos de esos tonos con\(f=2 \mathrm{~Hz}\) en la gráfica superior y\(f=5 \mathrm{~Hz}\) en la inferior.
A continuación, consideramos lo que sucede cuando agregamos varios tonos puros. Después de todo, la mayoría de los sonidos que escuchamos son de hecho una combinación de tonos puros con
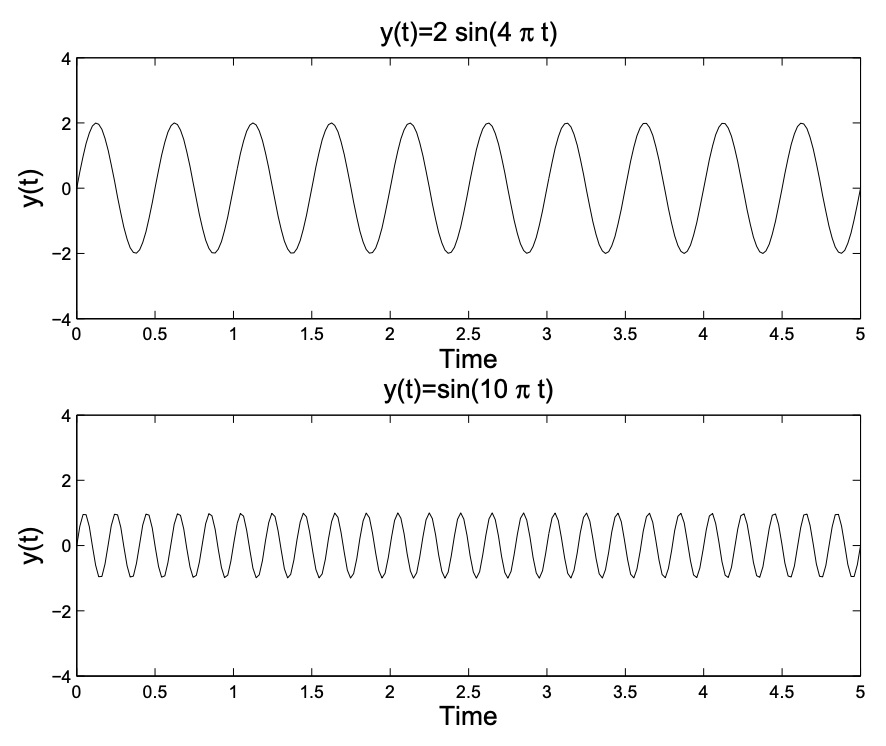
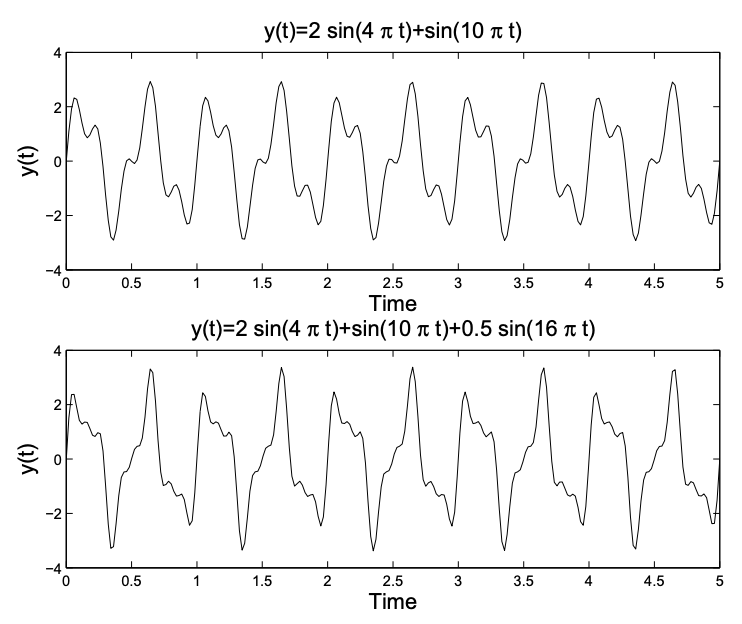
diferentes amplitudes y frecuencias. En la Figura 5.2 vemos lo que sucede cuando agregamos varias sinusoides. Tenga en cuenta que a medida que uno agrega más y más tonos con diferentes características, la señal resultante se vuelve más complicada. Sin embargo, todavía tenemos una función de tiempo. En este capítulo vamos a preguntar: “Dada una función\(f(t)\), ¿podemos encontrar un conjunto de funciones sinusoidales cuya suma converja a\(f(t)\)?”
Al observar las superposiciones en la Figura 5.2, vemos que las sumas rinden funciones que parecen ser periódicas. Esto no va a ser inesperado. Recordamos que una función periódica es aquella en la que los valores de la función se repiten sobre el dominio de la función. La longitud de la parte más pequeña del dominio que se repite se denomina período. Esto lo podemos definir con mayor precisión.
Se dice que una función es periódica con punto\(T\) si\(f(t+T)=f(t)\) para todos\(t\) y el menor número positivo de este tipo\(T\) se llama el período.
Por ejemplo, consideramos las funciones utilizadas en la Figura 5.2. Empezamos con\(y(t)=2 \sin (4 \pi t)\). Recuerda de tus primeros estudios de funciones trigonométricas que se puede determinar el periodo dividiendo el coeficiente de\(t\) en\(2 \pi\) para obtener el periodo. En este caso tenemos
\[T=\dfrac{2 \pi}{4 \pi}=\dfrac{1}{2} \nonumber \]
Mirando la gráfica superior en la Figura 5.1 podemos verificar este resultado. (Se puede contar el número completo de ciclos en la gráfica y dividirlo en el tiempo total para obtener un valor más preciso del periodo).
En general, si\(y(t)=A \sin (2 \pi f t)\), el periodo se encuentra como
\[T=\dfrac{2 \pi}{2 \pi f}=\dfrac{1}{f} \nonumber \]
Por supuesto, este resultado tiene sentido, ya que la unidad de frecuencia, el hertz, también se define como\(s^{-1}\), o ciclos por segundo.
Volviendo a las superposiciones en la Figura 5.2, tenemos que\(y(t)= \sin (10 \pi t)\) tiene un periodo de\(0.2 \mathrm{~Hz}\) y\(y(t)=\sin (16 \pi t)\) tiene un periodo de\(0.125 \mathrm{~Hz}\). Las dos superposiciones conservan el mayor periodo de las señales agregadas, que es\(0.5 \mathrm{~Hz}\).
Nuestro objetivo será comenzar con una función y luego determinar las amplitudes de los sinusoides simples necesarios para sumar a esa función. En primer lugar, veremos que esto podría implicar un número infinito de tales términos. Así, estaremos estudiando una serie infinita de funciones sinusoidales.
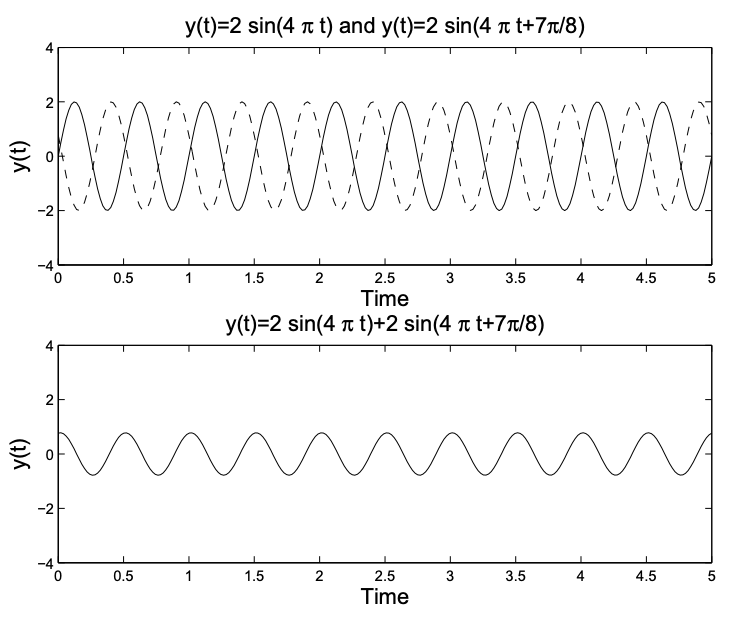
En segundo lugar, encontraremos que el uso justo de funciones sinusoidales tampoco será suficiente. Esto se debe a que podemos agregar funciones sinusoidales que no necesariamente alcanzan un pico al mismo tiempo. Consideraremos dos señales que se originan en diferentes momentos. Esto es similar a cuando tu profesor de música haría que secciones de la clase cantaran una canción como “Row, Row, Row your Boat” comenzando en momentos ligeramente diferentes.
Podemos agregar fácilmente funciones sinusoidales cambiadas. En la Figura 5.3 se muestran las funciones\(y(t)=2 \sin (4 \pi t)\)\(y(t)=2 \sin (4 \pi t+7 \pi / 8)\) y su suma. Tenga en cuenta que esta función sinusoidal desplazada se puede escribir como\(y(t)=2 \sin (4 \pi(t+7 / 32))\). Así, esto corresponde a un cambio de tiempo de\(-7 / 8\).
Entonces, deberíamos dar cuenta de las funciones sinusoidales cambiadas en nuestra suma general. Por supuesto, entonces necesitaríamos determinar el desplazamiento de tiempo desconocido así como las amplitudes de las funciones sinusoidales que componen nuestra señal,\(f(t)\). Si bien este es un enfoque que algunos investigadores utilizan para analizar señales, existe un enfoque más común. Esto resulta de otra reelaboración de la función desplazada. Considere la función desplazada general
\[y(t)=A \sin (2 \pi f t+\phi). \nonumber \]
Tenga en cuenta que\(2 \pi f t+\phi\) se llama la fase de nuestra función sinusoidal y\(\phi\) se llama el desplazamiento de fase. Podemos utilizar nuestra identidad trigonométrica para el seno de la suma de dos ángulos para obtener
\[y(t)=A \sin (2 \pi f t+\phi)=A \sin (\phi) \cos (2 \pi f t)+A \cos (\phi) \sin (2 \pi f t). \nonumber \]
Definiendo\(a=A \sin (\phi)\) y\(b=A \cos (\phi)\), podemos reescribir esto como
\[y(t)=a \cos (2 \pi f t)+b \sin (2 \pi f t) \nonumber \]
Así, vemos que nuestra señal es una suma de funciones sinusoidales y cosenales con la misma frecuencia y diferentes amplitudes. Si podemos encontrar\(a\) y\(b\), entonces podemos determinar fácilmente\(A\) y\(\phi\):
\[A=\sqrt{a^{2}+b^{2}} \quad \tan \phi=\dfrac{b}{a}. \nonumber \]
Ahora estamos en condiciones de exponer nuestro objetivo en este capítulo.
Dada una señal\(f(t)\), nos gustaría determinar su contenido de frecuencia averiguando qué combinaciones de senos y cosenos de frecuencias y amplitudes variables sumarán a la función dada. Esto se llama Análisis de Fourier.


