5.2: Serie Trigonométrica de Fourier
- Page ID
- 118963
Como hemos visto en el último apartado, nos interesa encontrar representaciones de funciones en términos de senos y cosenos. Dada una función\(f(x)\) buscamos una representación en la forma
\[f(x) \sim \dfrac{a_{0}}{2}+\sum_{n=1}^{\infty}\left[a_{n} \cos n x+b_{n} \sin n x\right]. \label{5.1} \]
Observe que hemos optado por dejar caer la referencia a la forma de frecuencia de la fase. Esto conducirá a una discusión más sencilla por ahora y siempre se puede hacer la transformación a la\(n x=2 \pi f_{n} t\) hora de aplicar estas ideas a las aplicaciones.
La representación de la serie en la Ecuación (5.1) se denomina serie trigonométrica de Fourier. Simplemente nos referiremos a esto como una serie de Fourier por ahora. El conjunto de constantes\(a_{0}, a_{n}, b_{n}, n=1,2, \ldots\) se denominan coeficientes de Fourier. El término constante se elige en esta forma para simplificar los cálculos posteriores, aunque algunos otros autores optan por escribir el término constante como\(a_{0}\). Nuestro objetivo es encontrar la representación de la serie de Fourier dada\(f(x)\). Habiendo encontrado la representación de la serie de Fourier, nos interesará determinar cuándo converge la serie de Fourier y a qué función converge.
De nuestra discusión en la última sección, vemos que la serie infinita es periódica. El mayor periodo de los términos proviene de los\(n=1\) términos. Los periodos de\(\cos x\) y\(\sin x\) son\(T=2 \pi\). Así, la serie de Fourier tiene periodo\(2 \pi\). Esto significa que la serie debe ser capaz de representar funciones que son periódicas de periodo\(2 \pi\).
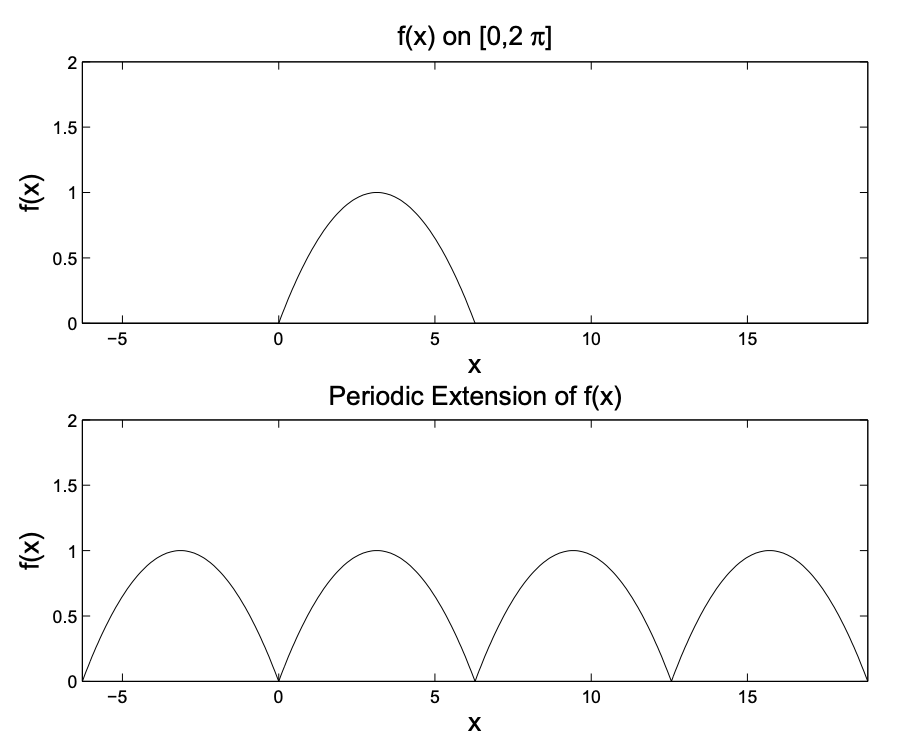
Si bien esto parece restrictivo, también podríamos considerar funciones que se definen a lo largo de un periodo. En la Figura 5.4 mostramos una función definida en\([0,2 \pi]\). En la misma figura, mostramos su extensión periódica. Estas son solo copias de la función original desplazada por el periodo y pegadas entre sí. La extensión ahora puede ser representada por una serie de Fourier y restringir la serie de Fourier a\([0,2 \pi]\) dará una representación de la función original. Por lo tanto, primero consideraremos representaciones de series de Fourier de funciones definidas en este intervalo. Tenga en cuenta que podríamos considerar fácilmente funciones definidas en\([-\pi, \pi]\) o cualquier intervalo de longitud\(2 \pi\).
La representación de la serie de Fourier de\(f(x)\) definido en\([0,2 \pi]\) cuando existe, viene dada por (5.1) con coeficientes de Fourier
\ [\ begin {alineado}
a_ {n} &=\ dfrac {1} {\ pi}\ int_ {0} ^ {2\ pi} f (x)\ cos n x d x,\ quad n=0,1,2,\ ldots\\
b_ {n} &=\ dfrac {1} {\ pi}\ int_ {0} ^ {2\ pi} f (x)\ sin n x d x,\ quad n=1,2,\ lpuntos
\ final {alineado}\ etiqueta {5.2}\]
Estas expresiones para los coeficientes de Fourier se obtienen considerando integraciones especiales de la serie de Fourier. Veremos las derivaciones\(a_{n}\) de los 's. primero obtenemos\(a_{0}\).
Comenzamos integrando la serie de Fourier término por término en la Ecuación (5.1).
\[\int_{0}^{2 \pi} f(x) d x=\int_{0}^{2 \pi} \dfrac{a_{0}}{2} d x+\int_{0}^{2 \pi} \sum_{n=1}^{\infty}\left[a_{n} \cos n x+b_{n} \sin n x\right] d x \label{5.3} \]
Suponemos que podemos integrar la suma infinita término por término. Entonces tenemos que computar
\ [\ begin {array} {r}
\ int_ {0} ^ {2\ pi}\ dfrac {a_ {0}} {2} d x=\ dfrac {a_ {0}} {2} (2\ pi) =\ pi a_ {0}\
\ int_ {0} ^ {2\ pi}\ cos n x d x=\ izquierda [\ dfrac {\ sin n x} {n}\ derecha] _ {0} ^ {2\ pi} =0\\
\ int_ {0} ^ {2\ pi}\ sin n x d x=\ izquierda [\ dfrac {-\ cos n x} {n}\ derecha] _ {0} ^ {2\ pi} =0
\ fin {matriz}\ etiqueta {5.4}\]
A partir de estos resultados vemos que solo un término en la suma integrada no desaparece dejando
\[\int_{0}^{2 \pi} f(x) d x=\pi a_{0} \nonumber \]
Esto confirma el valor para\(a_{0}\).
A continuación, tenemos que encontrar\(a_{n}\). Multiplicaremos la serie de Fourier (5.1) por\(\cos m x\) para algún entero positivo\(m\). Esto es como multiplicar por\(\cos 2 x, \cos 5 x\), etc. Estamos multiplicando por todas las\(\cos mx\) funciones posibles para diferentes enteros\(m\) todos al mismo tiempo. Veremos que esto nos permitirá resolver para los\(a_n\)'s.
Encontramos que la suma integrada de los tiempos de la serie\(\cos mx\) viene dada por
\ [\ begin {alineado}
\ int_ {0} ^ {2\ pi} f (x)\ cos m x d x &=\ int_ {0} ^ {2\ pi}\ dfrac {a_ {0}} {2}\ cos m x d x\\
&+\ int_ {0} ^ {2\ pi}\ sum_ {n=1} ^ {\ infty} izquierda\ [a_ {n}\ cos n x+b_ {n}\ sin n x\ derecha]\ cos m x d x
\ fin {alineado}\ etiqueta {5.5}\]
Integrando término por término, el lado derecho se convierte
\[\dfrac{a_{0}}{2} \int_{0}^{2 \pi} \cos m x d x+\sum_{n=1}^{\infty}\left[a_{n} \int_{0}^{2 \pi} \cos n x \cos m x d x+b_{n} \int_{0}^{2 \pi} \sin n x \cos m x d x\right] \text {. } \label{5.6} \]
Eso ya lo hemos establecido\(\int_{0}^{2 \pi} \cos m x d x=0\), lo que implica que el primer término se desvanece.
A continuación necesitamos computar integrales de productos de senos y cosenos. Esto requiere que hagamos uso de algunas identidades trigonométricas. Si bien has visto tales integrales antes en tu clase de cálculo, revisaremos cómo llevar a cabo dichas integrales. Para referencia futura, enumeramos varias identidades útiles, algunas de las cuales probaremos en el camino.
\[\sin (x \pm y) =\sin x \cos y \pm \sin y \cos x \label{5.7} \]
\[\cos (x \pm y) =\cos x \cos y \mp \sin x \sin y \label{5.8} \]
\[\sin ^{2} x =\dfrac{1}{2}(1-\cos 2 x) \label{5.9} \]
\[\cos ^{2} x =\dfrac{1}{2}(1+\cos 2 x) \label{5.10} \]
\[\sin x \sin y =\dfrac{1}{2}(\cos (x-y)-\cos (x+y)) \label{5.11} \]
\[\cos x \cos y =\dfrac{1}{2}(\cos (x+y)+\cos (x-y)) \label{5.12} \]
\[\sin x \cos y =\dfrac{1}{2}(\sin (x+y)+\sin (x-y)) \label{5.13} \]
Primero queremos evaluar\(\int_{0}^{2 \pi} \cos n x \cos m x d x\). Esto lo hacemos usando la identidad del producto. Esto lo habíamos hecho en el último capítulo, pero vamos a repetir la derivación para beneficio del lector. Recordemos las fórmulas de adición para cosenos:
\[\cos (A+B)=\cos A \cos B-\sin A \sin B \nonumber \]
\[\cos (A-B)=\cos A \cos B+\sin A \sin B \nonumber \]
La adición de estas ecuaciones da
\[2 \cos A \cos B=\cos (A+B)+\cos (A-B). \nonumber \]
Podemos usar esta identidad con\(A=m x\) y\(B=n x\) para completar la integración.
Tenemos
\ [\ begin {alineado}
\ int_ {0} ^ {2\ pi}\ cos n x\ cos m x d x &=\ dfrac {1} {2}\ int_ {0} ^ {2\ pi} [\ cos (m+n) x+\ cos (m-n) x] d x\\
&=\ dfrac {1} {2}\ izquierda [\ dfrac {\ sin (m+n) x} {m+n} +\ dfrac {\ sin (m-n) x} {m-n}\ derecha] _ {0} ^ {2\ pi}\\
&=0.
\ end {alineado}\ etiqueta {5.14}\]
Hay una advertencia al hacer tales integrales. ¿Y si uno de los denominadores\(m \pm n\) desaparece? Para nuestro problema\(m+n \neq 0\), ya que ambos\(m\) y\(n\) son enteros positivos. Sin embargo, es posible para\(m=n\). Esto quiere decir que la fuga de lo integral sólo puede ocurrir cuando\(m \neq n\). Entonces, ¿qué podemos hacer con respecto al\(m=n\) caso? Una forma es comenzar de cero con nuestra integración. (Otra forma es computar el límite como\(n\) aproximaciones\(m\) en nuestro resultado y usar la Regla de L'Hopital. ¡Pruébalo!)
Entonces, pues\(n=m\) tenemos que computar\(\int_{0}^{2 \pi} \cos ^{2} m x d x\). Esto también se puede manejar usando una identidad trigonométrica. Recordemos que
\[\cos ^{2} \theta=\dfrac{1}{2}(1+\cos 2 \theta \text {. }) \nonumber \]
Insertando esto en la integral, encontramos
\ [\ begin {alineado}
\ int_ {0} ^ {2\ pi}\ cos ^ {2} m x d x &=\ dfrac {1} {2} {2}\ int_ {0} ^ {2\ pi}\ izquierda (1+\ cos ^ {2} 2 m x\ derecha) d x\
&=\ dfrac {1} {2}\ izquierda [x+\ dfrac {1} {2 m}\ sin 2 m x\ derecha] _ {0} ^ {2\ pi}\\
&=\ dfrac {1} {2} (2\ pi) =\ pi
\ final {alineado}\ etiqueta {5. 15}\]
Para resumir, hemos demostrado que
\ [\ int_ {0} ^ {2\ pi}\ cos n x\ cos m x d x=\ izquierda\ {\ comenzar {matriz} {l}
0, m\ neq n\\
\ pi, m=n
\ end {array}\ derecha. \ label {5.16}\]
Esto es cierto para\(m, n=0,1, \ldots\). [¿Por qué incluimos\(m, n=0\)?] Cuando tenemos tal conjunto de funciones, se dice que son un conjunto ortogonal sobre el intervalo de integración.
Se dice que un conjunto de funciones (reales)\(\left\{\phi_{n}(x)\right\}\) son ortogonales en\([a, b]\) if\(\int_{a}^{b} \phi_{n}(x) \phi_{m}(x) d x=0\) when\(n \neq m\). Además, si también tenemos eso\(\int_{a}^{b} \phi_{n}^{2}(x) d x=1\), estas funciones se denominan ortonormales.
El conjunto de funciones\(\{\cos n x\}_{n=0}^{\infty}\) son ortogonales en\([0,2 \pi]\). En realidad, son ortogonales en cualquier intervalo de longitud\(2 \pi\). Podemos hacerlos ortonormales dividiendo cada función por\(\sqrt{\pi}\) como lo indica la Ecuación (5.15).
La noción de ortogonalidad es en realidad una generalización de la ortogonalidad de los vectores en espacios vectoriales de dimensiones finitas. La integral\(\int_{a}^{b} f(x) f(x) d x\) es la generalización del producto punto, y se llama el producto escalar de\(f(x)\) y\(g(x)\), que se consideran vectores en un espacio vectorial dimensional infinito abarcado por un conjunto de funciones ortogonales. Pero ese es otro tema para después.
Volviendo a la evaluación de las integrales en la ecuación (5.6), todavía tenemos que evaluar\(\int_{0}^{2 \pi} \sin n x \cos m x d x\). Esto también se puede evaluar utilizando identidades trigonométricas. En este caso, necesitamos una identidad que involucre productos de senos y cosenos. Dichos productos ocurren en las fórmulas de adición para funciones sinusoidales:
\ comenzar {alineado}
&\ sin (A+B) =\ sin A\ cos B+\ sin B\ cos A\\
&\ sin (A-B) =\ sin A\ cos B-\ sin B\ cos A
\ fin {alineado}
Añadiendo estas ecuaciones, encontramos que
\[\sin (A+B)+\sin (A-B)=2 \sin A \cos B. \nonumber \]
Ajuste\(A=n x\) y\(B=m x\), nos encontramos con que
\ [\ comenzar {alineado}
\ int_ {0} ^ {2\ pi}\ sin n x\ cos m x d x &=\ dfrac {1} {2}\ int_ {0} ^ {2\ pi} [\ sin (n+m) x+\ sin (n-m) x] d x\\
&=\ dfrac {1} {2}\ izquierda [\ dfrac {-\ cos (n+m) x} {n+m} +\ dfrac {-\ cos (n-m) x} {n-m}\ derecha] _ {0} ^ {2\ pi}\\
& =( -1+1) + (-1+1) =0.
\ end {alineado}\ etiqueta {5.17}\]
Para estas integrales también debemos tener cuidado al establecer\(n=m\). En este caso especial, tenemos las integrales
\[\int_{0}^{2 \pi} \sin m x \cos m x d x=\dfrac{1}{2} \int_{0}^{2 \pi} \sin 2 m x d x=\dfrac{1}{2}\left[\dfrac{-\cos 2 m x}{2 m}\right]_{0}^{2 \pi}=0. \nonumber \]
Finalmente, podemos terminar nuestra evaluación de (5.6). Hemos determinado que todo menos una integral se desvanece. En ese caso,\(n=m\). Esto nos deja con
\[\int_{0}^{2 \pi} f(x) \cos m x d x=a_{m} \pi \nonumber \]
Resolviendo para\(a_{m}\) da
\[a_{m}=\dfrac{1}{\pi} \int_{0}^{2 \pi} f(x) \cos m x d x \nonumber \]
Como esto es cierto para todos\(m=1,2, \ldots\), hemos probado esta parte del teorema. La única parte que queda es encontrar los\(b_{n}\)'s Esto se dejará como un ejercicio para el lector.
Ahora consideramos ejemplos de encontrar coeficientes de Fourier para funciones dadas. En todos estos casos definimos\(f(x)\) sobre\([0,2 \pi]\).
Primero calculamos las integrales para los coeficientes de Fourier.
\ [\ begin {alineado}
&a_ {0} =\ dfrac {1} {\ pi}\ int_ {0} ^ {2\ pi} 3\ cos 2 x d x=0\\
&a_ {n} =\ dfrac {1} {\ pi}\ int_ {0} ^ {2\ pi} 3\ cos 2 x\ cos cuádruple n x d x=0,\ n\ neq 2\\
&a_ {2} =\ dfrac {1} {\ pi}\ int_ {0} ^ {2\ pi} 3\ cos ^ {2} 2 x d x=3\\
&b_ {n} =\ dfrac {1} {\ pi}\ int_ {0} ^ {2\ pi} 3\ cos 2 x\ sin n x d x=0,\ forall n
\ end {alineado}\ etiqueta {5.18}\]
Por lo tanto, tenemos que el único coeficiente de no fuga es\(a_{2}=3\). Entonces hay un término y\(f(x)=3 \cos 2 x\). Bueno, deberíamos haber sabido esto antes de hacer todas estas integrales. Entonces, si tenemos una función expresada simplemente en términos de sumas de senos simples y cosenos, entonces debería ser fácil anotar los coeficientes de Fourier sin mucho trabajo.
Podríamos determinar los coeficientes de Fourier integrándolos como en el último ejemplo. Sin embargo, es más fácil usar identidades trigonométricas. Sabemos que
\[\sin ^{2} x=\dfrac{1}{2}(1-\cos 2 x)=\dfrac{1}{2}-\dfrac{1}{2} \cos 2 x. \nonumber \]
No hay términos sinusoidales, entonces\(b_{n}=0, n=1,2, \ldots\) hay un término constante, implicando\(a_{0} / 2=1 / 2\). Entonces,\(a_{0}=1\). Hay un\(\cos 2 x\) término, que corresponde a\(n=2\), entonces\(a_{2}=-\dfrac{1}{2}\). Eso deja\(a_{n}=0\) para\(n \neq 0,2\).
Este ejemplo tomará un poco más de trabajo. No podemos pasar por alto la evaluación de ninguna integral en este momento. Esta función es discontinua, por lo que tendremos que computar cada integral dividiendo la integración en dos integrales, una encima\([0, \pi]\) y otra sobre\([\pi, 2 \pi]\).
\ [\ begin {alineado}
a_ {0} &=\ dfrac {1} {\ pi}\ int_ {0} ^ {2\ pi} f (x) d x\\
&=\ dfrac {1} {\ pi}\ int_ {0} ^ {\ pi} d x+\ dfrac {1} {\ pi}\ int_ {\ pi} ^ {2\ pi} (-1) d x\\
&=\ dfrac {1} {\ pi} (\ pi) +\ dfrac {1} {\ pi} (-2\ pi+\ pi) =0
\ final {alineado}\ etiqueta {5.19}\]
\ [\ begin {alineado}
a_ {n} &=\ dfrac {1} {\ pi}\ int_ {0} ^ {2\ pi} f (x)\ cos n x d x\\
&=\ dfrac {1} {\ pi}\ left [\ int_ {0} ^ {\ pi} ^ {\ pi}\ cos n x d x-\ int_ {\ pi}\ ^ {2\ pi}\ cos n x d x\ derecha]\\
&=\ dfrac {1} {\ pi}\ izquierda [\ izquierda (\ dfrac {1} {n}\ sin n x\ derecha) _ {0} ^ {\ pi} -\ izquierda (\ dfrac {1} {n} \ sin n x\ derecha) _ {\ pi} ^ {2\ pi}\ derecha]\\
&=0.
\ end {alineado}\ etiqueta {5.20}\]
\ [\ begin {alineado}
b_ {n} &=\ dfrac {1} {\ pi}\ int_ {0} ^ {2\ pi} f (x)\ sin n x d x\
&=\ dfrac {1} {\ pi}\ left [\ int_ {0} ^ {\ pi} ^ {\ pi}\ sin n x d x-\ int_ {\ pi} ^ {2\ pi}\ sin n x d x\ derecha]\\
&=\ dfrac {1} {\ pi}\ izquierda [\ izquierda (-\ dfrac {1} {n}\ cos n x\ derecha) _ {0} ^ {\ pi} +\ izquierda (\ dfrac {1} {n} \ cos n x\ derecha) _ {\ pi} ^ {2\ pi}\ derecha]\\
&=\ dfrac {1} {\ pi}\ izquierda [-\ dfrac {1} {n}\ cos n\ pi+\ dfrac {1} {n} +\ dfrac {1} {n} -\ dfrac {1} {n}\ cos n\ pi\ derecha]\\
&=\ dfrac {2} {n\ pi} (1-\ cos n\ pi)
\ final {alineado}\ etiqueta {5.21}\]
Hemos encontrado los coeficientes de Fourier para esta función. Antes de insertarlos en la serie de Fourier (5.1), notamos que\(\cos n \pi=(-1)^{n}\). Por lo tanto,
\ [1-\ cos n\ pi=\ left\ {\ begin {array} {l}
0, n\ text {par}\\
2, n\ text {impar}
\ end {array}\ right. \ label {5.22}\]
Entonces, la mitad de los\(b_{n}\)'s son cero. Si bien podríamos escribir la representación de la serie de Fourier como
\[f(x) \sim \dfrac{4}{\pi} \sum_{n=1, \text { odd }}^{\infty} \dfrac{1}{n} \sin n x \nonumber \]
podríamos dejar\(n=2 k-1\) y escribir
\(f(x)=\dfrac{4}{\pi} \sum_{k=1}^{\infty} \dfrac{\sin (2 k-1) x}{2 k-1}\),
Pero, ¿converge esta serie? ¿Converge a\(f(x)\)? Discutiremos esta cuestión más adelante en el capítulo.


