1.1: Introducción a R
- Page ID
- 111741
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)El cálculo es el estudio de las relaciones funcionales y cómo cambian las cantidades relacionadas entre sí. En su primera exposición al cálculo, el foco principal de su atención fue en las funciones que involucran una sola variable independiente y una sola variable dependiente. Para tal función\(f,\) una sola entrada de número real\(x\) determina un único valor de salida\(f(x) .\) Sin embargo, muchas de las funciones de importancia tanto dentro de las matemáticas mismas como en la aplicación de las matemáticas al resto del mundo involucran muchas variables simultáneamente. Por ejemplo, frecuentemente en física la función que describe la fuerza que actúa sobre un objeto que se mueve en el espacio depende de tres variables, las tres coordenadas que describen la ubicación del objeto. Si la función de fuerza también varía con el tiempo, entonces la fuerza depende de cuatro variables. Además, la salida de la función de fuerza involucrará en sí misma tres variables, las tres componentes de coordenadas de la fuerza. De ahí que la función de fuerza sea tal que toma tres, o cuatro, variables para entrada y salidas tres variables. Funciones mucho más complicadas son fáciles de imaginar: el producto nacional bruto de un país es función de miles de variables con una sola variable como salida, un horario de la aerolínea es una función con miles de insumos (ciudades, aviones y personas a programar, así como otras variables como los costos de combustible y los horarios de las aerolíneas competidoras) y quizás cientos de salidas (las rutas particulares voladas, junto con sus tiempos). Aunque tales funciones pueden parecer al principio mucho más difíciles de trabajar que las funciones del cálculo de una sola variable, veremos que a menudo seremos capaces de reducir los problemas que involucran funciones de varias variables a problemas relacionados que involucran solo funciones de una sola variable, problemas que podemos luego manejar usando técnicas ya familiares.
Por definición, una función toma un único valor de entrada y lo asocia con un único valor de salida. Por lo tanto, aunque en este libro las entradas a nuestras funciones a menudo implicarán varias variables, al igual que las salidas, sin embargo, vamos a querer considerar la entrada y salida de una función como puntos únicos en algún espacio multidimensional. Esto es natural en el caso de, por ejemplo, la función de fuerza descrita anteriormente, donde la entrada es un punto en el espacio tridimensional, cuatro si necesitamos usar el tiempo, pero requiere alguna abstracción matemática si queremos considerar la entrada a la función del producto nacional bruto como un punto en algún espacio de muchos miles de dimensiones. Debido a que incluso la geometría del espacio bidimensional y tridimensional puede ser en algunos aspectos nueva para usted, utilizaremos este capítulo para estudiar la geometría del espacio multidimensional antes de proceder al estudio del cálculo propio en el Capítulo 2.
A lo largo del libro dejaremos\(\mathbb{R}\) denotar el conjunto de números reales.
Definición: Espacio Euclideano
Por espacio euclidiano n-dimensional nos referimos al conjunto
\[\mathbb{R}^{n}=\left\{\left(x_{1}, x_{2}, \ldots, x_{n}\right): x_{i} \in \mathbb{R}, i=1,2, \ldots, n\right\}.\]
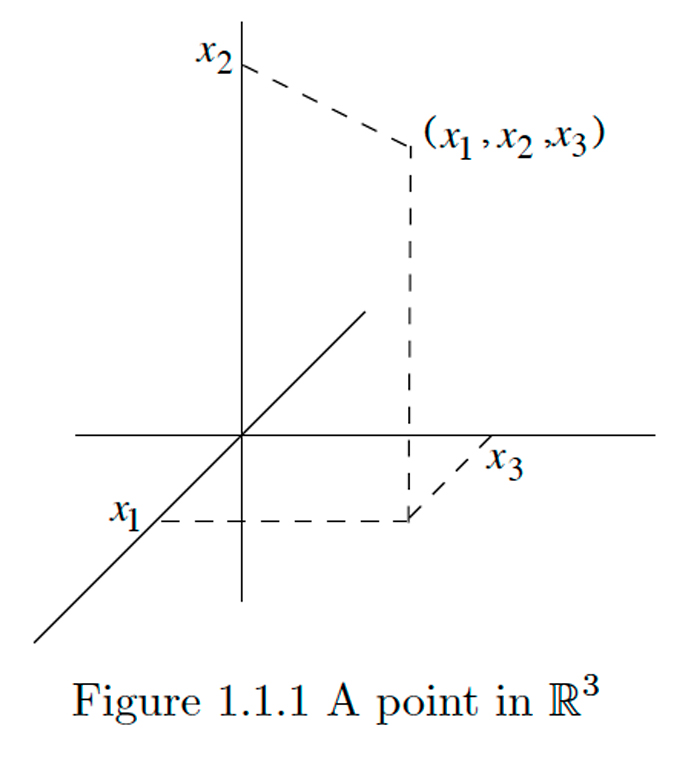
Es decir,\(\mathbb{R}^{n}\) es el espacio de todos los\(n\) ordenados-tuplas de números reales. Denotaremos un punto en este espacio por
\[\mathbf{x}=\left(x_{1}, x_{2}, \ldots, x_{n}\right),\]
y, pues\(i=1,2, \ldots, n,\) llamamos a\(x_{i}\) la coordenada\(i\) th de\(\mathbf{x}\).
Ejemplo\(\PageIndex{1}\)
Cuando\(n=2,\) tenemos
\[\mathbb{R}^{2}=\left\{\left(x_{1}, x_{2}\right): x_{1}, x_{2} \in \mathbb{R}\right\},\nonumber\]
que es nuestra representación familiar para los puntos en el plano cartesiano. Como es habitual, en este caso frecuentemente etiquetaremos las coordenadas como\(x\) y\(y,\) o algo similar, en lugar de numerarlas como\(x_{1}\) y\(x_{2}\).
Ejemplo\(\PageIndex{2}\)
Cuando\(n=3,\) tenemos
\[\mathrm{R}^{3}=\left\{\left(x_{1}, x_{2}, x_{3}\right): x_{1}, x_{2}, x_{3} \in \mathrm{R}\right\}.\nonumber\]
Así como podemos pensar en una forma de asignar coordenadas a puntos en el plano euclidiano, podemos pensar en asignar coordenadas al espacio euclidiano tridimensional.\(\mathbb{R}^{2}\)\(\mathbb{R}^{3}\) Para imaginar este espacio, debemos imaginar tres ejes mutuamente perpendiculares con las coordenadas marcadas a lo largo de los ejes como en la Figura\(1.1 .1 .\) Nuevamente, frecuentemente etiquetaremos las coordenadas de un punto en\(\mathbb{R}^{3}\) como, por ejemplo,\(x, y,\) y\(z,\) o\(u, v,\) y en\(w,\) lugar de usar coordenadas numeradas.
Ejemplo\(\PageIndex{3}\)
Si un objeto se mueve por el espacio, su ubicación puede especificarse con cuatro coordenadas, tres coordenadas espaciales, digamos,\(x, y,\)\(z,\) y una coordenada de tiempo, digamos\(t\) Así su ubicación es especificada por un punto\(\mathbf{p}=(x, y, z, t)\) en Por\(\mathbb{R}^{4} .\) supuesto, no podemos dibujar una imagen de tal punto.
Antes de comenzar nuestro estudio geométrico de primero\(\mathbb{R}^{n},\) necesitamos algunas definiciones algebraicas básicas.
Definición
Dejar\(\mathbf{x}=\left(x_{1}, x_{2}, \ldots, x_{n}\right)\) y\(\mathbf{y}=\left(y_{1}, y_{2}, \ldots, y_{n}\right)\) ser puntos adentro\(\mathbf{R}^{n}\) y dejar\(a\) ser un número real. Luego definimos
\[\mathbf{x}+\mathbf{y}=\left(x_{1}+y_{1}, x_{2}+y_{2}, \dots, x_{n}+y_{n}\right),\]
y
\[\mathbf{x}-\mathbf{y}=\left(x_{1}-y_{1}, x_{2}-y_{2}, \dots, x_{n}-y_{n}\right),\]
\[a \mathbf{x}=\left(a x_{1}, a x_{2}, \ldots, a x_{n}\right).\]
Ejemplo\(\PageIndex{4}\)
Si\(x=(2,-3,1)\) y\(y=(-4,1,-2)\) son dos puntos en\(R^{3},\) entonces
\[\begin{aligned} \mathbf{x}+\mathbf{y} &=(-2,-2,-1) \\ \mathbf{x}-\mathbf{y} &=(6,-4,3) \\ \mathbf{y}-\mathbf{x} &=(-6,4,-3) \\ 3 \mathbf{x} &=(6,-9,3), \end{aligned}\]
y
\[-2 y=(8,-2,4).\nonumber\]
Observe que definimos suma y resta para puntos en\(\mathbb{R}^{n},\) pero no definimos multiplicación. En general no existe ninguna forma de multiplicación para tales puntos que sea útil para nuestro propósito. Por supuesto, la multiplicación se define en el caso especial\(n=1\) y para el caso especial\(n=2\) si consideramos los puntos en\(\mathbb{R}^{2}\) como puntos en el plano complejo. Veremos en la Sección 1.3 que también existe un tipo interesante y útil de multiplicación en\(\mathbb{R}^{3} .\) También tenga en cuenta que\((1.1 .5)\) sí proporciona un método para multiplicar un punto en\(\mathbb{R}^{n}\) por un número real, siendo el resultado otro punto en\(\mathrm{R}^{n}\). En tales casos solemos referirnos al número real como escalar y a esta multiplicación como multiplicación escalar. En breve proporcionaremos una interpretación geométrica de esta forma de multiplicación.
Geometría de\(\mathbb{R}^{n}\)
Recordemos que si\(\mathbf{x}=\left(x_{1}, x_{2}\right)\) y\(\mathbf{y}=\left(y_{1}, y_{2}\right)\) son dos puntos en\(\mathbb{R}^{2},\) entonces, usando el teorema de Pitágoras, la distancia de\(\mathbf{x}\) a\(\mathbf{y}\) es
\[\sqrt{\left(y_{1}-x_{1}\right)^{2}+\left(y_{2}-x_{2}\right)^{2}}.\nonumber\]
Esta fórmula se generaliza fácilmente a\(\mathbb{R}^{3}:\) Supongamos\(\mathbf{x}=\left(x_{1}, x_{2}, x_{3}\right)\) y\(y=\left(y_{1}, y_{2}, y_{3}\right)\) son dos puntos en\(\mathrm{R}^{3} .\) Let\(\mathbf{z}=\left(y_{1}, y_{2}, x_{3}\right) .\) Dado que las dos primeras coordenadas de\(\mathbf{y}\) y\(\mathbf{z}\) son las mismas,\(\mathbf{y}\) y se\(\mathbf{z}\) encuentran en la misma línea vertical, y así la distancia entre ellas es simplemente
\[\left|y_{3}-x_{3}\right|.\]
Además,\(x\) y\(z\) tienen la misma tercera coordenada, y así se encuentran en el mismo plano horizontal. De ahí que la distancia entre\(\mathbf{x}\) y\(\mathbf{z}\) sea la misma que la distancia entre\(\left(x_{1}, x_{2}\right)\) y\(\left(y_{1}, y_{2}\right)\) en\(\mathbb{R}^{2},\) eso es,
\[\sqrt{\left(y_{1}-x_{1}\right)^{2}+\left(y_{2}-x_{2}\right)^{2}}.\nonumber\]
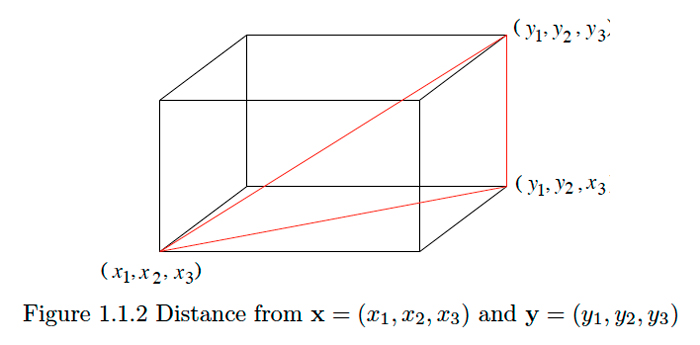
Finalmente, los puntos\(\mathbf{x}, \mathbf{y},\) y\(\mathbf{z}\) forman un triángulo rectángulo con ángulo recto en\(\mathbf{z} .\) Por lo tanto, utilizando de nuevo el teorema de Pitágoras, la distancia de\(x\) a\(y\) es
\[\sqrt{(\sqrt{\left(y_{1}-x_{1}\right)^{2}+\left(y_{2}-x_{2}\right)^{2}})^{2}+\left|y_{3}-x_{3}\right|^{2}}=\sqrt{\left(y_{1}-x_{1}\right)^{2}+\left(y_{2}-x_{2}\right)^{2}+\left(y_{3}-x_{3}\right)^{2}}.\nonumber\]
En particular, si dejamos\(\|x \|\) denotar la distancia desde\(x=\left(x_{1}, x_{2}, x_{3}\right)\) el origen\((0,0,0)\) en\(\mathbb{R}^{3},\) entonces
\[\|\mathbf{x}\|=\sqrt{x_{1}^{2}+x_{2}^{2}+x_{3}^{2}}.\nonumber\]
Con esta notación, la distancia de\(\mathbf{x}\) a\(\mathbf{y}\) es
\[\begin{aligned}\|\mathbf{y}-\mathbf{x}\| &=\left\|\left(y_{1}-x_{1}, y_{2}-x_{2}, y_{3}-x_{3}\right)\right\| \\ &=\sqrt{\left(y_{1}-x_{1}\right)^{2}+\left(y_{2}-x_{2}\right)^{2}+\left(y_{3}-x_{3}\right)^{2}} \end{aligned} \]
Ejemplo\(\PageIndex{5}\)
Si\(x=(1,2,-3)\) y\(y=(3,-2,1),\) entonces la distancia\(x\) desde el origen es
\[\|\mathbf{x}\|=\sqrt{1^{2}+2^{2}+(-3)^{2}}=\sqrt{14}\nonumber\]
y la distancia de\(x\) a\(y\) viene dada por
\[\|\mathbf{y}-\mathbf{x}\|=\|(2,-4,4)\|=\sqrt{4+16+16}=6.\nonumber\]
Aunque no tenemos analogías físicas con las que trabajar cuando,\(n>3,\) sin embargo, podemos generalizar\((1.1 .9)\) para definir la distancia en\(\mathbb{R}^{n}\).
Definición
Si\(x=\left(x_{1}, x_{2}, \ldots, x_{n}\right)\) es un punto en\(\mathbb{R}^{n},\) definimos la norma de\(x,\) denotado\(\|\mathbf{x}\|,\) por
\[\|\mathbf{x}\|=\sqrt{x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2}}.\nonumber\]
Para dos puntos\(\mathbf{x}\) y\(\mathbf{y}\) en\(\mathbb{R}^{n},\) definimos la distancia entre\(\mathbf{x}\) y\(\mathbf{y},\) denotado\(d(\mathbf{x}, \mathbf{y})\)
por
\[d(\mathbf{x}, \mathbf{y})=\|\mathbf{y}-\mathbf{x}\|.\nonumber\]
Vamos a dejar\(\mathbf{0}=(0,0, \ldots, 0)\) denotar el origen en\(\mathbb{R}^{n} .\) Entonces tenemos
\[\|\mathbf{x}\|=d(\mathbf{x}, \mathbf{0});\nonumber\]
es decir, la norma de\(x\) es la distancia desde\(x\) el origen.
Ejemplo\(\PageIndex{6}\)
Si\(x=(2,3,-1,5),\) un punto en\(\mathbb{R}^{4},\) entonces la distancia desde\(x\) el origen es
\[\|\mathbf{x}\|=\sqrt{4+9+1+25}=\sqrt{39}.\nonumber\]
Si\(\mathbf{y}=(3,2,1,4),\) entonces la distancia de\(\mathbf{x}\) a\(\mathbf{y}\) es
\[d(\mathbf{x}, \mathbf{y})=\|\mathbf{y}-\mathbf{x}\|=\|(1,-1,2,-1)\|=\sqrt{7}.\nonumber\]
Tenga en cuenta que si\(\mathbf{x}=\left(x_{1}, x_{2}, \ldots, x_{n}\right)\) es un punto en\(\mathbb{R}^{n}\) y\(a\) es un escalar, entonces
\[\begin{aligned} \|a \mathbf{x}\| &=\left\|\left(a x_{1}, a x_{2}, \ldots, a x_{n}\right)\right\| \\ &=\sqrt{a^{2} x_{1}^{2}+a^{2} x_{2}^{2}+\cdots+a^{2}x_{n}^{2}} \\ &=|a| \sqrt{x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2}} \\ &=|a|\|\mathbf{x}\|.\end{aligned}\]
Es decir, la norma de un múltiplo escalar de\(x\) es solo el valor absoluto del escalar multiplicado por la norma de\(\mathbf{x}\). En particular, si\(\mathbf{x} \neq \mathbf{0},\) entonces
\[\left\|\frac{1}{\|\mathbf{x}\|} \mathbf{x}\right\|=\frac{1}{\|\mathbf{x}\|}\|\mathbf{x}\|=1.\nonumber\]
Es decir,
\[\frac{1}{\|\mathbf{x}\|} \mathbf{x}\nonumber\]
es una unidad de distancia desde el origen.
Definición
Dejemos\(\mathbf{p}=\left(p_{1}, p_{2}, \ldots, p_{n}\right)\) ser un punto adentro\(\mathbb{R}^{n}\) y dejemos\(r>0\) ser un número real. El conjunto de todos los puntos\(\left(x_{1}, x_{2}, \ldots, x_{n}\right)\) en los\(\mathbb{R}^{n}\) que satisfacer la ecuación
\[\left(x_{1}-p_{1}\right)^{2}+\left(x_{2}-p_{2}\right)^{2}+\cdots+\left(x_{n}-p_{n}\right)^{2}=r^{2}\]
se llama esfera\((n-1)-\) dimensional con radio\(r\) y centro\(\mathbf{p},\) que denotamos\(S^{n-1}(\mathbf{p}, r) .\) El conjunto de todos los puntos\(\left(x_{1}, x_{2}, \ldots, x_{n}\right)\) en los\(\mathbb{R}^{n}\) que satisfacer la desigualdad
\[\left(x_{1}-p_{1}\right)^{2}+\left(x_{2}-p_{2}\right)^{2}+\cdots+\left(x_{n}-p_{n}\right)^{2}<r^{2}\]
se llama una bola abierta\(n\) -dimensional con radio\(r\) y centro\(\mathbf{p},\) que denotamos\(B^{n}(\mathbf{p}, r)\) El conjunto de todos los puntos\(\left(x_{1}, x_{2}, \ldots, x_{n}\right)\) en los\(\mathbb{R}^{n}\) que satisfacer la desigualdad
\[\left(x_{1}-p_{1}\right)^{2}+\left(x_{2}-p_{2}\right)^{2}+\cdots+\left(x_{n}-p_{n}\right)^{2} \leq r^{2}\]
se llama una bola n-dimensional cerrada con radio\(r\) y centro\(\mathbf{P},\) que denotamos\(\bar{B}^{n}(\mathbf{p}, r)\)
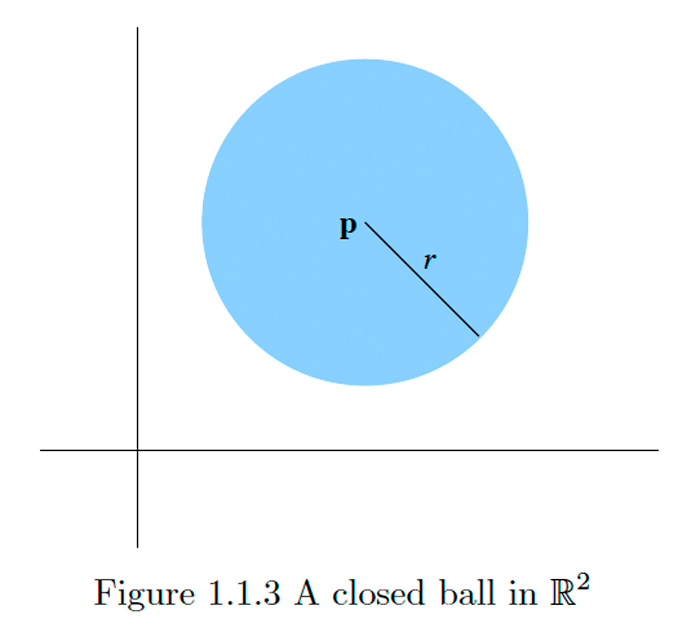
Una esfera\(S^{n-1}(\mathbf{p}, r)\) es el conjunto de todos los puntos que se encuentran a una distancia fija\(r\) desde un punto fijo\(\mathbf{p}\) en\(\mathbb{R}^{n}\). Tenga en cuenta que para\(n=1, S^{0}(\mathbf{p}, r)\) consta de sólo dos puntos, a saber, el punto\(\mathbf{p}-r\) que se encuentra\(r\) a una distancia a la izquierda de\(\mathbf{p}\) y el punto\(\mathbf{p}+r\) que se encuentra una distancia\(r\) a la derecha de\(\mathbf{p} ; B^{1}(\mathbf{p}, r)\) es el intervalo abierto\((\mathbf{p}-r, \mathbf{p}+r) ;\) y\(\bar{B}^{1}(\mathbf{p}, r)\) es el intervalo cerrado \([\mathbf{p}-r, \mathbf{p}+r] .\)En este sentido, las bolas abiertas y cerradas son análogos naturales de intervalos abiertos y cerrados en la línea real. Porque\(n=2,\) una esfera es un círculo, una bola abierta es un disco sin su círculo de cierre, y una bola cerrada es un disco junto con su círculo de cierre.
Vectores
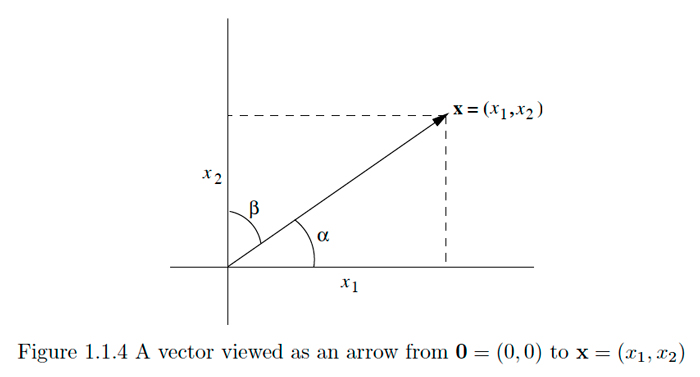
Muchas de las cantidades de interés en la física, como velocidades, aceleraciones y fuerzas, involucran tanto una magnitud como una dirección. Por ejemplo, podríamos hablar de una fuerza de magnitud 10 newtons que actúa sobre un objeto en el origen en un plano en ángulo\(\frac{\pi}{4}\) con la horizontal. Es común imaginar tal cantidad como una flecha, con longitud dada por la magnitud y con la punta apuntando en la dirección especificada, y referirse a ella como vector 8. Ahora cualquier punto\(\mathbf{x}=\left(x_{1}, x_{2}\right), \mathbf{x} \neq \mathbf{0},\) en\(\mathbb{R}^{2}\) especifica un vector en el plano, es decir, el vector que comienza en el origen y termina en\(\mathbf{x}\). La magnitud, o longitud, de dicho vector es\(\|\mathbf{x}\|\) y su dirección se especifica por el ángulo\(\alpha\) que hace con el eje horizontal o por el ángulo\(\beta\) que hace con el eje vertical. Tenga en cuenta que
\[\cos (\alpha)=\frac{x_{1}}{\|x\|}\nonumber\]
y
\[\cos (\beta)=\frac{x_{2}}{\|x\|}\nonumber\]
y que, aunque ni\(\cos (\alpha)\) ni de\(\cos (\beta)\) manera única determina la dirección del vector por sí mismo, juntos determinan completamente la dirección. Ver Figura 1.1.4.
En general, podemos pensar\(\mathbf{x}=\left(x_{1}, x_{2}, \ldots, x_{n}\right)\) ya sea como un punto en\(\mathbb{R}^{n}\) o como un vector en\(\mathbb{R}^{n},\) comenzar en el origen con longitud\(\|\mathbf{x}\| .\) Si\(\mathbf{x} \neq \mathbf{0},\) decimos, en analogía con el caso en
\(\mathrm{R}^{2},\)que la dirección de\(\mathrm{x}\) es el vector
\[\mathbf{u}=\left(\frac{x_{1}}{\|\mathbf{x}\|}, \frac{x_{2}}{\|\mathbf{x}\|}, \ldots, \frac{x_{n}}{\|\mathbf{x}\|}\right)\nonumber\]
Las coordenadas de este vector\(\mathbf{u}\) se llaman los cosenos de dirección\(\mathbf{x}\) porque podemos pensar en
\[u_{k}=\frac{x_{k}}{\|x\|} \nonumber\]
como el coseno del ángulo entre el vector\(x\) y el eje\(k\) th para\(k=1,2, \ldots, n,\) una interpretación que se hará más clara después de nuestra discusión de ángulos\(\mathbb{R}^{n}\) en la siguiente sección. Alternativamente, podemos pensar en un vector de longitud unitaria que apunta en la misma dirección que\(\mathbf{x}\).\(\mathbf{u}\) Cualquier vector de longitud\(1,\) tal como\(\mathbf{u},\) se llama vector de unidad. Llamamos\(\mathbf{0}\) al vector cero ya que tiene longitud 0. Tenga en cuenta que 0 no tiene dirección.
Ejemplo\(\PageIndex{7}\)
El vector\(\mathbf{x}=(1,2,-2,3)\) en\(\mathbf{R}^{4}\) tiene longitud\(\|\mathbf{x}\|=\sqrt{18}\) y dirección
\[\mathbf{u}=\left(\frac{1}{\sqrt{18}}, \frac{2}{\sqrt{18}},-\frac{2}{\sqrt{18}}, \frac{3}{\sqrt{18}}\right)=\frac{1}{\sqrt{18}}(1,2,-2,3)\nonumber\]
Ahora es posible dar significados geométricos a nuestras definiciones de multiplicación escalar, suma vectorial y resta vectorial. Primero tenga en cuenta que si\(\mathbf{x} \neq \mathbf{0}\) y\(a>0,\) luego
\[\|a \mathbf{x}\|=a\|\mathbf{x}\|,\nonumber\]
por lo que a\(\mathbf{x}\) tiene dirección
\[\frac{1}{\|a \mathbf{x}\|} a \mathbf{x}=\frac{1}{\|\mathbf{x}\|} \mathbf{x}\nonumber\]
lo mismo que\(\mathbf{x}\). Por lo tanto,\(a \mathbf{x}\) apunta en la misma dirección que\(\mathbf{x},\) pero con longitud\(a\) multiplicada por la longitud de\(\mathbf{x} .\) Si\(a<0,\) entonces
\[\|a \mathbf{x}\|=|a|\|\mathbf{x}\|=-a\|\mathbf{x}\|,\nonumber\]
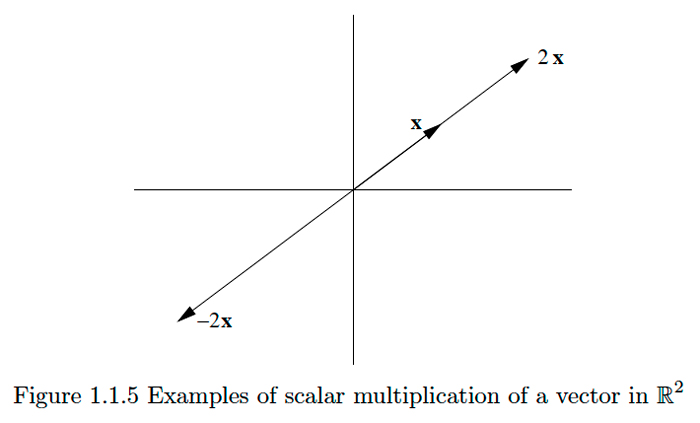
así\(a x\) tiene dirección
\[\frac{1}{\|a \mathbf{x}\|} a \mathbf{x}=-\frac{1}{\|\mathbf{x}\|} \mathbf{x}.\nonumber\]
De ahí que en este caso,\(a x\) tenga la dirección opuesta de\(x\) con\(|a|\) veces la longitud de x. Ver Figura 1.1.5 para ejemplos en\(\mathbb{R}^{2}\).
A continuación, considere dos vectores\(\mathbf{x}=\left(x_{1}, x_{2}\right)\) y\(\mathbf{y}=\left(y_{1}, y_{2}\right)\) en\(\mathbb{R}^{2}\) y su suma
\[\mathbf{z}=\mathbf{x}+\mathbf{y}=\left(x_{1}+y_{1}, x_{2}+y_{2}\right).\nonumber\]
Tenga en cuenta que la punta de\(\mathbf{z}\) se ubica\(x_{1}\) unidades horizontalmente y\(x_{2}\) unidades verticalmente desde la punta de\(\mathbf{y} .\) Geométricamente, la punta de\(\mathbf{z}\) está ubicada en la punta de\(\mathbf{x}\) si primero\(\mathbf{x}\) fueron trasladadas paralelas a sí mismas para que su cola ahora coincidiera con la punta de \(\mathbf{y} .\)Equivalentemente, podemos ver\(\mathbf{z}\) como la diagonal del paralelogramo que tiene\(\mathbf{x}\) y\(\mathbf{y}\) por sus lados. Véase la Figura 1.1.6 para un ejemplo.
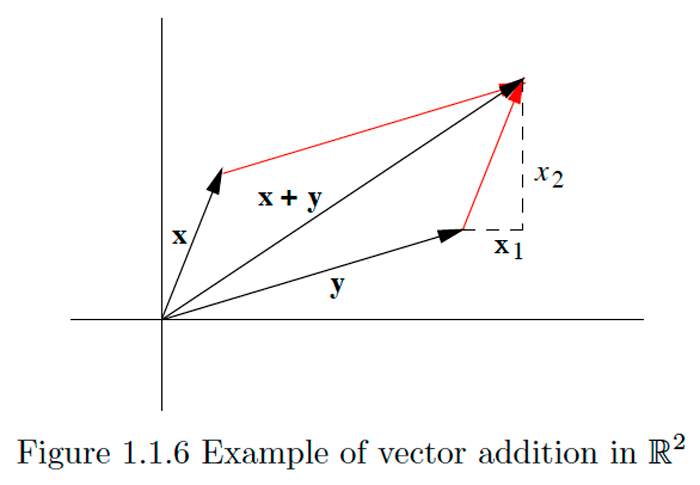
Por último, considere dos vectores\(\mathbf{x}=\left(x_{1}, x_{2}\right)\) y\(\mathbf{y}=\left(y_{1}, y_{2}\right)\) en\(\mathbb{R}^{2}\) y su diferencia
\[\mathbf{z}=\mathbf{x}-\mathbf{y}=\left(x_{1}-y_{1}, x_{2}-y_{2}\right).\]
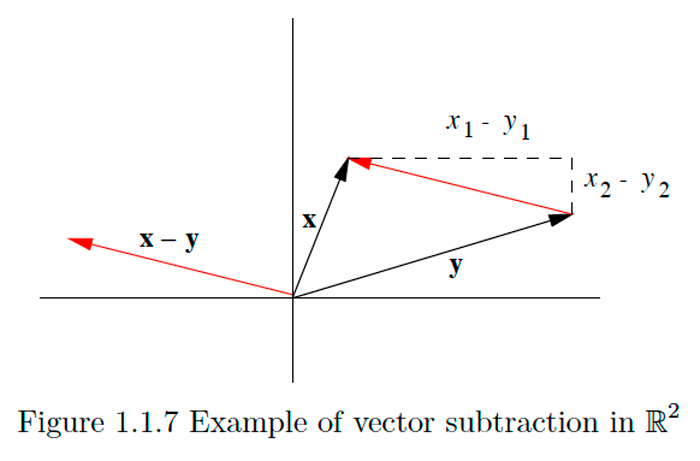
Tenga en cuenta que dado que las coordenadas de\(\mathbf{z}\) son solo las diferencias en las coordenadas de\(\mathbf{x}\) y\(\mathbf{y}\),\(\mathbf{z}\) tiene la magnitud y dirección de una flecha apuntando desde la punta de\(\mathbf{y}\) hasta la punta de\(\mathbf{x}\), como se ilustra en la Figura\(1.1 .7 .\) En otras palabras, podemos imaginar \(\mathbf{z}\)geométricamente trasladando una flecha dibujada desde la punta de\(\mathbf{y}\) hasta la punta de\(\mathbf{z}\) paralela a sí misma hasta que su cola esté en el origen.
En la discusión anterior es tentador pensar en la flecha desde la punta de\(\mathbf{y}\) hasta la punta de\(\mathbf{x}\) como realmente\(\mathbf{x}-\mathbf{y},\) no siendo solo un traductor paralelo de\(\mathbf{x}-\mathbf{y} .\) De hecho, es conveniente y útil pensar en traducciones paralelas de un vector dado, es decir, vectores que tienen la misma dirección y magnitud, pero con sus colas no en el origen, ya que todas siendo el mismo vector, simplemente dibujadas en diferentes lugares del espacio. Veremos muchas instancias en las que ver vectores de esta manera ayuda significativamente a nuestra comprensión.
Antes de cerrar esta sección, necesitamos llamar la atención sobre algunos vectores especiales.
Definición: Vectores de base estándar
Los vectores
\[\begin{array}{l}{\mathbf{e}_{1}=(1,0,0, \ldots, 0)} \\ {\mathbf{e}_{2}=(0,1,0, \ldots, 0)} \\ {\vdots} \\ {\mathbf{e}_{n}=(0,0,0, \ldots, 1)}\end{array}\]
in\(\mathbb{R}^{n}\) se llaman los vectores base estándar.
Ejemplo\(\PageIndex{8}\)
En\(\mathbb{R}^{2}\) los vectores base estándar son\(\mathbf{e}_{1}=(1,0)\) y\(\mathbf{e}_{2}=(0,1) .\) Tenga en cuenta que si\(\mathbf{x}=(x, y)\) hay algún vector en\(\mathbb{R}^{2},\) entonces
\[\mathbf{x}=(x, 0)+(0, y)=x(1,0)+y(0,1)=x \mathbf{e}_{1}+y e_{2}. \nonumber\]
Por ejemplo,\((2,5)=2 \mathrm{e}_{1}+5 \mathrm{e}_{2}\).
Ejemplo\(\PageIndex{9}\)
En\(\mathbb{R}^{3}\) los vectores base estándar son\(\mathrm{e}_{1}=(1,0,0), \mathrm{e}_{2}=(0,1,0),\) y\(\mathrm{e}_{3}=\)\((0,0,1) .\) Tenga en cuenta que si\(\mathbf{x}=(x, y, z)\) hay algún vector en\(\mathbb{R}^{3},\) entonces
\[\mathbf{x}=(x, 0,0)+(0, y, 0)+(0,0, z)=x(1,0,0)+y(0,1,0)+z(0,0,1)=x e_{1}+y e_{2}+z e_{3}\nonumber\]
Por ejemplo,\((1,2,-4)=\mathbf{e}_{1}+2 \mathbf{e}_{2}-4 \mathbf{e}_{3}\).
Los dos ejemplos anteriores se generalizan fácilmente para mostrar que cualquier vector en\(\mathrm{R}^{n}\) puede escribirse como una suma de múltiplos escalares de los vectores base estándar. Específicamente, si\(\mathbf{x}=\left(x_{1}, x_{2}, \ldots, x_{n}\right),\) entonces podemos escribir\(\mathbf{x}\) como
\[\mathbf{x}=x_{1} \mathbf{e}_{1}+x_{2} \mathbf{e}_{2}+\cdots+x_{n} \mathbf{e}_{n}.\]
Decimos que\(x\) es una combinación lineal de los vectores base estándar\(e_{1}, e_{2}, \ldots, e_{n} .\) También es importante señalar que solo hay una opción para los escalares en esta combinación lineal. Es decir, para cualquier vector\(\mathbf{x}\) en\(\mathbb{R}^{n}\) hay una y sólo una forma de escribir\(\mathbf{x}\) como una combinación lineal de los vectores base estándar.
Notas sobre notación
En este texto, denotaremos vectores usando una fuente sin formato en negrita. Esta es una convención común, pero no la única utilizada para denotar vectores. Otra convención de uso frecuente es colocar flechas por encima de una variable que denota un vector. Por ejemplo, uno podría escribir\(\vec{x}\) para lo que hemos estado denotando\(\mathbf{x}\).
También vale la pena señalar que en muchos libros los vectores base estándar en\(\mathbb{R}^{2}\) se denotan por i y\(\mathbf{j}(\text { or } \vec{i} \text { and } \vec{j}),\) y los vectores base estándar en\(\mathbb{R}^{3}\) por\(\mathbf{i}, \mathbf{j},\) y\(\mathbf{k}\) (o\(\vec{i}, \vec{j},\) y\(\vec{k}\)). Dado que esta notación no es fácil de extender a dimensiones superiores, no vamos a hacer mucho uso de ella.


