4.2: Condición de ángulo-lado-ángulo

Última actualización
Guardar como PDF

Page ID: 114604

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Teorema$\PageIndex{1}$ ASA condition

Supongamos que

$AB = A'B'$,$\measuredangle ABC = \pm \measuredangle A'B'C'$,$\measuredangle CAB = \pm \measuredangle C'A'B'$

y no$\triangle A'B'C'$ es degenerado. Entonces

$\triangle ABC \cong \triangle A'B'C'$.

Tenga en cuenta que para los triángulos degenerados la sentencia no se sostiene. Por ejemplo, considere un triángulo con lados 1, 4, 5 y el otro con lados 2, 3, 5.

Prueba

Según el Teorema 3.3.1, ya sea

\[\begin{array} {l} {\meausredangle ABC = \measuredangle A'B'C',} \\ {\measuredangle CAB = \measuredangle C'A'B'} \end{array}\]

\[\begin{array} {l} {\meausredangle ABC = -\measuredangle A'B'C',} \\ {\measuredangle CAB = -\measuredangle C'A'B'.} \end{array}\]

Además suponemos que 4.2.1 sostiene; el caso 4.2.2 es análogo.

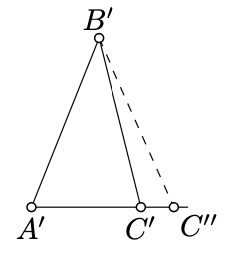
$2021-02-03 10.47.15.png$

Que$C''$ sea el punto en la media línea$[A'C')$ tal que$A'C'' = AC$.

Por Axioma IV,$\triangle A'B'C'' \cong \triangle ABC$. Aplicando de nuevo Axioma IV, lo conseguimos

$\measuredangle A'B'C'' = \measuredangle ABC = \measuredangle A'B'C'$.

Por Axioma IIIa,$[B'C') = [BC'')$. De ahí que$C''$ miente tanto$(B'C')$ como en$(A'C')$.

Ya que no$\triangle A'B'C'$ es degenerado,$(A'C')$ es distinto de$(B'C')$. Aplicando Axioma II, lo conseguimos$C'' = C'$.

Por lo tanto,$\triangle A'B'C' = \triangle A'B'C'' \cong \triangle ABC$.