4.5: En ángulo lateral y ángulo lateral

Última actualización
Guardar como PDF

Page ID: 114629

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En cada una de las condiciones SAS, ASA y SSS especificamos tres partes correspondientes de los triángulos. Hablemos de otras triples de las partes correspondientes.

El triple puño se llama ángulo lateral, o brevemente SSA; especifica dos lados y un ángulo no incluido. Esta condición no es suficiente para la congruencia; es decir, hay dos triángulos no degenerados$ABC$ y$A'B'C'$ tales que

$AB = A'B',$$BC = B'C'$,$\measuredangle BAC \equiv \pm \measuredangle B'A'C'$,

sino$\triangle ABC \not\cong \triangle A'B'C'$ y además$AC \ne A'C'$.

No vamos a utilizar esta afirmación negativa en la secuela y por lo tanto no hay necesidad de probarla formalmente. Un ejemplo se puede adivinar a partir del diagrama.

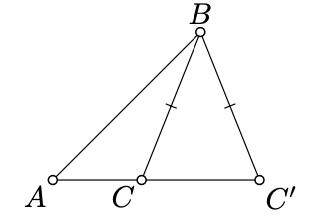
$2021-02-03 4.11.09.png$

El segundo triple es ángulo lateral, o brevemente SAA; especifica un lado y dos ángulos uno de los cuales es opuesto al lado. Esto proporciona una condición de congruencia; es decir, si uno de los triángulos$ABC$ o$A'B'C'$ es no degenerado y$AB = A'B'$$\measuredangle ABC \equiv \pm \measuredangle A'B'C'$,$\measuredangle BCA \equiv \pm \measuredangle B'C'A'$, entonces$\triangle ABC \cong \triangle A'B'C'$.

La condición SAA no se utilizará directamente en la secuela. Una prueba de esta condición se puede obtener de ASA y el teorema sobre la suma de ángulos de un triángulo probado a continuación (ver Teorema 7.4.1). Para una prueba más directa, véase Ejercicio 11.1.2.

Otro triple se llama ángulo-ángulo-ángulo, o brevemente AAA; por el Axioma V, no es una condición de congruencia en el plano euclidiano, sino en el plano hiperbólico lo es; ver Teorema 13.3.2.