4.4: Condición Lado Lateral
- Page ID
- 114618
\(\triangle ABC \cong \triangle A'B'C'\)si
\(A'B' = AB\),\(B'C' = BC\) y\(C'A' = CA\).
Tenga en cuenta que esta condición también es válida para triángulos degenerados.
- Prueba
-
Elige\(C''\) para que\(A'C'' = A'C'\) y\(\measuredangle B'A'C'' = \measuredangle BAC\). Según Axioma IV,
\(\triangle A'B'C'' \cong \triangle ABC.\)
Baste con demostrar que
\[\triangle A'B'C' \cong \triangle A'B'C''.\]
La condición 4.4.1 se mantiene trivialmente si\(C'' = C'\). Por lo tanto, queda por considerar el caso\(C'' \ne C'\).
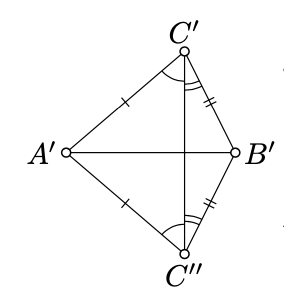
Claramente, los lados correspondientes de\(\triangle A'B'C'\) y\(\triangle A'B'C''\) son iguales. De ahí los triángulos\(\trianggle C'A'C''\) y\(\triangle C'B'C''\) son isósceles. Por Teorema 4.3.1, tenemos
\(\begin{array} {l} {\measuredangle A'C''C' \equiv -\measuredangle A'C'C''} \\ {\measuredangle C'C''B' \equiv -\measuredangle C''C'B'.} \end{array}\)
Agregándolos, obtenemos
\(\measuredangle A'C''B' \equiv -\measuredangle A'C'B'.\)
Aplicando de nuevo Axioma IV, obtenemos 4.4.1
Si\(AB + BC = AC\), entonces\(B \in [AC]\).
- Prueba
-
Podemos suponer que\(AB > 0\) y\(BC > 0\); de otra manera\(A = B\) o\(B = C\).
Argumentar por contradicción, supongamos\(AB + BC = AC\). Elija\(B' \in [AC]\) tal que\(AB = AB'\); tenga en cuenta que\(BC = B'C\) y\(\measuredangle AB'C = \pi\).
Por\(SSS\),
\(\triangle ABC \cong \triangle AB'C.\)
Por lo tanto\(\measuredangle ABC = \pi\). Por teorema 2.4.1,\(B\) yace entre\(A\) y\(C\).
Dejar\(M\) ser el punto medio del lado\([AB]\) de\(\triangle ABC\) y\(M'\) ser el punto medio del lado\([A'B']\) de\(\triangle A'B'C'\). Supongamos\(C'A' = CA\)\(C'B' = CB\),, y\(C'M' = CM\). Demostrar que
\(\triangle A'B'C' \cong \triangle ABC\).
- Sugerencia
-
Considerar los puntos\(D\) y\(D'\), tal que\(M\) es el punto medio de\([CD]\) y\(M'\) es el punto medio de\([C'D']\). Demuéstralo\(\triangle BCD \cong \triangle B'C'D'\) y úsalo para probarlo\(\triangle A'B'C' \cong \triangle ABC\).
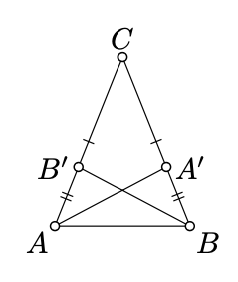
Dejar\(\triangle ABC\) ser un triángulo isósceles con la base\([AB]\). Supongamos que\(CA' = CB'\) para algunos puntos\(A' \in [BC]\) y\(B' \in [AC]\). Demostrar que
a)\(\triangle AA'C \cong \triangle BB'C\);
b)\(\triangle ABB' \cong \triangle BAA'\).
- Sugerencia
-
(a) Aplicar SAS.
b) Utilizar (a) y aplicar SSS.
Dejar\(\triangle ABC\) ser un triángulo no degenerado y dejar\(f\) ser un movimiento del plano tal que
\(f(A) = A\),\(f(B) = B\) y\(f(C) = C\).
Mostrar que\(f\) es el mapa de identidad; es decir,\(f(X) = X\) para cualquier punto\(X\) del plano.
- Sugerencia
-
Sin pérdida de general, podemos suponer que\(X\) es distinto de\(A, B,\) y\(C\). Establecer\(f(X) = X'\); asumir\(X' \ne X\).
Tenga en cuenta que\(AX = AX'\)\(BX = BX'\),, y\(CX = CX'\). Por SSS lo conseguimos\(\angle ABX = \pm \measuredangle ABX'\). Ya que\(X \ne X'\), lo conseguimos\(\measuredangle ABX \equiv - \measuredangle ABX'\). De la misma manera que lo conseguimos\(\measuredangle CBX \equiv -\measuredangle CBX'\). Restando estas dos identidades la una de la otra, eso lo conseguimos\(\measuredangle ABC \equiv - \measuredangle ABC\). Concluir que\(\measuredangle ABC = 0\) o\(\pi\). Es decir,\(\triangle ABC\) es degenerado —una contradicción.


