6.4: La desigualdad de Tolomeo

Última actualización
Guardar como PDF

Page ID: 114368

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Un cuadrilátero se define como un cuádruple ordenado de puntos distintos en el plano. Estos 4 puntos se denominan vértices de cuadrilátero. El cuadrilátero ABCD también será denotado por$\square ABCD$.

Dado un cuadrilátero$ABCD$, los cuatro segmentos$[AB]$$[BC]$$[CD]$,,, y$[DA]$ se llaman lados de$\square ABCD$; los dos segmentos restantes$[AC]$ y$[BD]$ se llaman diagonales de$\square ABCD$.

Teorema$\PageIndex{1}$ Ptolemy's inequality

En cualquier cuadrilátero, el producto de las diagonales no puede exceder la suma de los productos de sus lados opuestos; es decir,

\[AC \cdot BD \le AB \cdot CD + BC \cdot DA\]

para cualquier$\square ABCD$.

Presentaremos una prueba clásica de esta desigualdad utilizando el método de triángulos similares con una construcción adicional. Esta prueba se da como ilustración — no se utilizará más en la secuela.

Prueba

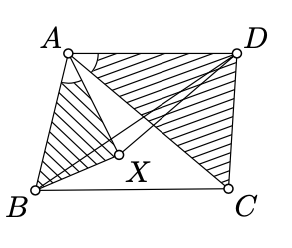
$2021-02-09 9.05.34.png$

Considera la media línea$[AX)$ tal que$\measuredangle BAX = \measuredangle CAD$. En este caso$\measuredangle XAD = \measuredangle BAC$ ya que la adición$\measuredangle BAX$ o$\measuredangle CAD$ a los lados correspondientes produce$\measuredangle BAD$. Podemos suponer que

$AX = \dfrac{AB}{AC} \cdot AD.$

En este caso tenemos

$\dfrac{AX}{AD} = \dfrac{AB}{AC}$,$\dfrac{AX}{AB} = \dfrac{AD}{AC}.$

De ahí

$\triangle BAX \sim \triangle CAD$,$\triangle XAD \sim \triangle BAC$.

Por lo tanto,

$\dfrac{BX}{CD} = \dfrac{AB}{AC}$,$\dfrac{XD}{BC} = \dfrac{AD}{AC}.$

o, equivalentemente

$AC \cdot BX = AB \cdot CD$,$AC \cdot XD = BC \cdot AD$.

Sumando estas dos igualdades obtenemos

$AC \cdot (BX + XD) = AB \cdot CD + BC \cdot AD$.

Queda por aplicar el triángulo de desigualdad,$BD \le BX + XD$.

Utilizando la prueba anterior junto con el Corolario 9.3.2, se puede demostrar que la igualdad se mantiene sólo si los vértices$A, B, C$, y$D$ aparecen en una línea o un círculo en el mismo orden cíclico; véase también Teorema 10.4.1 para otra prueba del caso de igualdad. El ejercicio 18.3.2 a continuación sugiere otra prueba de la desigualdad de Tolomeo usando coordenadas complejas.