6.3: Método de triángulos similares

Última actualización
Guardar como PDF

Page ID: 114367

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

La prueba del teorema de Pitágoras dada anteriormente utiliza el método de triángulos similares. Para aplicar este método, hay que buscar pares de triángulos similares y luego usar la proporcionalidad de lados correspondientes y/o igualdades de ángulos correspondientes. Encontrar tales parejas podría ser complicado al principio.

Ejercicio$\PageIndex{1}$

Dejar$ABC$ ser un triángulo no degenerado y los puntos$X, Y$, y$Z$ como en el diagrama. Asumir$\measuredangle CAY \equiv \measuredangle XBC$. Encuentra cuatro pares de triángulos similares con estos seis puntos como los vértices y demuestra su similitud.

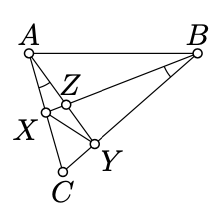
$2021-02-08 1.39.11.png$

Pista

Por la condición de similitud AA (Teorema 6.1.2),$\triangle AYC \sim \triangle BXC$. Concluir eso$\dfrac{YC}{AC} = \dfrac{XC}{BC}$. Aplicar la condición de similitud SAS para demostrarlo$\triangle ABC \sim \triangle YXC$.

De igual manera, aplicar AA e igualdad de ángulos verticales para demostrarlo$\triangle AZX \sim \triangle BZY$ y usar SAS para demostrarlo$\triangle ABZ \sim \triangle YXZ$.