9.6: Medias líneas tangentes

Última actualización
Guardar como PDF

Page ID: 114814

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Supongamos que$ABC$ es un arco de círculo$\Gamma$. Una media línea$[AX)$ se llama tangente al arco$ABC$ en$A$ si la línea$(AX)$ es tangente a$\Gamma$, y los puntos$X$ y se$B$ encuentran en el mismo lado de la línea$(AC)$.

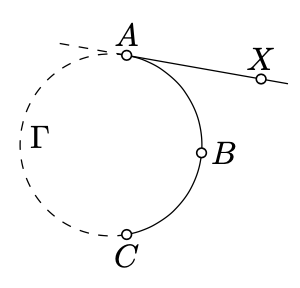
$2021-02-19 9.44.12.png$

Si el arco está formado por el segmento de línea$[AC]$, entonces la media línea$[AC)$ se considera tangente en$A$. Si el arco está formado por una unión de dos medias líneas$[AX)$ y$[BY)$ adentro$(AC)$, entonces la media línea$[AX)$ se considera tangente al arco en$A$.

Proposición$\PageIndex{1}$

La media línea$[AX)$ es tangente al arco$ABC$ si y solo si

$\measuredangle ABC + \measuredangle CAX \equiv \pi$.

Prueba

Para un arco degenerado$ABC$, la afirmación es evidente. Además asumimos que el arco no$ABC$ es degenerado.

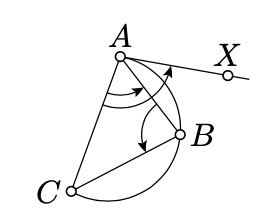
$2021-02-19 9.46.58.png$

Aplicando el Teorema 9.1.1 y el Teorema 9.2.1, obtenemos que

$2 \cdot \measuredangle ABC + 2 \cdot \measuredangle CAX \equiv 0$.

Por lo tanto, ya sea

$\measuredangle ABC + \measuredangle CAX \equiv \pi$, o$\measuredangle ABC + \measuredangle CAX \equiv 0$.

Ya que$[AX)$ es la tangente media línea al arco$ABC, X$ y$B$ se encuentran en el mismo lado de$(AC)$. Por Corolario 3.4.1 y Teorema 3.3.1, los ángulos$CAX$,$CAB$, y$ABC$ tienen el mismo signo. En particular,$\measuredangle ABC + \measuredangle CAX \not\equiv 0$; es decir, nos quedamos con el caso

$\measuredangle ABC +\measuredangle CAX \equiv \pi$.

Ejercicio$\PageIndex{1}$

Mostrar que hay un arco único con puntos finales en los puntos dados$A$ y$C$, que es tangente a la media línea dada$[AX)$ en$A$.

Pista

Si$C \in (AX)$, entonces el arco es el segmento de línea$[AC]$ o la unión de dos medias líneas$(AX)$ con vértices en$A$ y$C$.

Asumir$C \not\in (AX)$. Dejar$\ell$ ser la línea perpendicular caída de$A$ a$(AX)$ y$m$ ser la bisectriz perpendicular de$[AC]$.

Tenga en cuenta que$\ell \nparallel m$; establecer$O = \ell \cap m$. Tenga en cuenta que el círculo con centro que$O$ pasa a través también$A$ está pasando a través$C$ y tangente a$(AX)$.

Tenga en cuenta que uno de los dos arcos con puntos finales$A$ y$C$ es tangente a$[AX)$.

La singularidad se desprende de la Proposición$\PageIndex{1}$.

Ejercicio$\PageIndex{2}$

Dejar$[AX)$ ser la media línea tangente a un arco$ABC$. Supongamos que$Y$ es un punto en el arco$ABC$ que es distinto de$A$. $\measuredangle XAY \to 0$Demuéstralo como$AY \to 0$.

Pista: Usa Proposición$\PageIndex{1}$ y Teorema 7.4.1 para demostrarlo$\measuredangle XAY = \measuredangle ACY$. Por Axioma IIIc,$\measuredangle ACY \to 0$ como$AY \to 0$; de ahí el resultado.

Ejercicio$\PageIndex{3}$

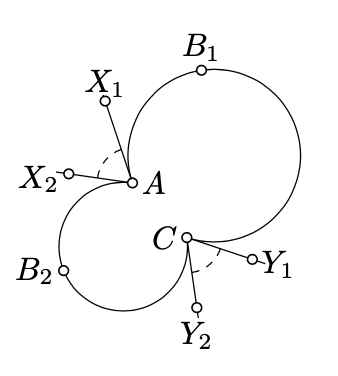
Dados dos arcos de círculo$AB_1C$ y$AB_2C$, dejar$[AX_1)$ y$[AX_2)$ en$A$,$[CY_1)$ y$[CY_2)$ ser las medias líneas tangentes a los arcos$AB_1C$ y$AB_2C$ en$C$. Demostrar que

$\measuredangle X_1AX_2 \equiv -\measuredangle Y_1CY_2.$

$2021-02-19 9.56.08.png$

Pista

Aplicar Proposición$\PageIndex{1}$ dos veces.

(Alternativamente, aplicar Corolario 5.4.1 para la reflexión a través de la bisectriz perpendicular de$[AC]$.)

Proposición\(\PageIndex{1}\)

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)

Ejercicio\(\PageIndex{3}\)