9.5: Arcos de circlinos

Última actualización
Guardar como PDF

Page ID: 114813

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Un subconjunto de un círculo delimitado por dos puntos se denomina arco circular.

Más precisamente, supongamos que$A, B, C$ son puntos distintos en un círculo$\Gamma$. El arco circular$ABC$ es el subconjunto que incluye los puntos así$A, C$ como todos los puntos en los$\Gamma$ que se encuentran$B$ en el mismo lado de$(AC)$.

Para el arco circular$ABC$, los puntos$A$ y$C$ se denominan puntos finales. Precisamente hay dos arcos de círculo de$\Gamma$ con los extremos dados; son opuestos entre sí.

Supongamos$X$ ser otro punto sobre$\Gamma$. Por Corolario 9.3.2 tenemos eso$2 \cdot \measuredangle AXC \equiv 2 \cdot \measuredangle ABC$; es decir,

$\measuredangle AXC \equiv \measuredangle ABC$o$\measuredangle AXC \equiv \measuredangle ABC + \pi.$

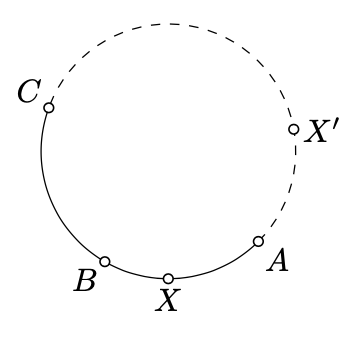
$2021-02-19 9.13.18.png$

Recordemos eso$X$ y$B$ acuéstese del mismo lado de$(AC)$ si y solo si$\angle AXC$ y$\angle ABC$ tienen el mismo signo (ver Ejercicio 3.4.2). De ello se deduce que

$X$yace en el arco$ABC$ si y solo si

$\measuredangle AXC \equiv \measuredangle ABC$;

$X$se encuentra en el arco opuesto a$ABC$ si

$\measuredangle AXC \equiv \measuredangle ABC + \pi$.

Tenga en cuenta que$ABC$ se define un arco circular si no$\triangle ABC$ está degenerado. Si$\triangle ABC$ es degenerado, entonces arco$ABC$ se define como un subconjunto de línea delimitada por$A$ y$C$ que contienen$B$.

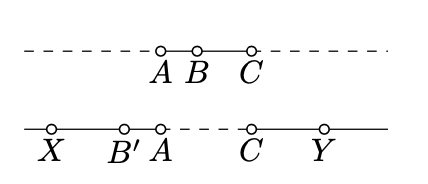
$2021-02-19 9.15.46.png$

Más precisamente, si$B$ se encuentra entre$A$ y$C$, entonces el arco$ABC$ se define como el segmento de línea$[AC]$. Si$B'$ se encuentra en la extensión de$[AC]$, entonces el arco$AB'C$ se define como una unión de medias líneas disjuntas$[AX)$ y$[CY)$ en$(AC)$. En este caso los arcos$ABC$ y$AB'C$ se llaman opuestos entre sí.

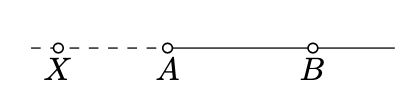
$2021-02-19 9.17.46.png$

Además, cualquier media línea$[AB)$ será considerada como un arco. Si$A$ se encuentra entre$B$ y$X$, entonces se$[AX)$ llamará oppostie a$[AB)$. Este arco degenerado tiene solo un punto final$A$.

Será conveniente utilizar la noción de circlina, que significa círculo o línea. Por ejemplo, cualquier arco es un subconjunto de una circlina; también podemos usar el término arco circlino si queremos hacer hincapié en que el arco podría estar degenerado. Tenga en cuenta que para cualquier tres puntos distintos$A, B$, y$C$ hay un arco circlino único$ABC$.

En la siguiente declaración se resume la discusión anterior.

Proposición$\PageIndex{1}$

Dejar$ABC$ ser un arco circlino y$X$ ser un punto distinto de$A$ y$C$. Entonces

(a)$X$ se encuentra en el arco$ABC$ si y sólo si

$\measuredangle AXC = \measuredangle ABC;$

(b)$X$ se encuentra en el arco opuesto a$ABC$ si y solo si

$\measuredangle AXC \equiv \measuredangle ABC + \pi$;

Ejercicio$\PageIndex{1}$

Ante un triángulo agudo$ABC$ hacer una construcción brújula y gobernante del punto de$Z$ tal manera que

$\measuredangle AZB = \measuredangle BZC = \measuredangle CZA = \pm \dfrac{2}{3} \cdot \pi$

Pista

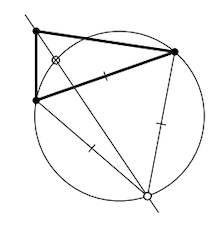
$2021-02-19 2.40.25.png$

Adivina una construcción a partir del diagrama. Para demostrar que produce el punto necesario, aplicar el Teorema 9.2.1.

Ejercicio$\PageIndex{2}$

Supongamos que ese punto$P$ se encuentra en el circuncírculo de un triángulo equilátero$ABC$ y$PA \le PB \le PC$. $PA + PB = PC$Demuéstralo.

Pista

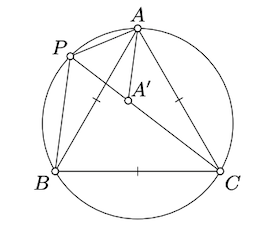
$2021-02-19 9.36.37.png$

Demostrar que$P$ se encuentra en el arco opuesto a$ACB$; concluir que$\measuredangle APC = \measuredangle CPB = \pm \dfrac{\pi}{3}$.

Elige un punto$A' \in [PC]$ tal que$PA' = PA$. Tenga en cuenta que$\triangle APA'$ es equilátero. Demostrar y usar eso$\triangle AA'C \cong \triangle APB.$

$ABCD$Se inscribe un cuadrángulo si todos los puntos$A, B, C$, y se$D$ encuentran sobre una circlina$\Gamma$. Si los arcos$ABC$ y$ADC$ son opuestos, entonces decimos que los puntos$A, B, C$, y$D$ aparecen$\Gamma$ en el mismo orden cíclico.

Esta definición permite formular el siguiente refinamiento del Corolario 9.3.2 que incluye los cuadrangulares degenerados. Se desprende directamente de la Proposición$\PageIndex{1}$.

Proposición$\PageIndex{2}$

Un cuadriángulo$ABCD$ se inscribe en una circlina si y solo si

$\measuredangle ABC = \measuredangle ADC$o$\measuredangle ABC \equiv \measuredangle ADC + \pi.$

Además, la segunda identidad se mantiene si y sólo si los puntos$A,B,C,D$ aparecen en la circlina en el mismo orden cíclico.

Proposición\(\PageIndex{1}\)

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)

Proposición\(\PageIndex{2}\)