13.1: Ángulo de paralelismo

Última actualización
Guardar como PDF

Page ID: 114341

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Deja$P$ ser un punto fuera de una línea h$\ell$. Deja caer una perpendicular$(PQ)_h$ de$P$ a$\ell$; deja$Q$ ser su punto de pie. $\phi$Sea el valor más pequeño tal que la línea h$(PZ)_h$ con$|\measuredangle_h Q P Z|=\phi$ no se intersecte$\ell$.

El valor$\phi$ se llama el ángulo de paralelismo de$P$ a$\ell$. Claramente,$\phi$ depende sólo de la distancia h$s=PQ_h$. Además,$\phi(s) \to \pi/2$ como$s \to 0$, y$\phi(s) \to 0$ como$s \to \infty$. (En la geometría euclidiana, el ángulo de paralelismo es idénticamente igual a$\pi/2$.)

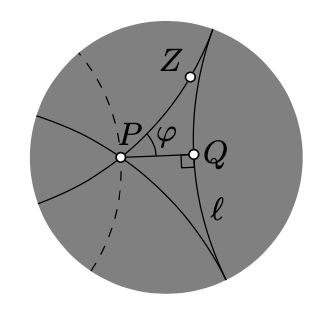
$2021-02-24 2.07.43.png$

Si$\ell$,$P$, y$Z$ son como arriba, entonces la línea h$m=(PZ)_h$ se llama asintóticamente paralela a$\ell$. Es decir, dos líneas h son asintóticamente paralelas si comparten un punto ideal. (En geometría hiperbólica, el término líneas paralelas se usa a menudo para líneas asintóticamente paralelas; no seguimos esta convención).

Dado$P \not\in \ell$, hay exactamente dos líneas asintóticamente paralelas$P$ a través de a$\ell$; las líneas paralelas restantes se llaman ultra paralelas.

En el diagrama, las dos líneas h continuas que pasan a través$P$ son asintóticamente paralelas a$\ell$; la línea h discontinua es ultra paralela a$\ell$.

Ejercicio$\PageIndex{1}$

Mostrar que dos líneas h distintas$\ell$ y$m$ son ultraparallel si y sólo si tienen una perpendicular común; es decir, hay una$h$ -línea$n$ tal que$n \perp \ell$ y$n \perp m$.

Pista

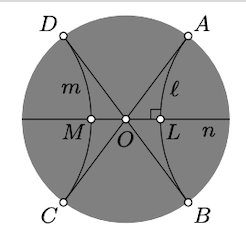
$2021-02-24 2.24.54.png$

“solo si” parte. Supongamos$\ell$ y$m$ son ultraparallel; es decir, no se cruzan y tienen distintos puntos ideales. Denotar los puntos ideales por$A, B, C$, y$D$; podemos suponer que aparecen en lo absoluto en el mismo orden. En este caso la línea h con puntos ideales$A$ y$C$ cruza la línea h con puntos ideales$B$ y$D$. Denote por$O$ su punto de intersección.

Por Lema 12.3.1, podemos suponer que$O$ es el centro de lo absoluto. Nótese que$\ell$ es el reflejo de$m$ lo ancho$O$ en el sentido euclidiano. Suelta una perpendicular h$n$ de$O$ a$\ell$, y muéstralo$n \perp m$.

“Si” parte. Supongamos que$n$ es una perpendicular común. Denote por$L$ y$M$ sus puntos de intersección con$\ell$ y$m$ respectivamente. Por Lema 12.3.1, podemos suponer que el centro de absoluto$O$ es el punto medio h de$L$ y$M$. Obsérvese que en este caso$\ell$ es el reflejo de m a través$O$ en el sentido euclidiano. De ello se deduce que los puntos ideales de las líneas h$\ell$ y$m$ son simétricos entre sí. Por lo tanto, si un par de ellos coincide, entonces también lo es el otro par. Por el Ejercicio 12.1.1,$\ell = m$, que contradice el supuesto$\ell \ne m$.

Proposición$\PageIndex{1}$

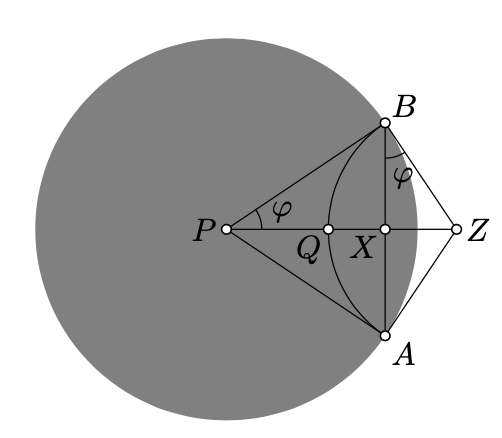
Deja$Q$ ser el punto del pie de$P$ en h-line$\ell$. Entonces

$PQ_h=\dfrac{1}{2} \cdot \ln \dfrac{1 + \cos \phi}{1 - \cos \phi},$

donde$\phi$ está el ángulo de paralelismo de$P$ a$\ell$.

En particular, si$P \notin \ell$ y$\beta =|\measuredangle_h XPY|$ por algunos puntos$X,Y\in\ell$, entonces

$PQ_h < \dfrac{1}{2} \cdot \ln \dfrac{1+\cos \dfrac{\beta}{2}}{1- \cos \dfrac{\beta}{2}}.$

$2021-02-24 2.16.20.png$

Prueba

Aplicando un movimiento del plano h si es necesario, podemos suponer que$P$ es el centro de lo absoluto. Entonces las líneas h a través$P$ son las intersecciones de las líneas euclidianas con el plano h.

Dejar$A$ y$B$ denotar los puntos ideales de$\ell$. Sin pérdida de generalidad, podemos suponer que eso$\angle APB$ es positivo. En este caso

$\phi=\measuredangle QPB=\measuredangle APQ=\dfrac{1}{2} \cdot\measuredangle APB.$

Dejar$Z$ ser el centro del círculo$\Gamma$ que contiene la línea h$\ell$. Establecer$X$ para ser el punto de intersección del segmento euclidiano$[AB]$ y la línea$(PQ)$.

Tenga en cuenta que,$PX = \cos \phi$. Por lo tanto, por Lemma 12.3.2,

$PX_h=\ln \dfrac{1+\cos\phi}{1-\cos\phi}.$

Tenga en cuenta que ambos ángulos$PBZ$ y$BXZ$ son rectos. Dado que el ángulo$PZB$ es compartido,$\triangle ZBX \sim \triangle ZPB$. En particular,

$ZX \cdot ZP = ZB^2;\]$

es decir,$X$ es la inversa de$P$ in$\Gamma$.

La inversión en$\Gamma$ es el reflejo del plano h a través$\ell$. Por lo tanto

$\begin{array} {rcl} {PQ_h} & = & {QX_h =} \\ {} & = & {\dfrac{1}{2} \cdot PX_h =} \\ {} & = & {\dfrac{1}{2} \cdot \ln \dfrac{1 + \cos \phi}{1 - \cos \phi}.} \end{array}$

La última declaración sigue since$\phi > \dfrac{\beta}{2}$ y la función

está disminuyendo en el intervalo$(0,\dfrac{\pi}{2}]$.

Ejercicio$\PageIndex{2}$

Dejar$ABC$ ser un triángulo h equilátero con lado$100$. Demostrar que

$|\measuredangle_h ABC|<\frac1{10\ 000\ 000\ 000}.$

Pista: Por desigualdad triangular, la distancia h de$B$ a$(AC)_h$ es de al menos 50. Queda por estimar$|\measuredangle_h ABC| using Proposition \(\PageIndex{1}$. Las desigualdades$\cos \phi \le 1 - \dfrac{1}{10} \cdot \phi^2$ para$|\phi| < \dfrac{\pi}{2}$ y$e^3 > 10$ deberían ayudar a terminar la prueba.

Ejercicio\(\PageIndex{1}\)

Proposición\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)