13.2: Inradio del triángulo h

Última actualización
Guardar como PDF

Page ID: 114326

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Teorema$\PageIndex{1}$

El inradio de cualquier triángulo h es menor que$\dfrac{1}{2} \cdot \ln3$.

Prueba

Dejar$I$ y$r$ ser el h-incenter y h-inradius de$\triangle_hXYZ$.

Tenga en cuenta que los ángulos h$XIY$,$YIZ$ y$ZIX$ tienen el mismo signo. Sin pérdida de generalidad, podemos suponer que todos ellos son positivos y por lo tanto

$\measuredangle_hXIY+ \measuredangle_hYIZ+ \measuredangle_hZIX=2 \cdot \pi$

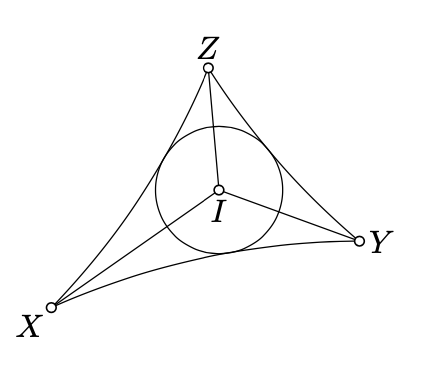
$2021-02-24 3.30.51.png$

Podemos suponer que$\measuredangle_hXIY \ge \dfrac{2}{3} \cdot \pi$; si no relabel$X$,$Y$, y$Z$.

Dado que$r$ es la distancia h de$I$ a$(XY)_h$, la Proposición 13.1.1 implica que

$\begin{array} {rcl} {r} & < & {\dfrac{1}{2} \cdot \ln \dfrac{1 + \cos \dfrac{\pi}{3}}{1 - \cos \dfrac{\pi}{3}}} \\ {} & = & {\dfrac{1}{2} \cdot \ln \dfrac{1 + \dfrac{1}{2}}{1 - \dfrac{1}{2}}} \\ {} & = & {\dfrac{1}{2} \cdot \ln 3.} \end{array}$

Ejercicio$\PageIndex{1}$

Dejar$\square_h ABCD$ ser un cuadriángulo en el plano h tal que los ángulos h en$A$,$B$, y$C$ son correctos y$AB_h=BC_h$. Encuentra el límite superior óptimo para$AB_h$.

Insinuación

Tenga en cuenta que el ángulo de prarllelismo de$B$ a$(CD)_h$ es mayor que$\dfrac{\pi}{4}$, y converge a$\dfrac{\pi}{4}$ como$CD_h \to \infty$.

Aplicando la Proposición 13.1.1, obtenemos que

$BC_h < \dfrac{1}{2} \cdot \ln \dfrac{1 + \dfrac{1}{\sqrt{2}}}{1 - \dfrac{1}{\sqrt{2}}} = \ln (1 + \sqrt{2}).$

El lado derecho es el límite de$BC_h$ si$CD_h \to \infty$. Por lo tanto,$\ln (1 + \sqrt{2})$ es el límite superior óptimo.