14.1: Transformaciones afín
- Page ID
- 114672
La geometría afín estudia la denominada estructura de incidencia del plano euclidiano. La estructura de incidencia ve solo qué puntos se encuentran sobre qué líneas y nada más; no ve directamente distancias, medidas de ángulo, y muchas otras cosas.
Una biyección del plano euclidiano a sí misma se denomina transformación afín si mapea líneas a líneas; es decir, la imagen de cualquier línea es una línea. Entonces podemos decir que la geometría afín estudia las propiedades del plano euclidiano conservadas bajo transformaciones afín.
Mostrar que una transformación afín del plano euclidiano envía cualquier par de líneas paralelas a un par de líneas paralelas.
- Pista
-
Asumir las dos líneas distintas\(\ell\) y\(m\) se mapean a las líneas de intersección\(\ell'\) y\(m'\). Supongamos que\(P'\) denota su punto de intersección.
Dejar\(P\) ser la imagen inversa de\(P'\). Por la definición de mapa afín, tiene que mentir sobre ambos\(\ell\) y\(m\); es decir,\(\ell\) y\(m\) se cruzan. De ahí el resultado.
La siguiente observación sigue ya que las líneas se definen utilizando únicamente la métrica.
Cualquier movimiento del plano euclidiano es una transformación afín.
El siguiente ejercicio proporciona ejemplos más generales de transformaciones afín.
Los siguientes mapas de un plano de coordenadas a sí mismo son transformaciones afín:
(a) Mapa de cizallamiento definido por\((x,y) \mapsto (x + k \cdot y, y)\) para una constante\(k\).
(b) Escalado definido por\((x, y) \mapsto (a \cdot x, a \cdot y)\) para una constante\(a \ne 0\).
(c)\(x\) -escalado y\(y\) -escalado definidos respectivamente por
\((x, y) \mapsto (a \cdot x, y)\), y\((x, y) \mapsto (x, a \cdot y)\)
para una constante\(a \ne 0\).
d) Una transformación definida por
\((x, y) \mapsto (a \cdot x + b \cdot y + r, c \cdot x + d \cdot y + s)\)
para constantes\(a, b, c, d, r, z\) tales que la matriz\(\begin{matrix} a & b \\ c & d \end{matrix}\) sea invertible.
- Pista
-
En cada caso verifique que el mapa sea una biyección y aplique el Ejercicio 7.6.3
Del teorema fundamental de la geometría afín (Teorema 14.3.1), se deduce que cualquier transformación afín puede escribirse en la forma (d).
Recordemos que los puntos son colineales si se encuentran en una línea.
Supongamos que\(P\mapsto P'\) es una biyección del plano euclidiano que mapea triples colineales de puntos a triples colineales. Mostrar que\(P\mapsto P'\) mapea triples no colineales a no colineales.
Concluir que\(P\mapsto P'\) es una transformación afín.
- Pista
-
Elige una línea\((AB)\).
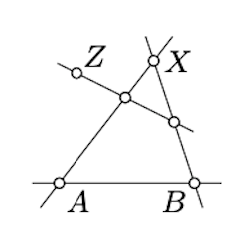
Supongamos que\(X' \in (A'B')\) para algunos\(X \not\in (AB)\). Dado que los\(P \mapsto P'\) mapas de colliner apuntan a colineales, las tres líneas\((AB), (AX)\), y\((BX)\) se mapean a\((A'B')\). Además, también se mapea a cualquier línea que conecte un par de puntos en estas tres líneas\((A'B')\). Utilízala para mostrar que todo el plano está mapeado\((A'B')\). Esto último contradice que el mapa es una biyección.
Por suposición, si\(X \in (AB)\), entonces\(X' \in (A'B')\). Forma por encima de lo contrario sostiene también. Utilízala para acreditar la segunda declaración.


