1.6: Ciasificaciones de Triángulo
- Page ID
- 114567
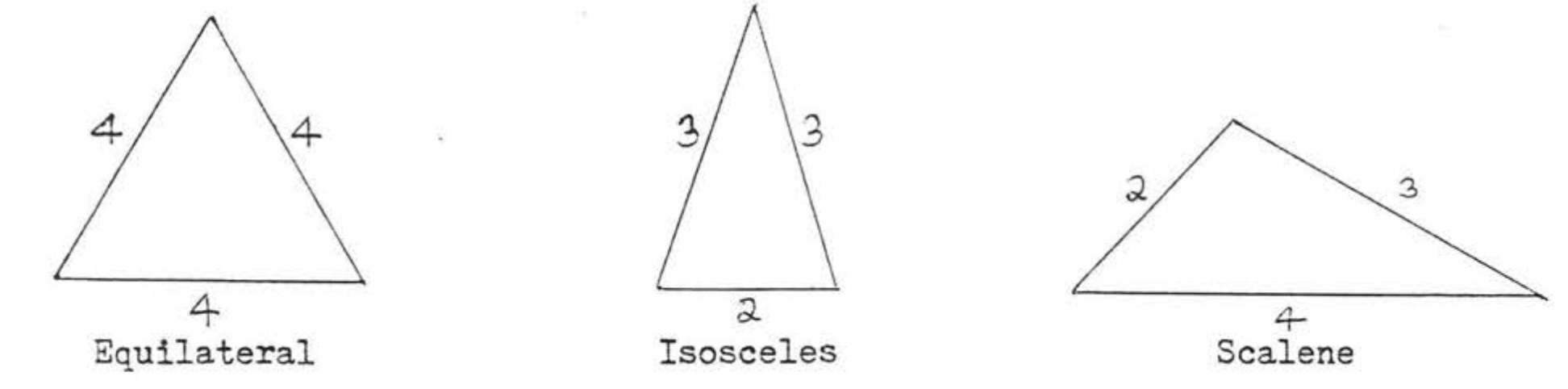
Los triángulos pueden clasificarse según las longitudes relativas de sus lados:
- Un triángulo equilátero tiene tres lados iguales,
- Un triángulo isósceles tiene dos lados iguales.
- Un triángulo escaleno no tiene lados iguales.
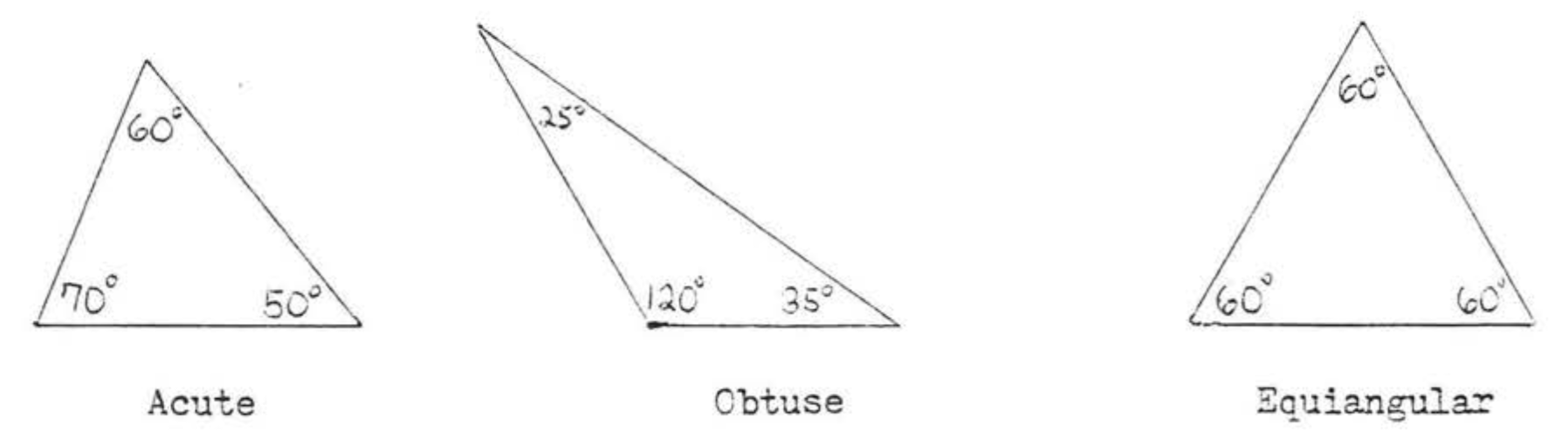
Los triángulos también pueden clasificarse según la medida de sus ángulos:
- Un triángulo agudo es un triángulo con tres ángulos agudos.
- Un triángulo obtuso es un triángulo con un ángulo obtuso.
- Un triángulo equiangular es un triángulo con tres ángulos iguales,
Cada ángulo de un triángulo equiangular debe ser\(60^{\circ}\), Mostraremos en la sección 2, 5 que los triángulos equiangulares son los mismos que los triángulos equiláteros,
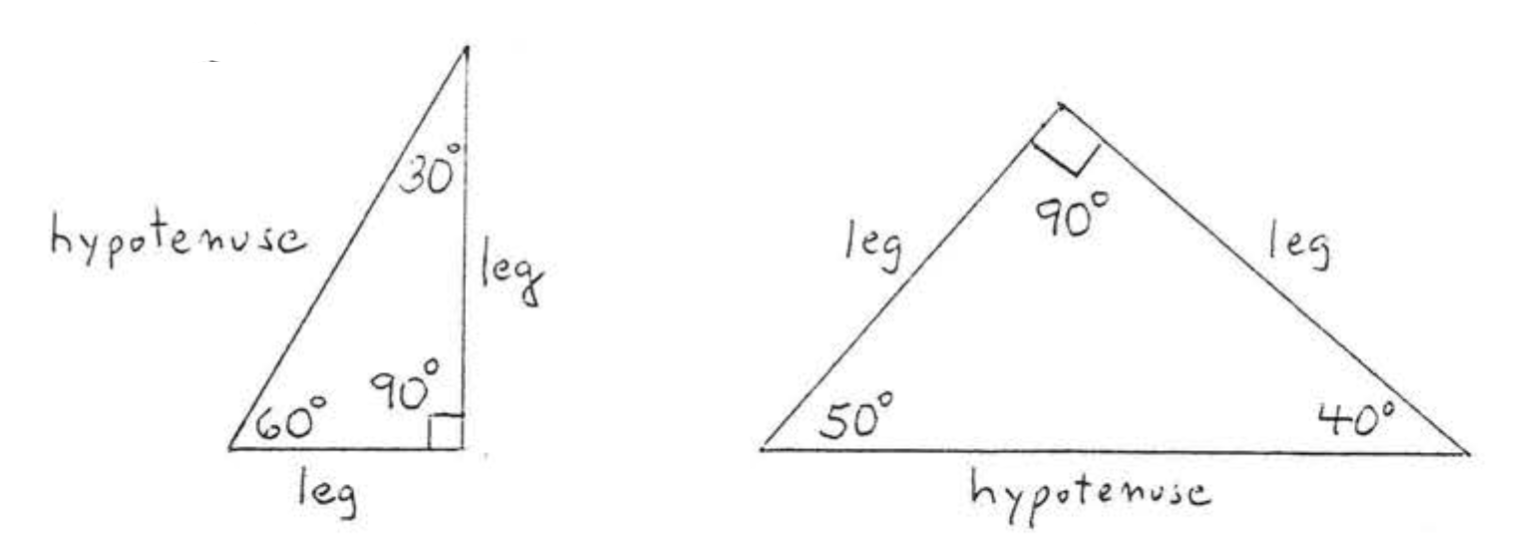
Un triángulo rectángulo es un triángulo con un ángulo recto, Los lados del ángulo recto se llaman las patas del triángulo y el lado restante se llama hipotenusa,
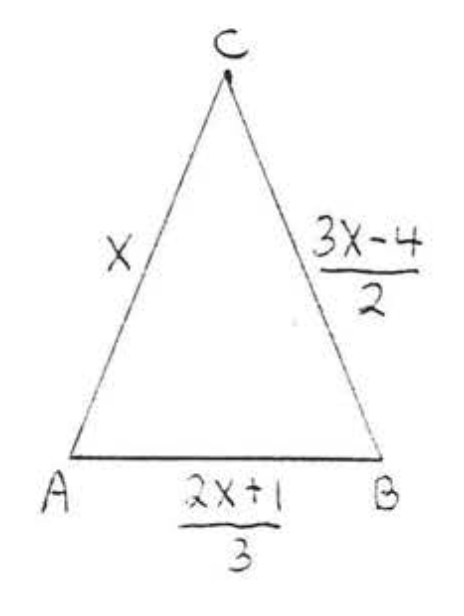
Encuentra\(x\) si\(\triangle ABC\) es isósceles con\(AC = BC\):
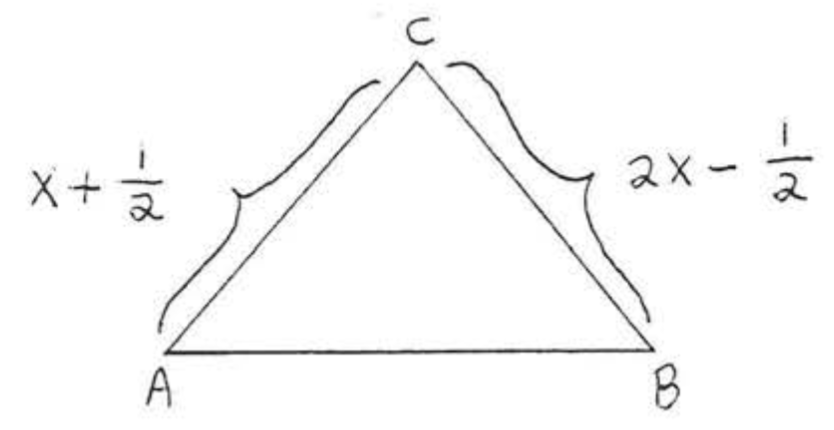
Solución
\[\begin{array} {rcl} {x + \dfrac{1}{2}} & = & {2x - \dfrac{1}{2}} \\ {(2)(x + \dfrac{1}{2})} & = & {(2) (2x - \dfrac{1}{2})} \\ {2x + 2 (\dfrac{1}{2})} & = & {(2)(2x) - (2) (\dfrac{1}{2})} \\ {2x + 1} & = & {4x - 1} \\ {1 + 1} & = & {4x - 2x} \\ {2} & = & {2x} \\ {1} & = & {x} \end{array}\]
Comprobar:
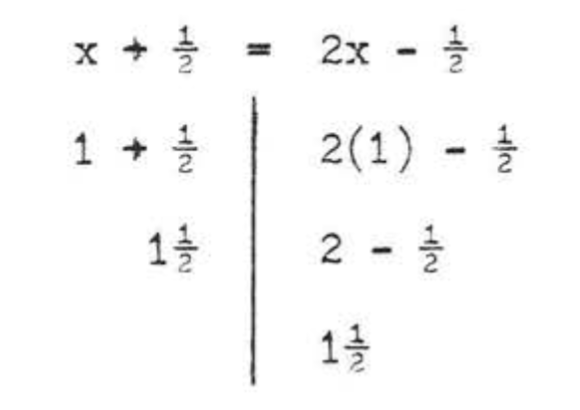
Respuesta:\(x = 1\).
\(\triangle ABC\)es equilátero. Encuentra\(x\):
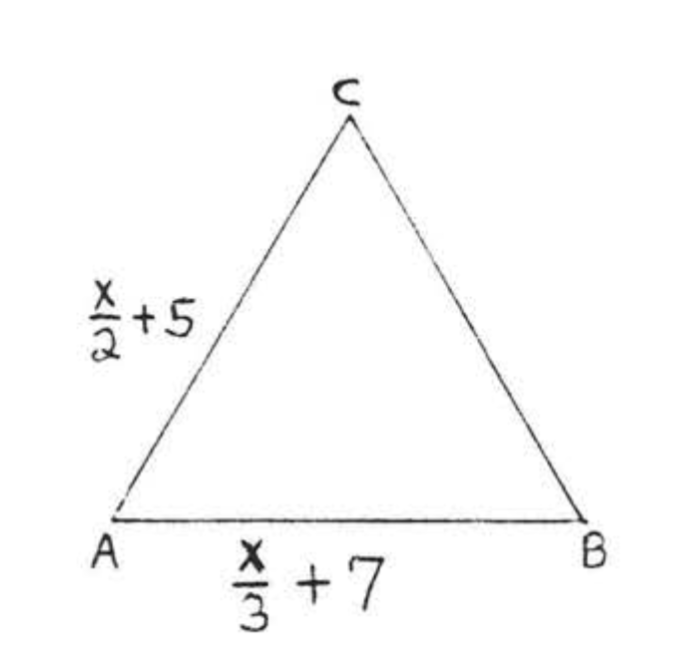
Solución
\[\begin{array} {rcl} {\dfrac{x}{2} + 5} & = & {\dfrac{x}{3} + 7} \\ {(6)(\dfrac{x}{2} + 5)} & = & {(6) (\dfrac{x}{3} + 7)} \\ {(6) (\dfrac{x}{2} + (6)(5)} & = & {(6)(\dfrac{x}{3} + (6)(7)} \\ {3x + 30} & = & {2x + 42} \\ {3x - 2x} & = & {42 - 30} \\ {x} & = & {12} \end{array}\]
Comprobar:

Respuesta:\(x = 12\).
Una altitud de un triángulo es un segmento de línea desde un vértice perpendicular al o·lado, En la Figura 4,\(CD\) y\(GH\) son altitudes, Tenga en cuenta que la altitud\(GH\) se encuentra afuera\(\triangle EFG\) y el lado\(EF\) debe extenderse para encontrarla.
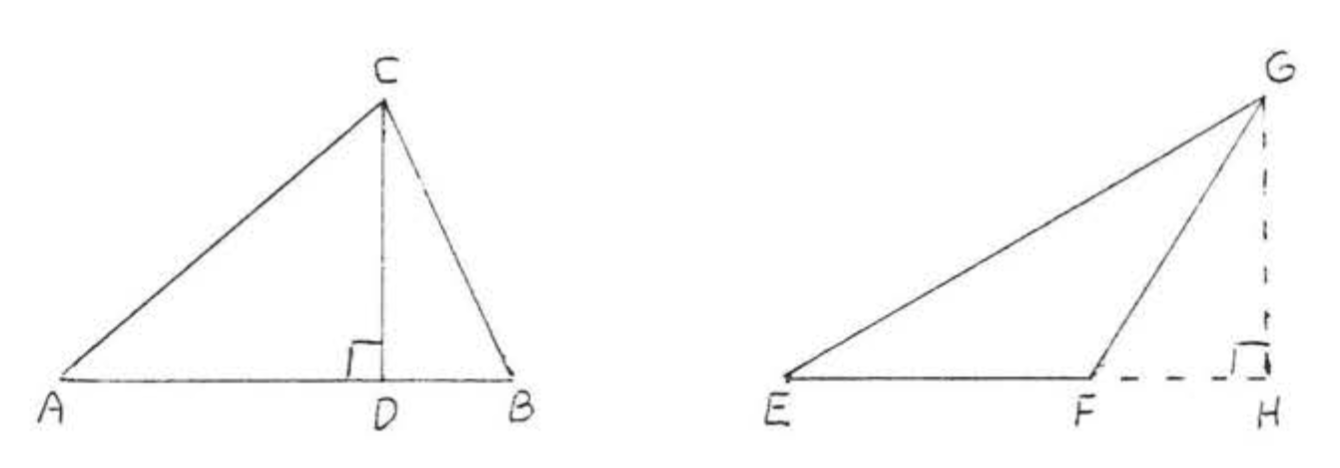
Una mediana de un triángulo es un segmento de línea desde un vértice hasta el punto medio del lado opuesto, En la Figura 5, CD es una mediana,
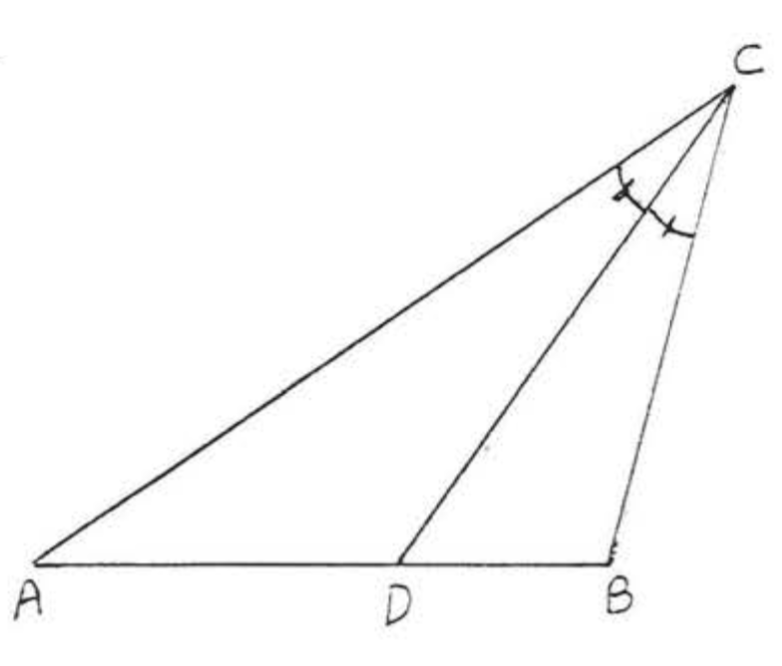
Un ángulo bisectriz es un rayo que divide un ángulo en dos ángulos eauales. En la Figura\(\PageIndex{6}\), \(\overrightarrow{CD}\) is an angle bisector.
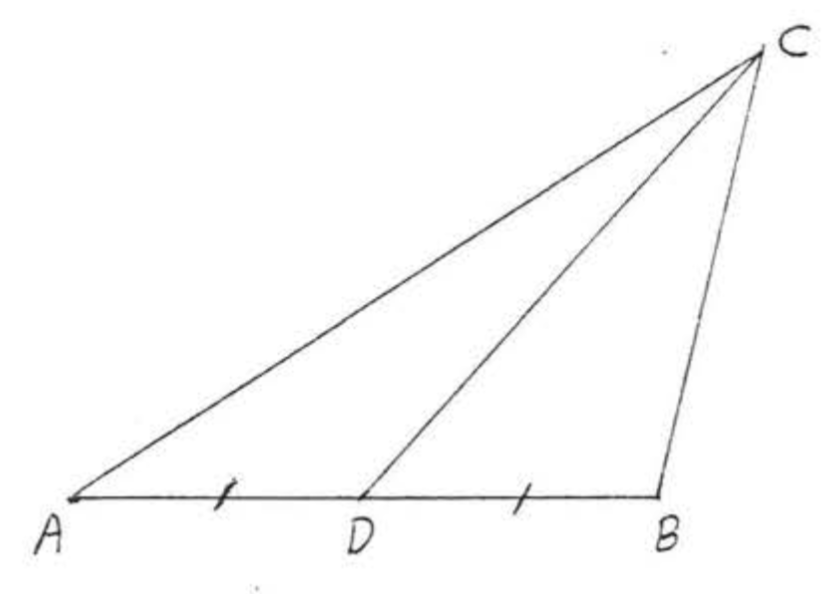
\(AB\)Averiguar si\(CD\) es una mediana:
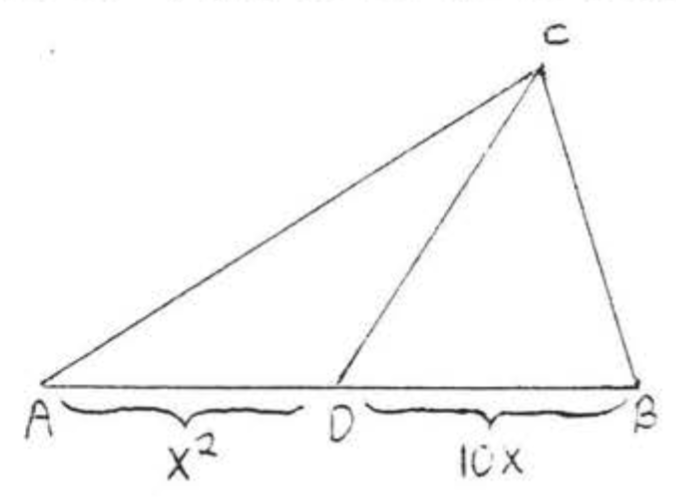
Solución
\[\begin{array} {rcl} {AD} & = & {DB} \\ {x^2} & = & {10x} \\ {x^2 - 10x} & = & {0} \\ {(x)(x - 10)} & = & {0} \end{array}\]
\(\begin{array} {rclcrcl} {x} & = & {0} & \text{ or } & {x - 10} & = & {0} \\ {} & & {} & \text{ } & {x} & = & {10} \end{array}\)
Comprobar,\(x = 0\):
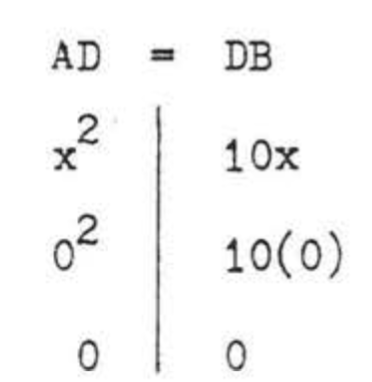
Comprobar,\(x = 10\):
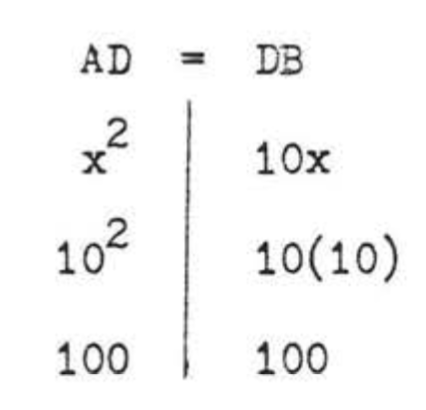
Rechazamos la respuesta\(x = 0\) porque la longitud de un segmento de línea debe ser mayor que 0, Por lo tanto\(AB = AD + DB = 100 + 100 = 200\).
Respuesta:\(AB = 200\).
Encuentra\(\angle ACB\) si\(\overrightarrow{CD}\) es un ángulo bisectriz:
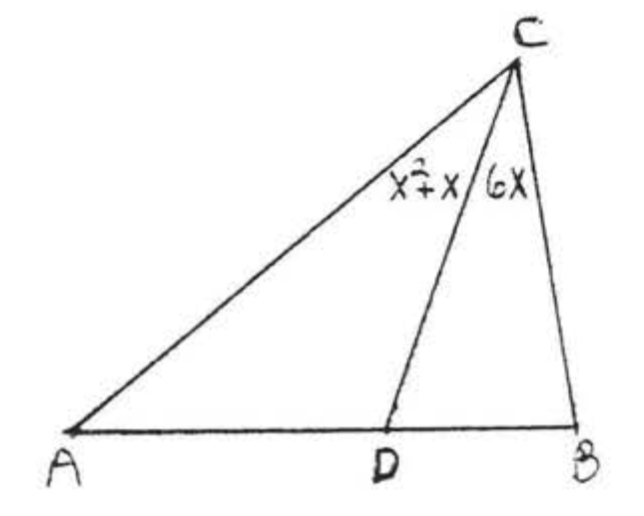
Solución
\[\begin{array} {rcl} {\anlge ACD} & = & {\angle BCD} \\ {x^2 + x} & = & {6x} \\ {x^2 + x - 6x} & = & {0} \\ {x^2 - 5x} & = & {0} \\ {(x)(x - 5)} & = & {0} \end{array}\]
\(\begin{array} {rclcrcl} {x} & = & {0} & \text{ or } & {x - 5} & = & {0} \\ {} & & {} & \text{ } & {x} & = & {5} \end{array}\)
Comprobar,\(x = 0\):
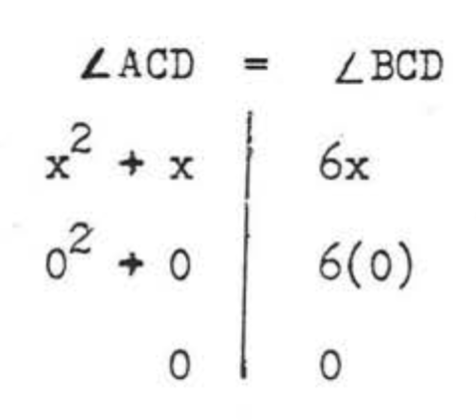
Comprobar,\(x = 5\):

Rechazamos la respuesta\(x = 0\) porque las medidas de\(\angle ACD\) y\(\angle BCD\) deben ser mayores que\(0^{\circ}\). Por lo tanto\(\angle ACB = \angle ACD + \angle BCD = 30^{\circ} + 30^{\circ} = 60^{\circ}\).
Respuesta:\(\angle ACB = 60^{\circ}\).
El perímetro de un triángulo es la suma de las longitudes de los lados. El perímetro de\(\triangle ABC\) en la Figura\(\PageIndex{7}\) is \(3 + 4 + 5 = 12\).
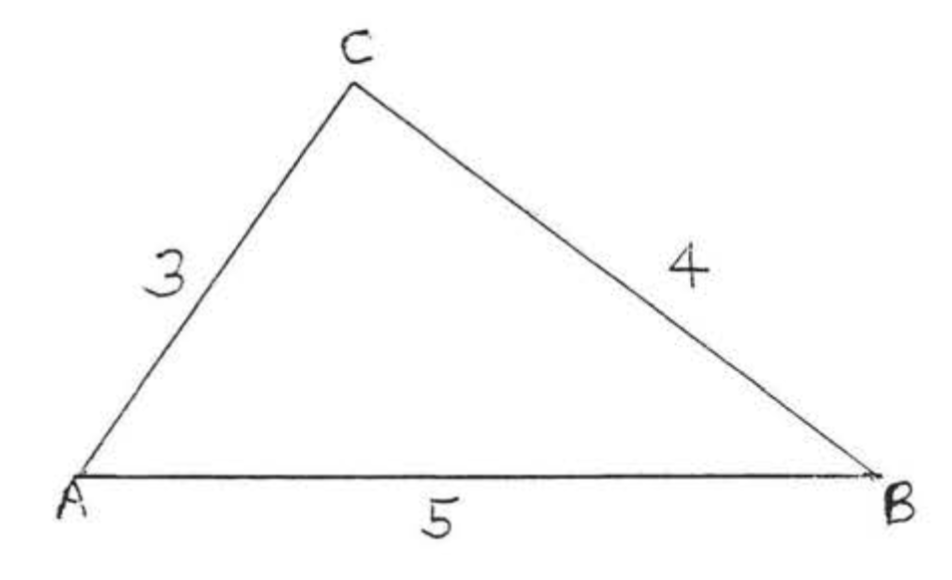
La suma de cualquiera de los dos lados de un triángulo es mayor que el lado restante.
Por ejemplo, en la Figura\(\PageIndex{7}\), \(AC + BC = 3 + 4 > AB = 5\).
- Prueba
-
Esto se deduce del postulado de que la distancia más corta entre dos nointas es a lo largo de una línea recta, Por ejemplo\(\PageIndex{7}\), en la Figura, la longitud\(AB\) (un segmento de línea recta) debe ser menor que las longitudes combinadas de\(AC\) y\(CB\) (no en una línea recta de\(A\) a \(B\)),
Encuentra el perímetro del triángulo en términos de\(x\), Luego encuentra el perímetro si\(x = 1\):
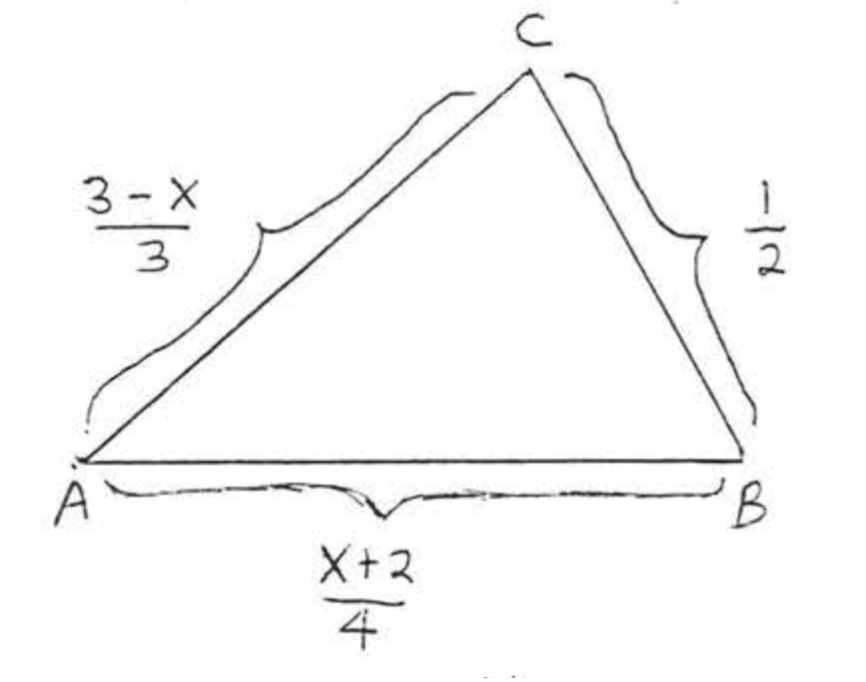
Solución
\[\begin{array} {rcl} {} & = & {} \\ {} & = & {} \\ {} & = & {} \\ {} & = & {} \\ {} & = & {} \end{array}\]
Si\(x = 1\),\(\dfrac{24 - x}{12} = \dfrac{24 - 1}{12} = \dfrac{23}{12}\).
Comprobar:
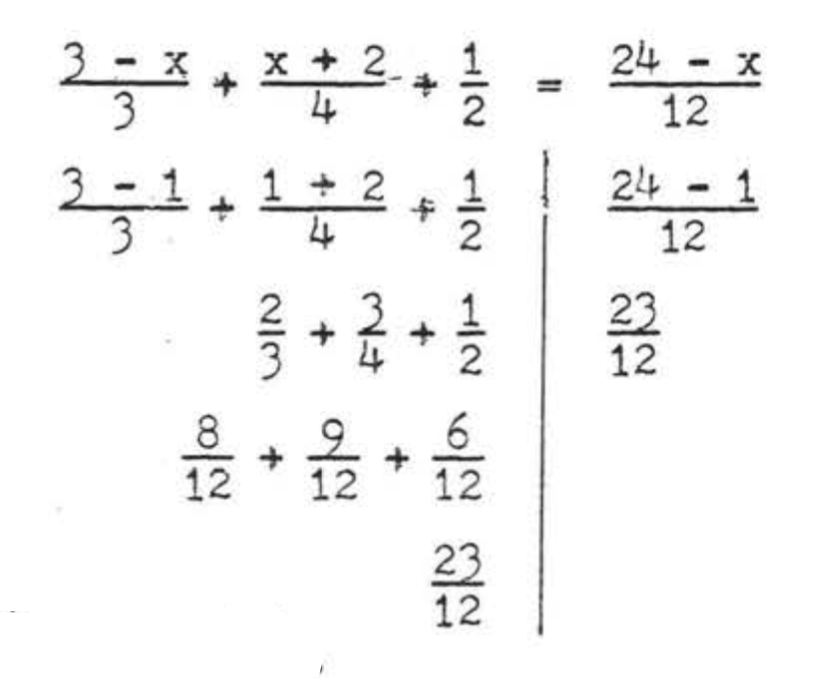
Respuesta:\(\dfrac{24 - x}{12}\),\(\dfrac{23}{12}\).
Problemas
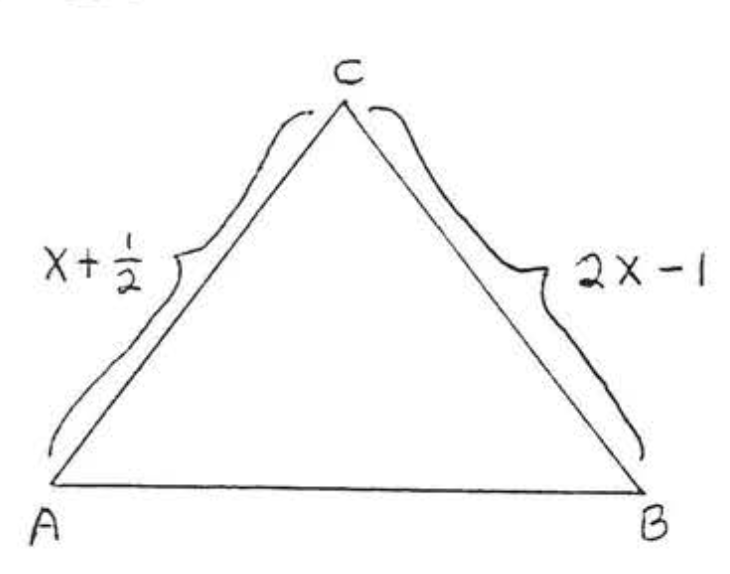
1 - 2. Encuentra\(x\) si\(\triangle ABC\) es isósceles con\(AC = BC\):
1. 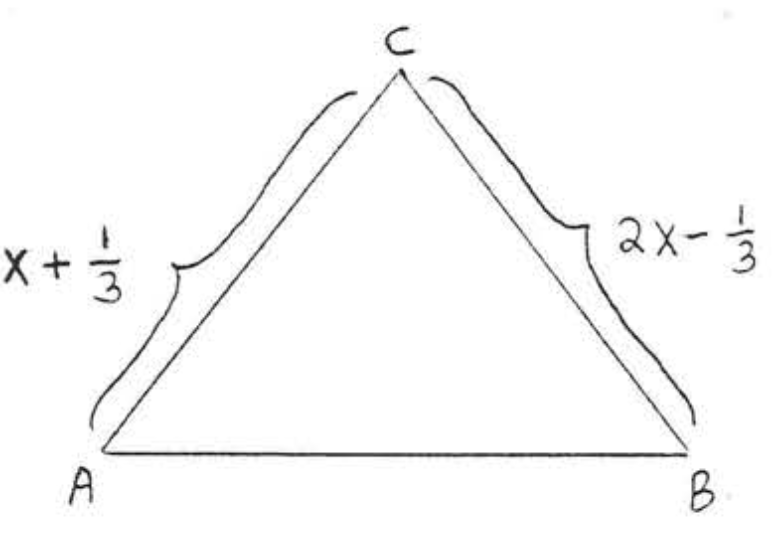 2.
2. 
3 - 4. Encuentra\(x\) si\(\triangle ABC\) es equilátero:
3. 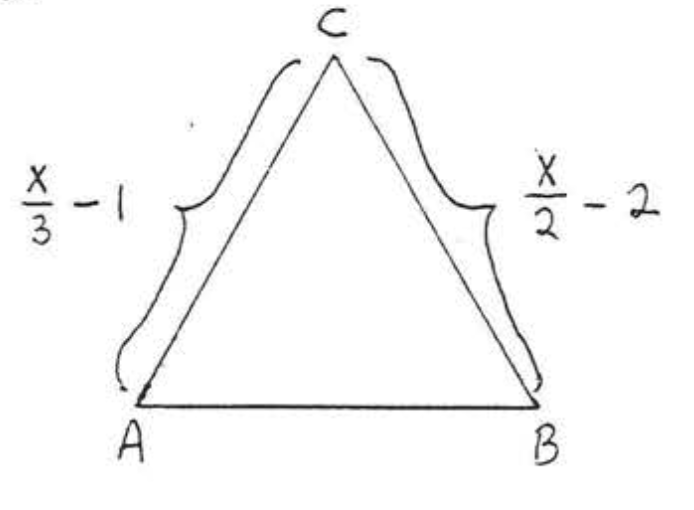 4.
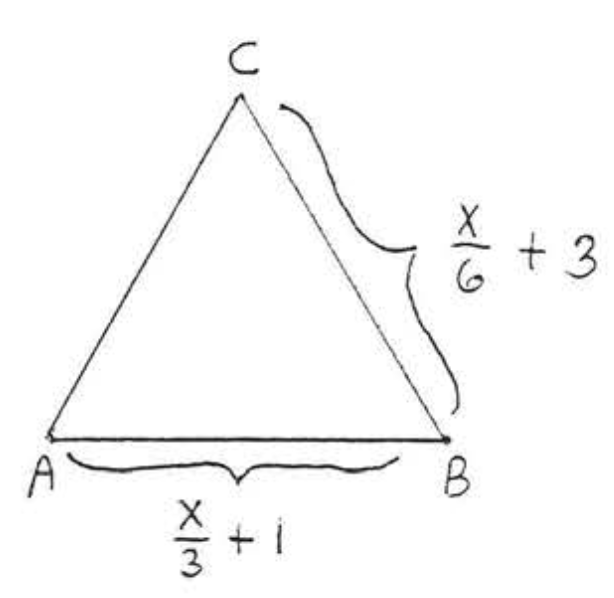
4. 
5 - 6. \(AB\)Averiguar si\(CD\) es una mediana:
5. 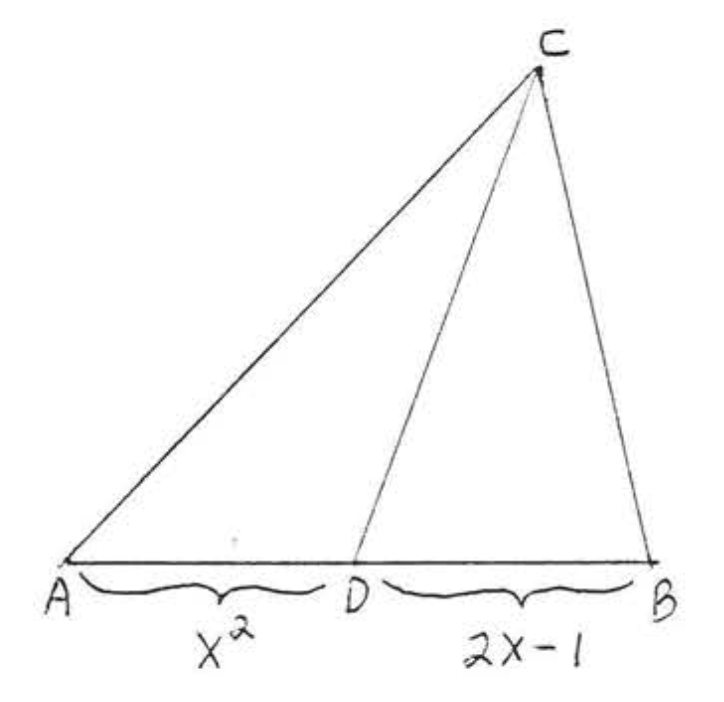 6.
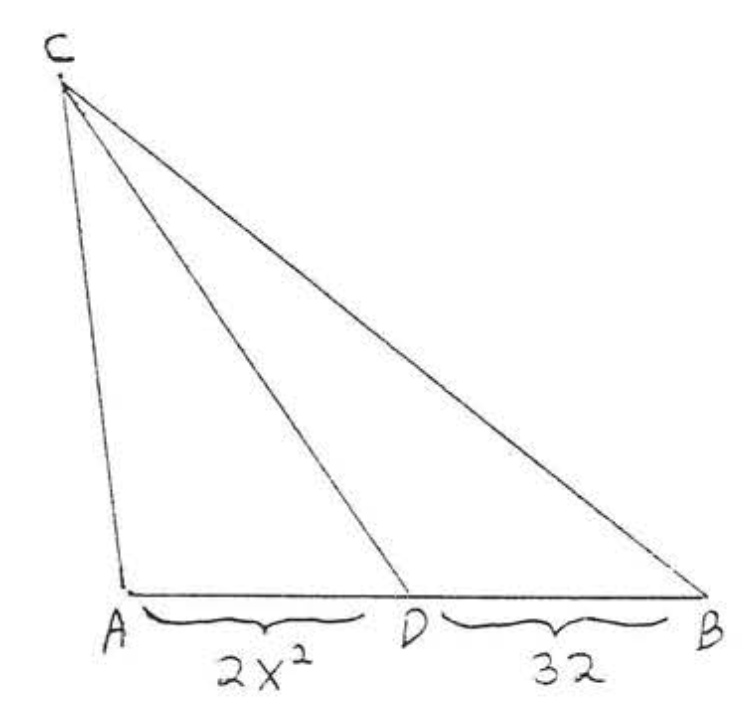
6. 
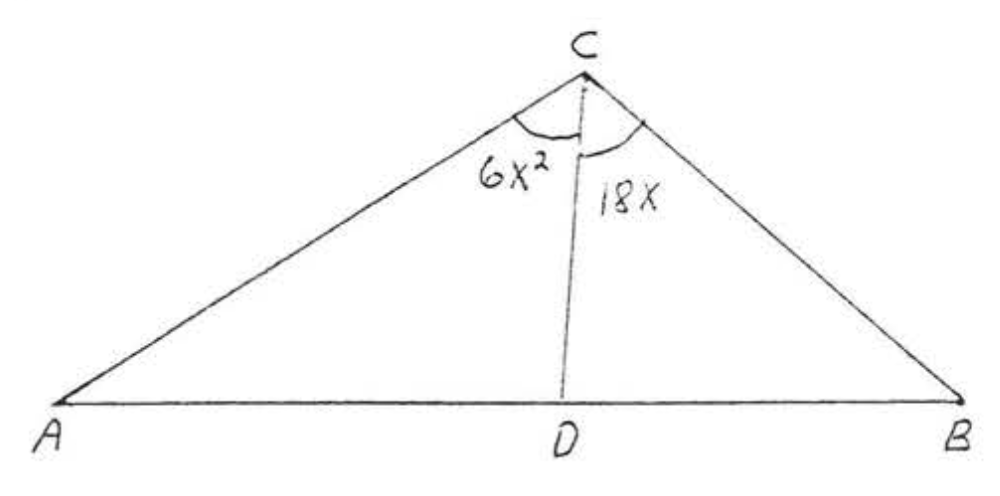
7 - 8. Encuentra\(\angle ACB\) si\(\overrightarrow{CD}\) es un ángulo bisectriz:
7. 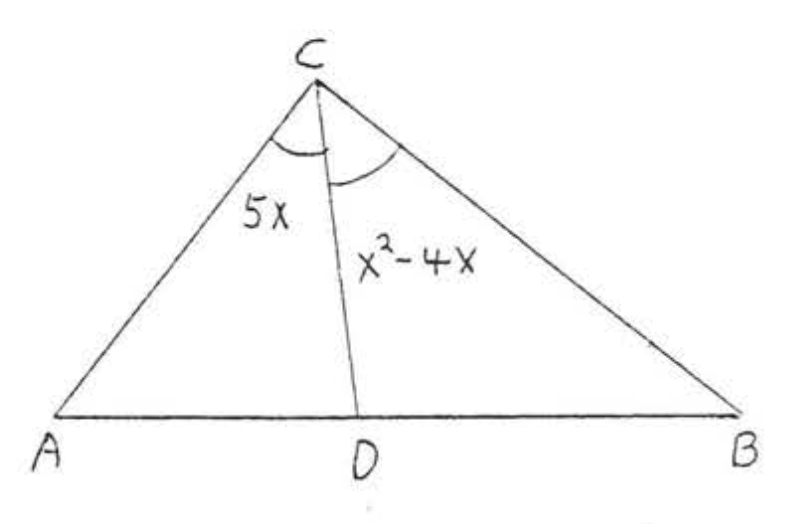 8.
8. 
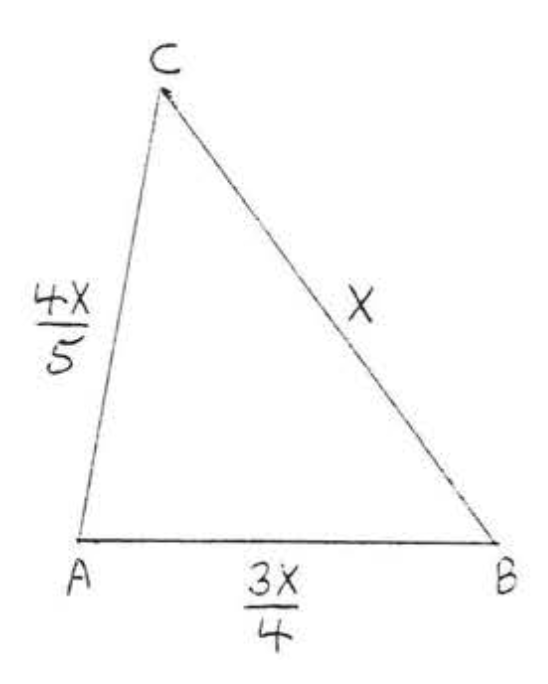
9 - 10. Encuentra el perímetro del triángulo en términos de\(x\), Luego encuentra el perímetro si\(x = 4\):
9. 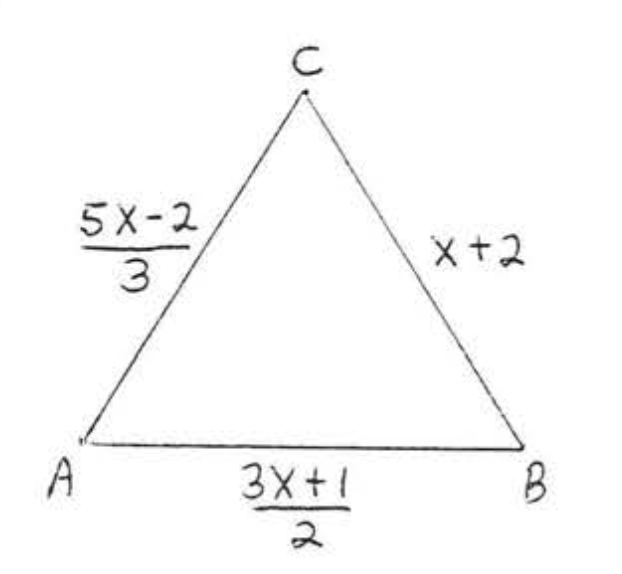 10.
10. 
11. Encuentra\(x\) si el perímetro de\(\triangle ABC\) es 33.
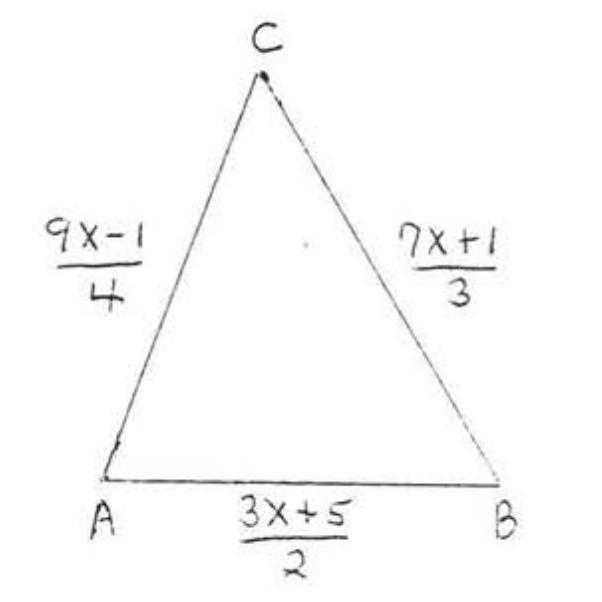
12. Encuentra\(x\) si el perímetro de\(\triangle ABC\) es 11.