1.5: Triángulos
- Page ID
- 114566
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Se forma un triángulo cuando tres segmentos de línea recta delimitan una parte del plano. Los segmentos de línea se llaman los lados del triángulo. Un punto donde dos lados se encuentran se llama vértice del triángulo, y el ángulo formado se llama ángulo del triángulo. El símbolo para triángulo es\(\triangle\).
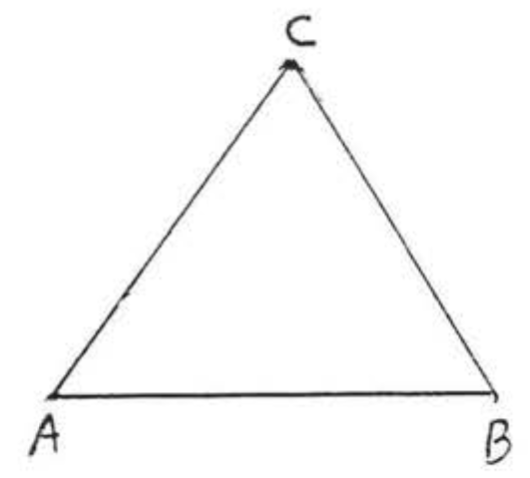
El triángulo en la Figura\(\PageIndex{1}\) se denota por\(\triangle ABC\) (\(\triangle BCA\)o o\(\triangle CAB\), etc.).
- Sus lados son\(AB\),\(AC\), y\(BC\).
- Sus vértices son\(A, B\), y\(C\).
- Sus ángulos son\(\angle A\),\(\angle B\), y\(\angle C\).
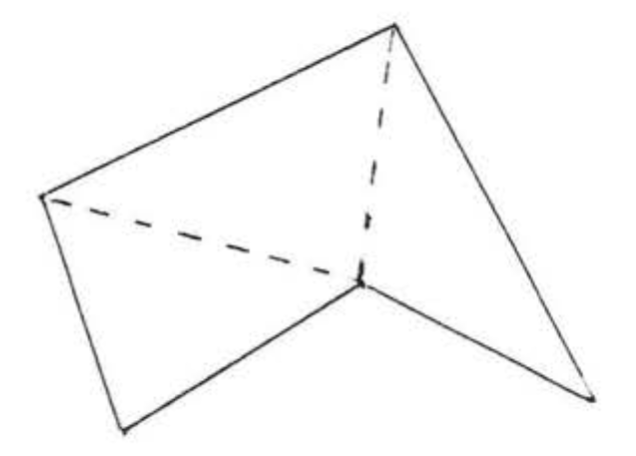
El triángulo es la figura más importante en geometría plana, esto se debe a que las figuras con más de tres lados siempre se pueden dividir en triángulos (Figura\(\PageIndex{2}\)). Si conocemos las propiedades de un triángulo, podemos extender este conocimiento al estudio de otras figuras también.
Una propiedad fundamental de los triángulos es la siguiente:
La suma de los ángulos de un triángulo es\(180^{\circ}\).
En\(\triangle ABC\) de la Figura\(\PageIndex{1}\), \(\angle A + \angle B + \angle C = 180^{\circ}\).
Encuentra\(\angle C\):
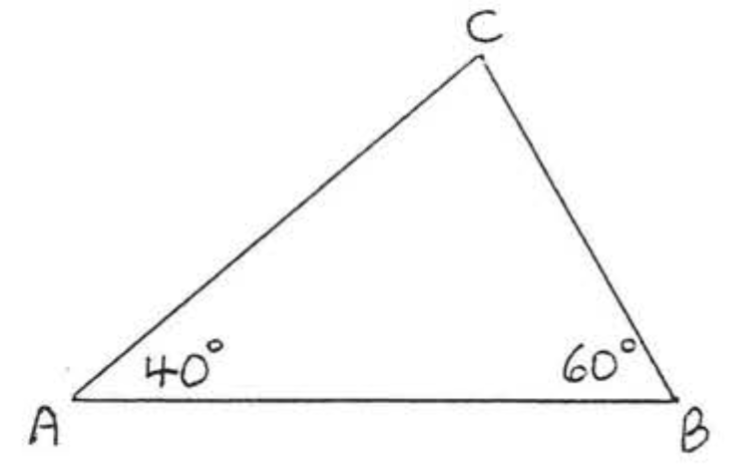
Solución
\[\begin{array} {rcl} {\angle A + \angle B + \angle C} & = & {180^{\circ}} \\ {40^{\circ} + 60^{\circ} + \angle C} & = & {180^{\circ}} \\ {100^{\circ} + \angle C} & = & {180^{\circ}} \\ {\angle C} & = & {180^{\circ} - 100^{\circ}} \\ {\angle C} & = & {80^{\circ}} \end{array} \nonumber\]
Respuesta:\(\angle C = 80^{\circ}\)
Prueba de Teorema\(\PageIndex{1}\): A través del\(C\) sorteo\(DE\) paralelo a\(AB\) (ver Figura\(\PageIndex{3}\)). Tenga en cuenta que estamos utilizando el postulado paralelo aquí,\(\angle 1 = \angle A\) y\(\angle 3 = \angle B\) porque son ángulos interiores alternos de líneas paralelas, Por lo tanto\(\angle A + \angle B + \angle C = \angle 1 + \angle 3 + \angle 2 = 180^{\circ}\).

Podemos verificar Teorema\(\PageIndex{1}\) midiendo los ángulos de un triángulo con un prolongador y tomando la suma, Sin embargo ningún instrumento de medición es perfectamente exacto, Es razonable esperar una respuesta como\(179^{\circ}\),,\(182^{\circ}\)\(180.5^{\circ}\), etc. El propósito de nuestra prueba matemática es el de nos aseguran que la suma de los ángulos de cada triángulo debe ser exactamente\(180^{\circ}\).
Encuentra\(x\):

Solución
\[\begin{array} {rcl} {\angle A + \angle B + \angle C} & = & {180^{\circ}} \\ {2x + 3x + 4x} & = & {180} \\ {9x} & = & {180} \\ {x} & = & {20} \end{array} \nonumber\]
Comprobar:

Respuesta:\(x = 20\).
Encuentra\(y\) y\(x\):
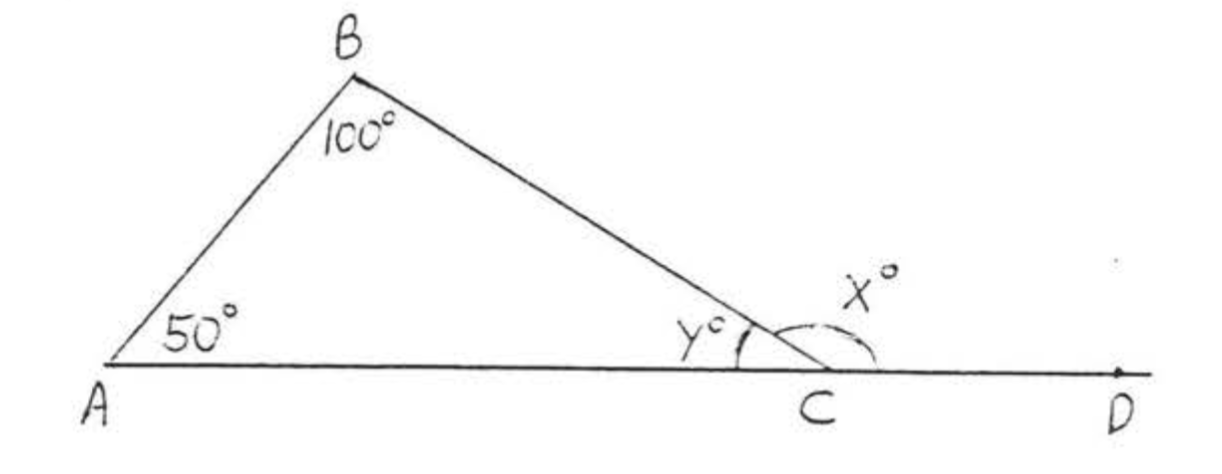
Solución
\[\begin{array} {rcl} {50 + 100 + y} & = & {180} \\ {150 + y} & = & {180} \\ {y} & = & {180 - 150} \\ {y} & = & {30} \\ {} & & {} \\ {x} & = & {180 - 30 = 150} \end{array}\]
Respuesta:\(y = 30\),\(x = 150\).
En la Figura\(\PageIndex{4}\),\(\angle x\) se denomina ángulo exterior de\(\triangle ABC\),\(\angle A\),\(\angle B\), y\(\angle y\) se denominan los ángulos interiores de\(\triangle ABC\). \(\angle A\)y\(\angle B\) se dice que son los ángulos interiores alejados del ángulo exterior\(\angle x\).
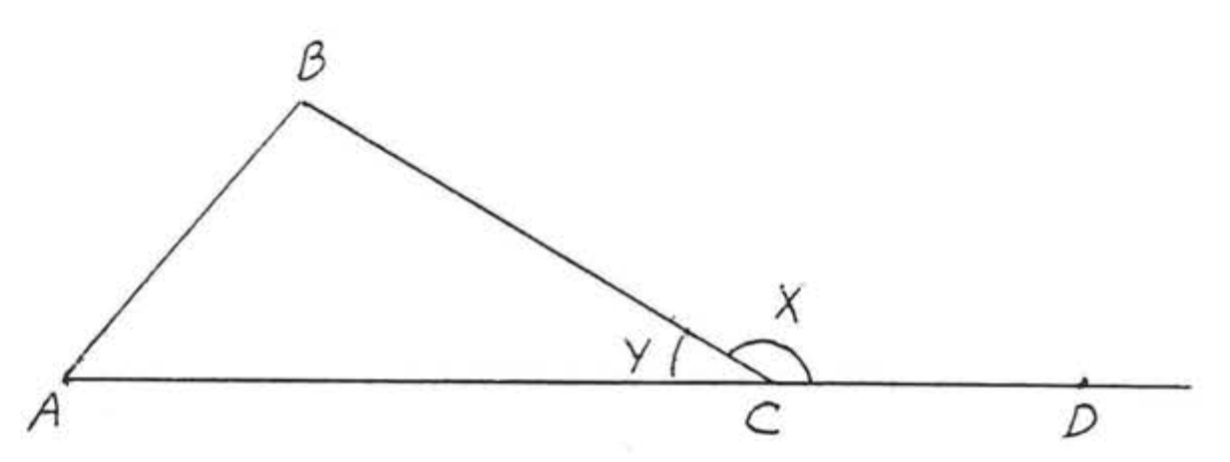
Los resultados de Ejemplo\(\PageIndex{3}\) sugieren el siguiente teorema.
Un ángulo exterior es igual a la suma de los dos ángulos interiores remotos,
En Figura\(\PageIndex{4}\),\(\angle x = \angle A + \angle B\).
Encuentra\(x\):

Solución
Usando el teorema\(\PageIndex{2}\),\(x^{\circ} = 100^{\circ} + 50^{\circ} = 150^{\circ}\).
Respuesta:\(x = 150\).
Prueba de teorema\(\PageIndex{2}\): Presentamos esta prueba en forma de doble columna, con declaraciones en la columna izquierda y el motivo de cada declaración en la columna derecha. El último enunciado es el teorema que deseamos probar.
| Declaraciones | Razones |
| 1. \(\angle A + \angle B + \angle y = 180^{\circ}\) | 1. La suma de los ángulos de un triángulo es\(180^{\circ}\). |
| 2. \(\angle A + \angle B = 180^{\circ} - \angle y\) | 2. Restar\(\angle y\) de ambos lados de la ecuación, declaración 1. |
| 3. \(\angle x = 180^{\circ} - \angle y.\) | 3. \(\angle x\)y\(\angle y\) son complementarios. |
| 4. \(\angle x = \angle A + \angle B\). | 4. Tanto\(\angle x\) (declaración 3) como\(\angle A + \angle B\) (declaración 2) son iguales\(180^{\circ} - \angle y\). |
Encuentra\(x\):
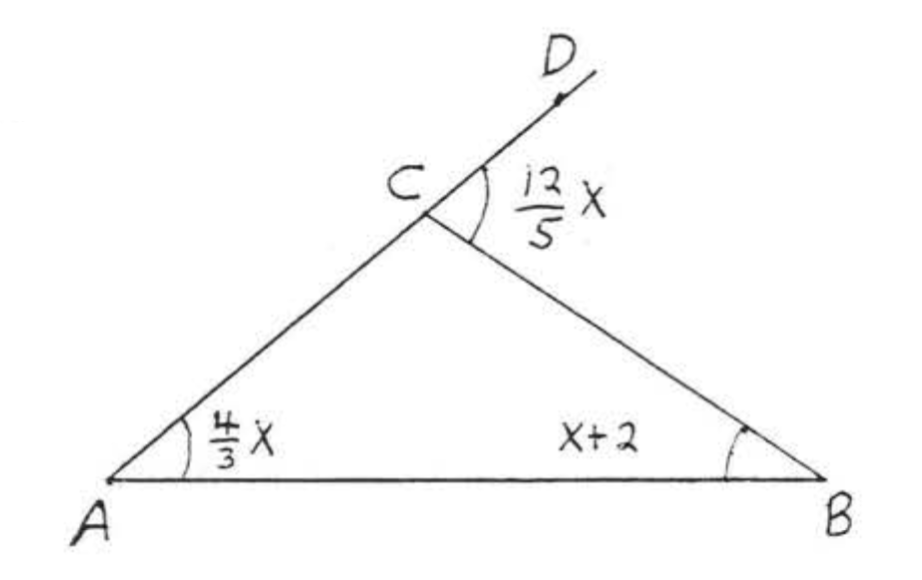
Solución
\(\angle BCD\)es un ángulo exterior con ángulos interiores remotos\(\angle A\) y\(\angle B\). Por teorema\(\PageIndex{2}\),
\[\begin{array} {rcl} {\angle BCD} & = & {\angle A + \angle B} \\ {\dfrac{12}{5} x} & = & {\dfrac{4}{3} x + x + 2} \end{array}\]
El mínimo común denominador (1, c, d) es 15.
\[\begin{array} {rcl} {\begin{array} {c} {^3} \\ {(\cancel{15})} \end{array} \dfrac{12}{\cancel{5}} x} & = & {\begin{array} {c} {^3} \\ {(\cancel{15})} \end{array} \dfrac{4}{\cancel{3}} x + (15)x + (15)(2)} \\ {36x} & = & {20x + 15x + 30} \\ {36x} & = & {35x + 30} \\ {36x - 35x} & = & {30} \\ {x} & = & {30} \end{array} \nonumber\]
Comprobar:
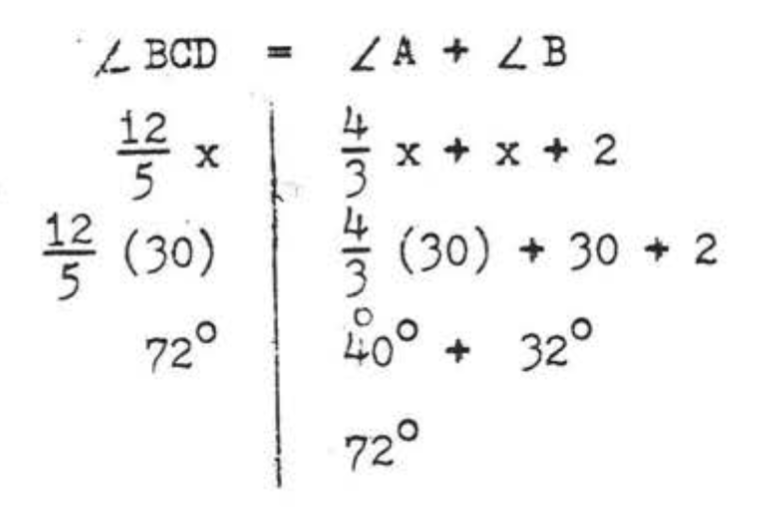
Respuesta:\(x = 30\).
Nuestro trabajo sobre la suma de los ángulos de un triángulo se puede extender fácilmente a otras figuras:
Encuentra la suma de los ángulos de un cuadrilátero (figura de cuatro lados),
Solución
Divida el cuadrilátero en dos triángulos como se ilustra,
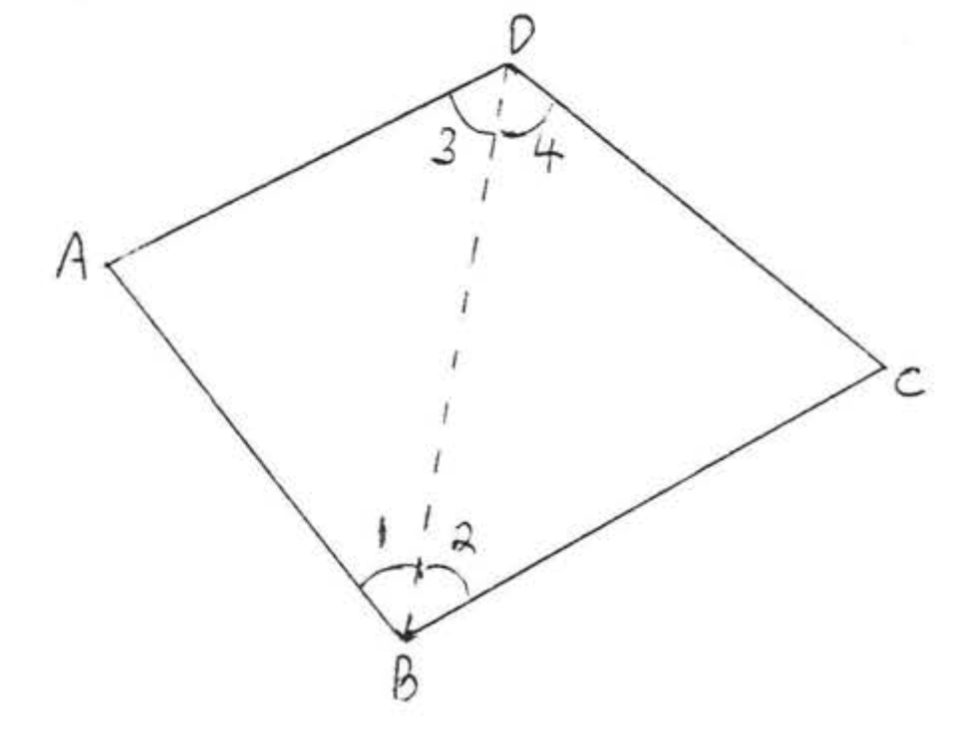
\[\begin{array} {rcl} {\angle A + \angle B + \angle C + \angle D} & = & {\angle A + \angle 1 + \angle 3 + \angle 2 + \angle 4 + \angle C} \\ {} & = & {180^{\circ} + 180^{\circ}} \\ {} & = & {360^{\circ}} \end{array} \nonumber\]
Respuesta:\(360^{\circ}\).
Encuentra la suma de los ángulos de un pentágono (figura de cinco lados).
Solución
Divide el pentágono en tres triángulos como se ilustra, La suma es igual a la suma de los ángulos de los tres triángulos =\((3)(180^{\circ}) = 540^{\circ}\).
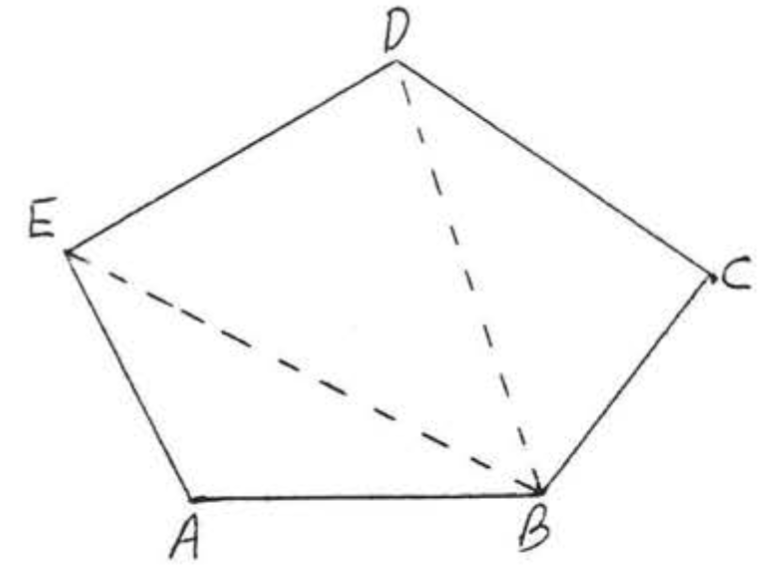
Respuesta:\(540^{\circ}\).
Hay un principio más simple que derivaremos del Teorema\(\PageIndex{1}\), Consideremos los dos triángulos en la Figura\(\PageIndex{5}\).

Se nos da eso\(\angle A = \angle D = 60^{\circ}\) y\(\angle B = \angle E = 40^{\circ}\). Un breve cálculo muestra que también debemos tener\(\angle C = \angle F = 80^{\circ}\). Esto sugiere el siguiente teorema:
Si dos ángulos de un triángulo son iguales respectivamente a dos ángulos de otro triángulo, entonces sus ángulos restantes también son iguales.
En la Figura\(\PageIndex{6}\), if \(\angle A = \angle D\) and \(\angle B = \angle E\) then \(\angle C = \angle F\).
- Prueba
-
\(\angle C = 180^{\circ} - (\angle A + \angle B) = 180^{\circ} - (\angle D + \angle E) = \angle F\).

Figura\(\PageIndex{6}\). \(\angle A = \angle D\) and \(\angle B = \angle E\).
Nuestro Teorema\(\PageIndex{1}\), que establece que la suma de los ángulos de un triángulo es\(180^{\circ}\), es una de las consecuencias más importantes del postulado paralelo, Por lo tanto, una forma de probar la verdad del postulado paralelo (ver la Nota Histórica en la Sección 1.4) es probar el verdad del teorema\(\PageIndex{1}\), Esto en realidad fue probado por el matemático, astrónomo y físico alemán, Karl Friedrich Gauss (1777 - 1855). (Este es el mismo Gauss cuyo nombre se utiliza como unidad de medida en la teoría del magnetismo), Gauss midió la suma de los ángulos del triángulo formado por tres picos montañosos en Alemania, encontró que la suma de los ángulos era 14.85 segundos más que\(180^{\circ}\) (60 segundos 1 minuto, 60 minutos = 1 grado). Sin embargo, este pequeño exceso podría haberse debido a un error experimental, por lo que la suma podría haber sido en realidad\(180^{\circ}\).
Aparte del error experimental, hay otra dificultad involucrada en verificar el teorema de la suma de ángulos. Según la geometría no euclidiana de Lobachevsky, la suma de los ángulos de un triángulo es siempre menor que\(180^{\circ}\). En la geometría no euclidiana de Riemann, la suma de los ángulos es siempre mayor que\(180^{\circ}\), sin embargo en ambos casos la diferencia de\(180^{\circ}\) es insignificante a menos que el triángulo sea muy grande, Ni teoría nos dice exactamente cuán grande debería ser tal triángulo, Incluso si medimos los ángulos de un muy triángulo grande, como uno formado por tres estrellas, y encontró que la suma era indistinguible de\(180^{\circ}\), solo podríamos decir que el teorema de la suma angular y el postulado paralelo son aparentemente ciertos para estas grandes distancias, Estas distancias aún podrían ser demasiado pequeñas para permitirnos determinar quésistema geométrico describe mejor el universo como un todo,
Problemas
1 - 12. Encuentra\(x\) y todos los ángulos que faltan de cada triángulo:
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 
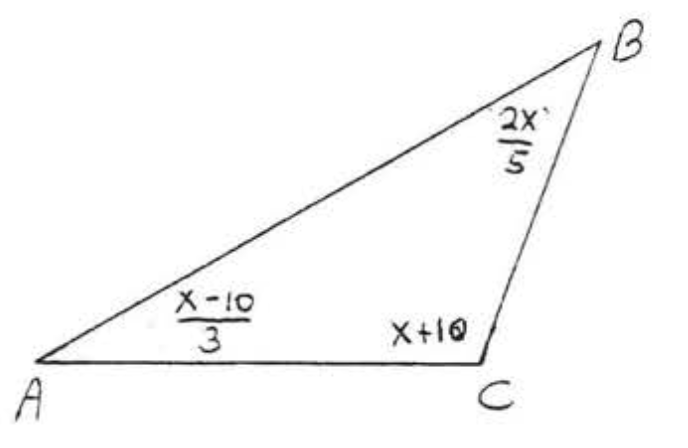
11.  12.
12. 
13 - 14. Buscar\(x, y\), y\(z\):
13. 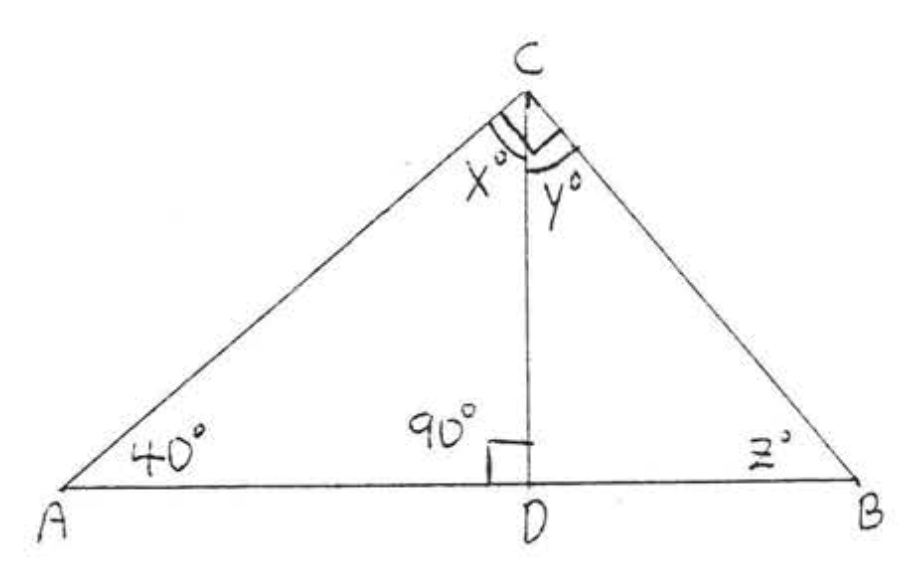 14.
14. 
15 - 20. Encuentra\(x\):
15.  16.
16. 
17.  18.
18. 
19.  20.
20. 
21. Encuentra la suma de los ángulos de un hexágono (figura de 6 lados).
22. Encuentra la suma de los ángulos de un octágono (figura de 8 lados).
23 - 26. Encuentra\(x\):
23.  24.
24. 
25.  26.
26. 


