4.6: Distancia de un punto a una línea
- Page ID
- 114611
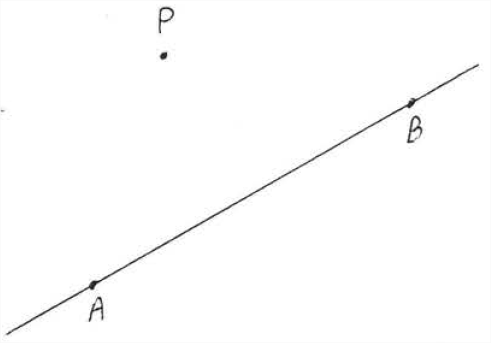
Supongamos que se nos da un punto\(P\) y una línea\(\overleftrightarrow{AB}\) como en la Figura\(\PageIndex{1}\). Nos gustaría encontrar el segmento de línea más corto que se pueda dibujar desde\(P\) hasta\(\overleftrightarrow{AB}\).
Primero probaremos un teorema:
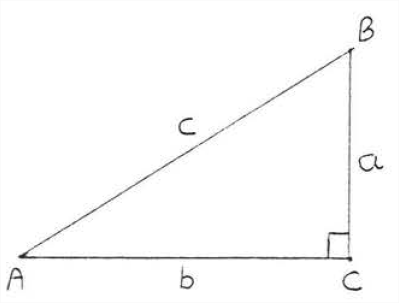
En un triángulo rectángulo, la hipotenusa es más grande que cualquiera de las piernas. En Figura\(\PageIndex{1}\),\(c>a\) y\(c>b\). (El símbolo “>” significa “es mayor que”.)
- Prueba
-
Por el Teorema de Pitágoras,
\(c = \sqrt{a^2 + b^2} > \sqrt{a^2} = a.\)
\(c = \sqrt{a^2 + b^2} > \sqrt{b^2} = b.\)
Ahora podemos dar la respuesta a nuestra pregunta:
La perpendicular es el segmento de línea más corto que se puede dibujar de un punto a una línea recta.
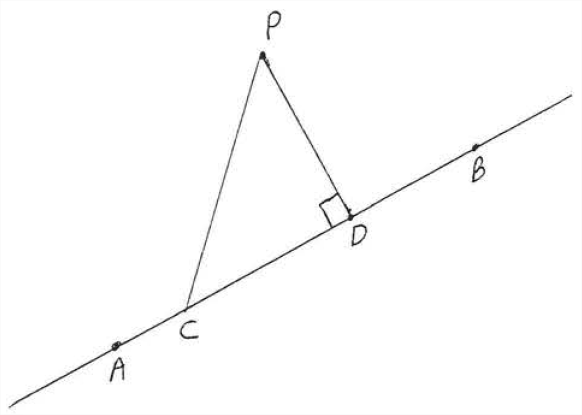
En\(\PageIndex{3}\) la Figura el segmento de línea más corto de\(P\) a\(\overleftrightarrow{AB}\) es\(PD\). Cualquier otro segmento de línea, como\(PC\), debe ser más largo.
- Prueba
-
\(PC\)es la hipotenusa del triángulo rectángulo\(PCD\). Por lo tanto por Teorema\(\PageIndex{1}\),\(PC > PD\).
Definimos la distancia de un punto a una línea para que sea la longitud de la perpendicular.
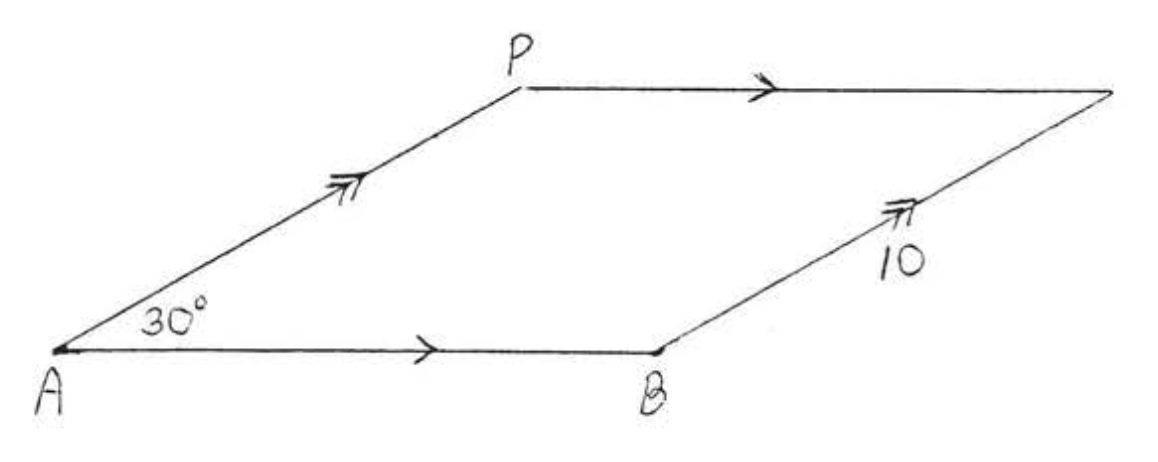
Encuentra la distancia desde\(P\) hasta\(\overleftrightarrow{AB}\):
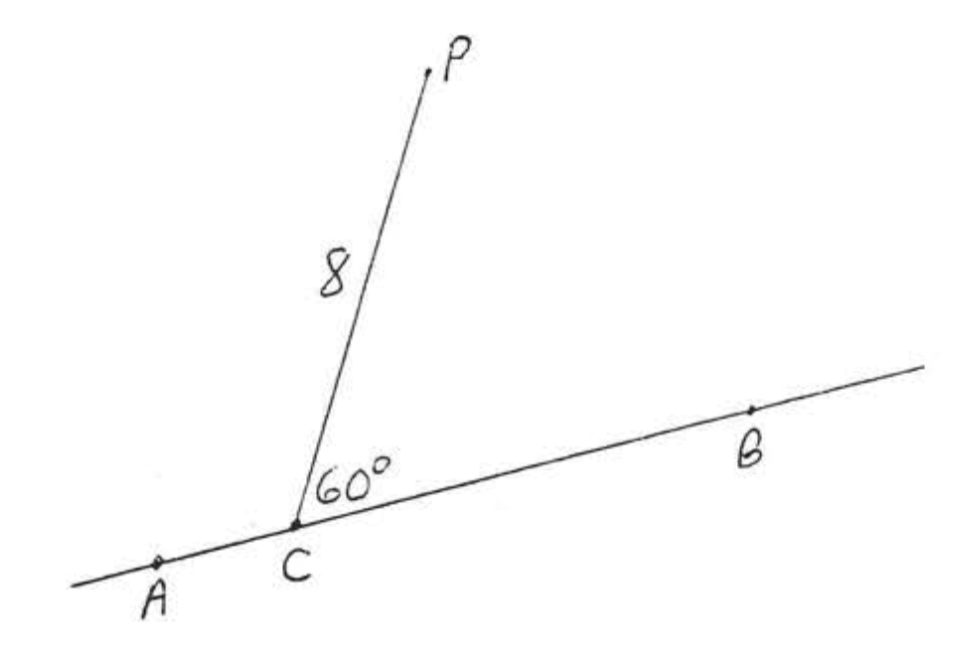
Solución
Dibujar\(PD\) perpendicular a\(\overleftrightarrow{AB}\) (Figura\(\PageIndex{4}\)). \(\triangle PCD\)es un\(30^{\circ}-60^{\circ}-90^{\circ}\) triángulo.
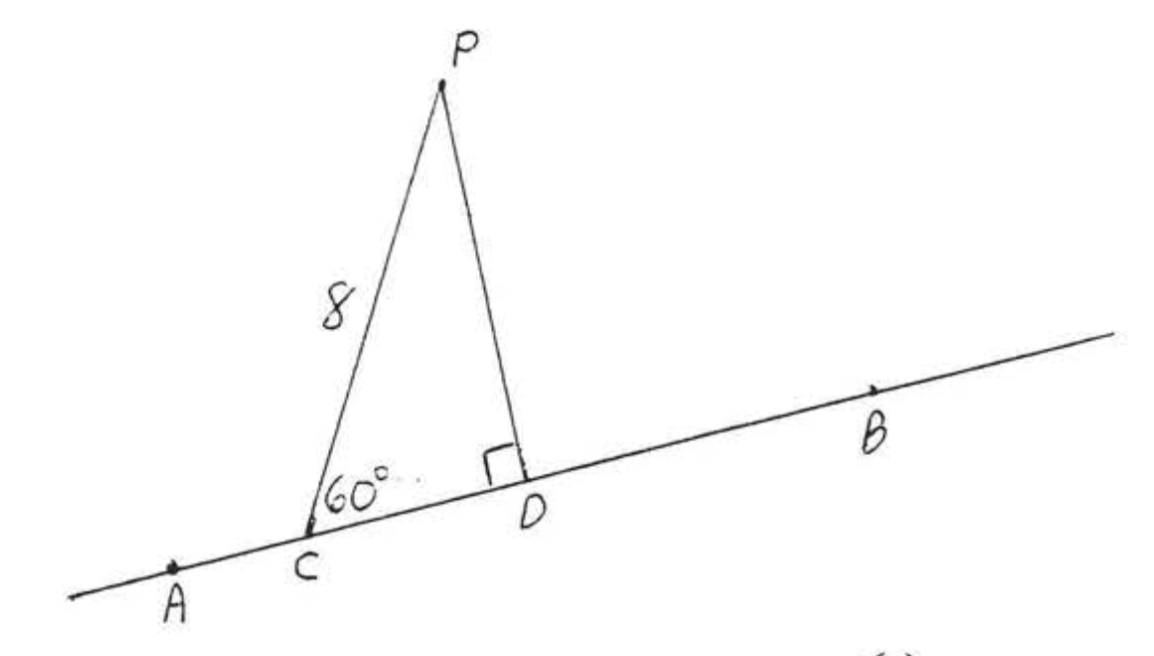
\(\begin{array} {rcl} {\text{hyp}} & = & {2s} \\ {8} & = & {2(CD)} \\ {4} & = & {CD} \\ {L} & = & {s\sqrt{3}} \\ {PD} & = & {4\sqrt{3}} \end{array}\)
Respuesta:\(4\sqrt{3}\)
Problemas
1 - 6. Encuentra la distancia desde\(P\) hasta\(\overleftrightarrow{AB}\):
1.
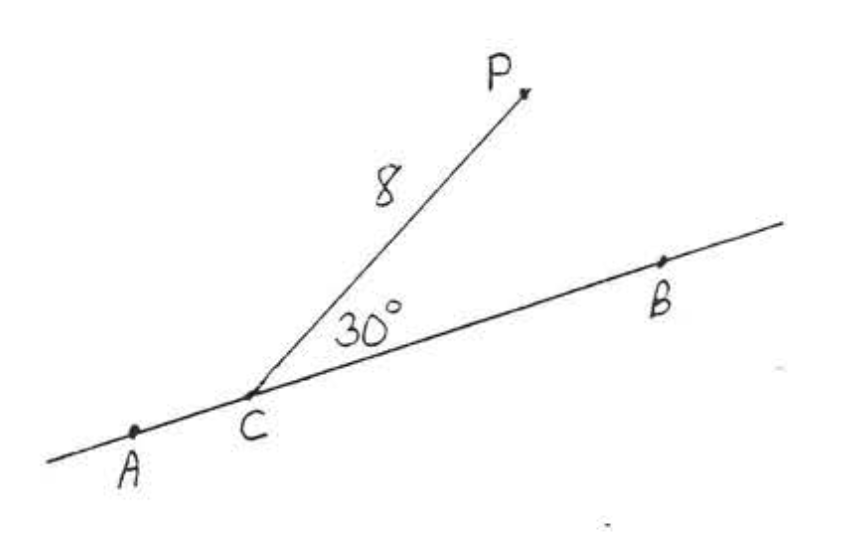
2.
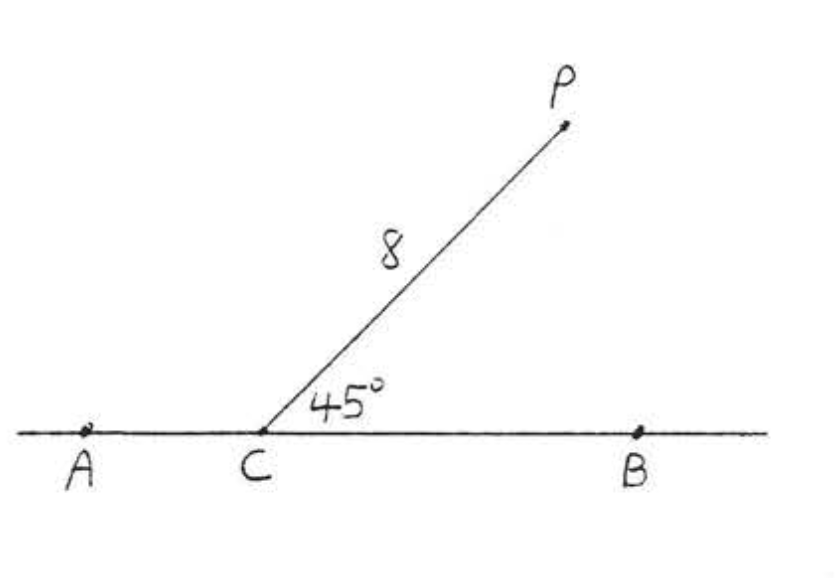
3.
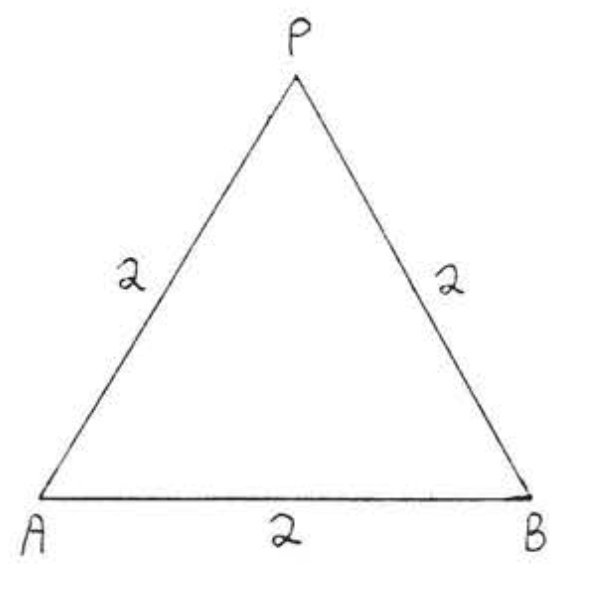
4.
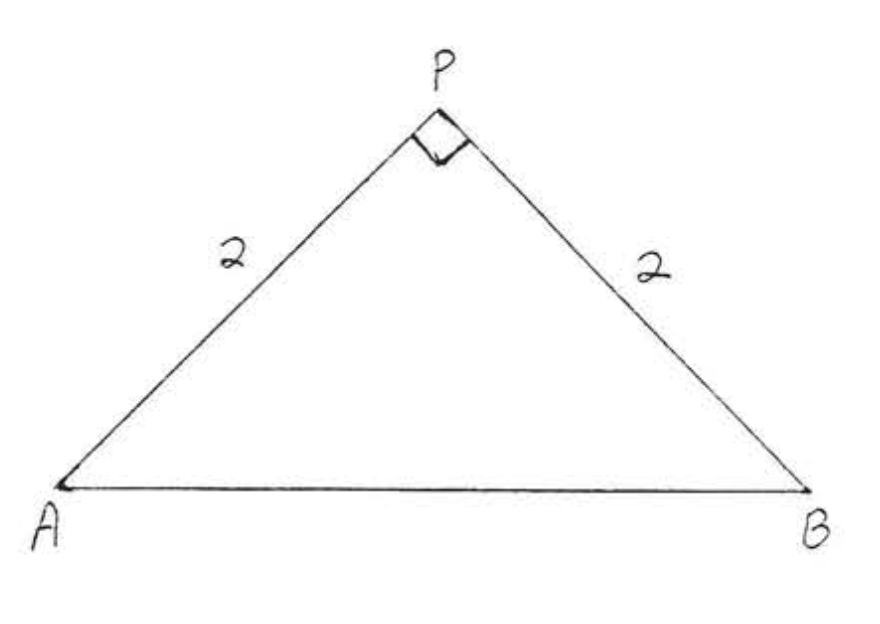
5.
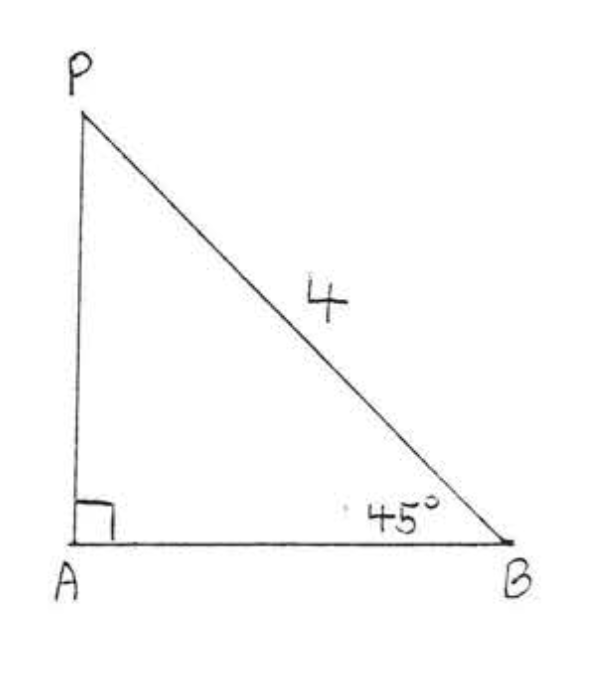
6.