6.1: El Área de un Rectángulo y Cuadrado
- Page ID
- 114662
La medición del área de figuras geométricas es una de las formas más familiares en las que se utiliza la matemática en nuestra vida cotidiana. El espacio del piso de un edificio, la estae de una imagen, la cantidad de papel en un rollo de toallas de papel son ejemplos de Artículos que a menudo se miden en términos de área. En este capítulo derivaremos fórmulas para las áreas de los objetos geométricos que hemos estudiado.
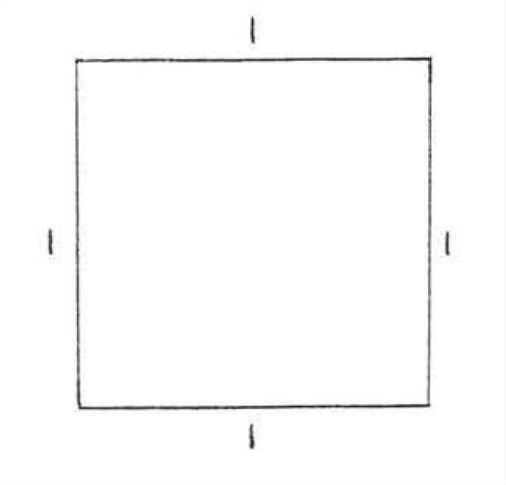
El área se mide en pulgadas cuadradas, pies cuadrados, centímetros cuadrados, etc. La unidad de medida bastc es la unidad cuadrada, el cuadrado cuyos lados son de longitud 1 (Figura\(\PageIndex{1}\)). Su área es de 1 pulgada cuadrada, 1 pie cuadrado, 1 centímetro cuadrado, etc., dependiendo de qué medida de longitud se elija. El área de cualquier figura cerrada se define como el número de cuadrados unitarios que contiene.
Encuentra el área de un rectángulo con longitud 5 y ancho 3.
Solución
Vemos por el diagrama que el área es\((5)(3)=15\)
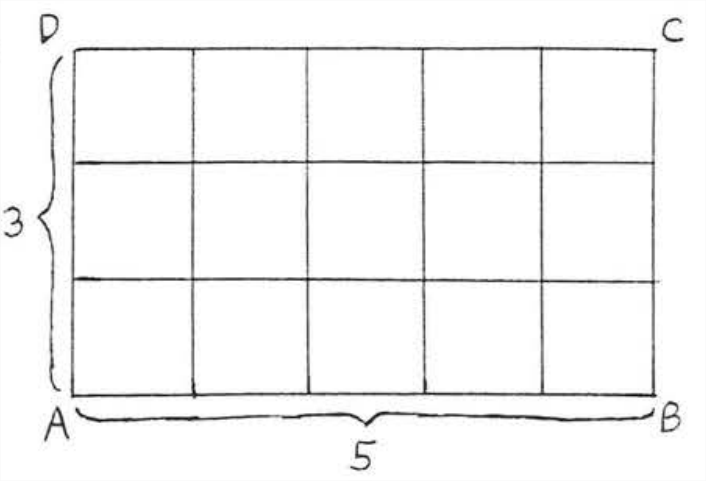
Respuesta: 15.
Esto sugiere el siguiente teorema:
El área de un rectángulo es la longitud por su ancho.
\(A = lw\)
Encuentra el área de un cuadrado con lado 3.
Solución
Área =\((3)(3) = 3^2 = 9\).
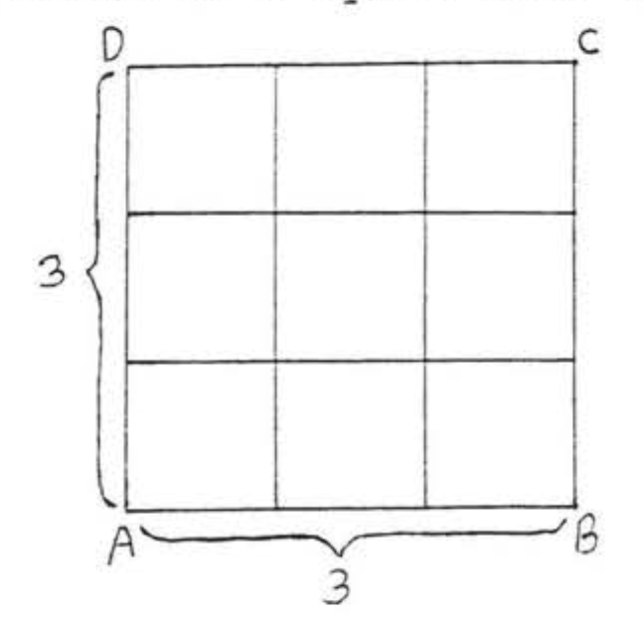
Respuesta: 9.
La fórmula para un squa:re es ahora evidente:
El área de un cuadrado es el cuadrado de uno de sus lados.
\(A = s^2\)
El perímetro de un polígono es el su.m de las longitudes de sus lados. Por ejemplo el perímetro del rectángulo de Ejemplo\(\PageIndex{1}\) sería 5 + 5 + 3 + 3 = 16.
Encuentra el área y perímetro del rectángulo\(ABCD\):
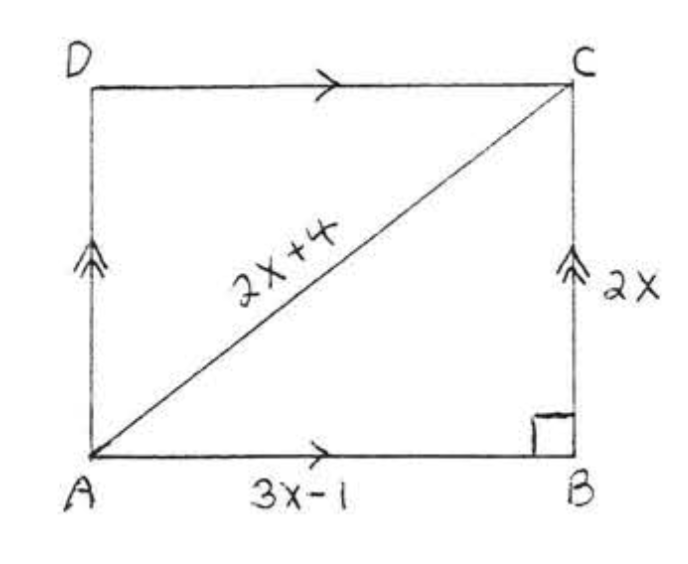
Solución
Primero usamos el Teorema de Pitágoras para encontrar\(x\):
\(\begin{array} {rcl} {AB^2 + BC^2} & = & {AC^2} \\ {(3x - 1)^2 + (2x)^2} & = & {(2x + 4)^2} \\ {9x^2 - 6 x + 1 + 4x^2} & = & {4x^2 + 16x + 16} \\ {9x^2 - 22x - 15} & = & {0} \\ {(9x + 5)(x - 3)} & = & {0} \end{array}\)
\(\begin{array} {rcl} {9x + 5} & = & {0} \\ {x} & = & {-\dfrac{5}{9}} \end{array}\)\(\begin{array} {rcl} {x - 3} & = & {0} \\ {x} & = & {3} \end{array}\)
Rechazamos la respuesta\(x = -\dfrac{5}{9}\) porque\(BC = 2x = 2(-\dfrac{5}{9}) = -\dfrac{10}{9}\) tendría longitud negativa. Por lo tanto\(x = 3\).
\(AB = 3x - 1 = 3(3) - 1 = 9 - 1 = 8\). \(BC = 2x = 2(3) = 6\).
\(AC = 2x + 4 = 2(3) + 4 = 6 + 4 = 10\).
Comprobar:

Área =\(lw = (8)(6) = 48.\) Perímetro = 8 + 8 + 6 + 6 = 28.
Respuesta: Área = 48, Perímetro = 28.
Encuentra\(x\):
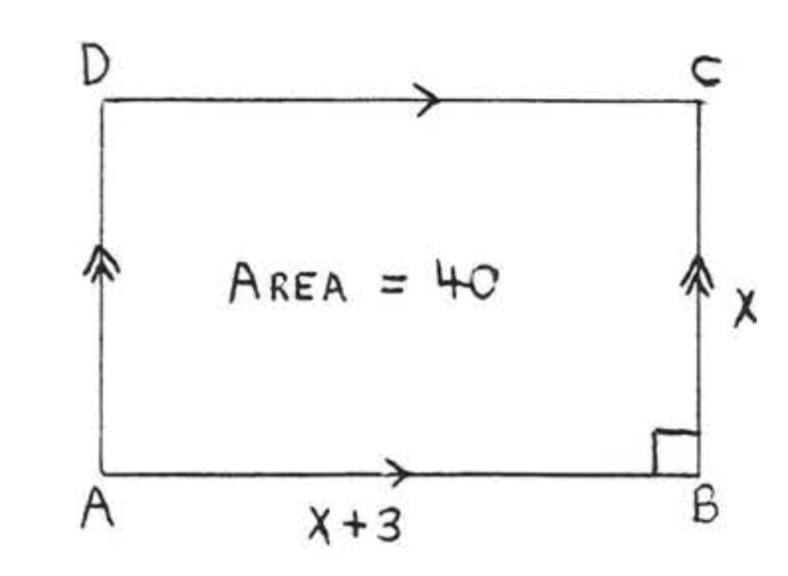
Solución
\(\begin{array} {rcl} {A} & = & {lw} \\ {40} & = & {(x + 3)(x)} \\ {40} & = & {x^2 + 3x} \\ {0} & = & {x^2 + 3x - 40} \\ {0} & = & {(x - 5)(x + 8)} \\ {x} & = & {5\ \ \ \ \ \ \ x = -8} \end{array}\)
Rechazamos\(x = -8\) porque lado\(BC = x\) del rectángulo sería negativo.
Comprobar,\(x = 5\):
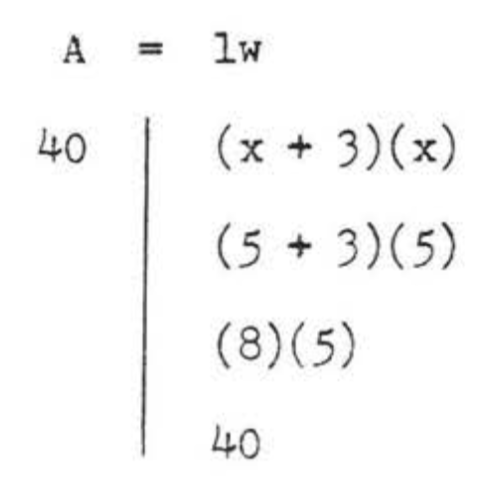
Respuesta:\(x = 5\).
Una habitación en forma de L tiene las dimensiones indicadas en el diagrama, ¿Cuántas baldosas de uno por un pie se necesitan para revestir el piso?
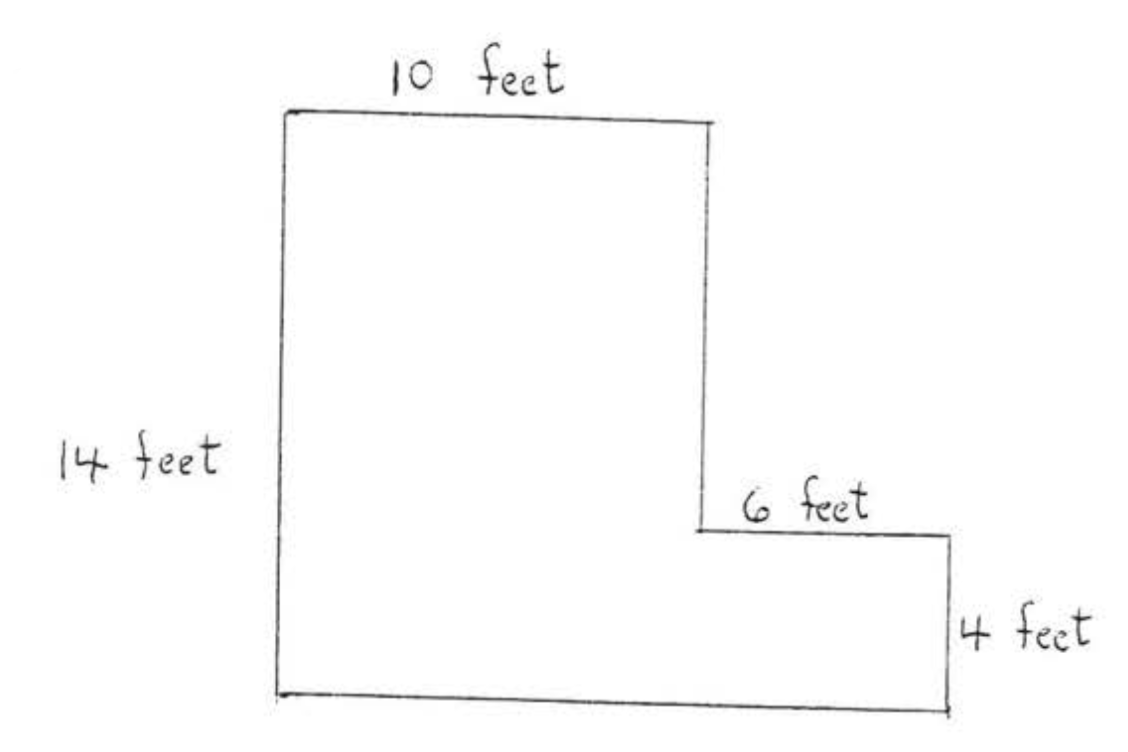
Solución
Divida la habitación en dos rectángulos como se muestra.
\(\begin{array} {rcl} {\text{Area of room}} & = & {\text{Area of large rectangle}} \\ {} & + & {\text{Area of small rectangle}} \\ {} & = & {(14)(10) + (6)(4)} \\ {} & = & {140 + 24} \\ {} & = & {\text{164 square feet.}} \end{array}\)
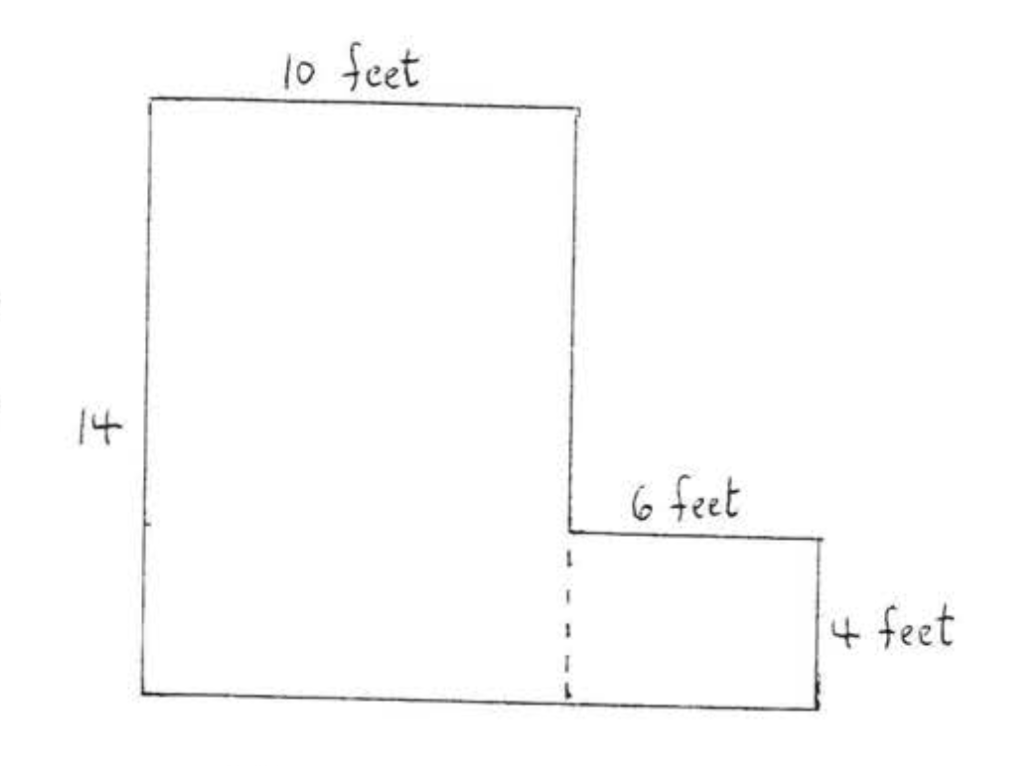
Respuesta: 164
La necesidad de medir:re áreas de tierra fue uno de los problemas antiguos que llevaron al desarrollo de la geometría. Tanto los primeros egipcios como los babilonios tenían fórmulas para las áreas de rectángulos, triángulos y trapecios, pero algunas de sus fórmulas no eran del todo precisas. Las fórmulas de este capítulo eran conocidas por los griegos y se encuentran en Elementos de Euclides.
Problemas
1 - 14. Encuentra el área y perímetro de\(ABCD\):
1.
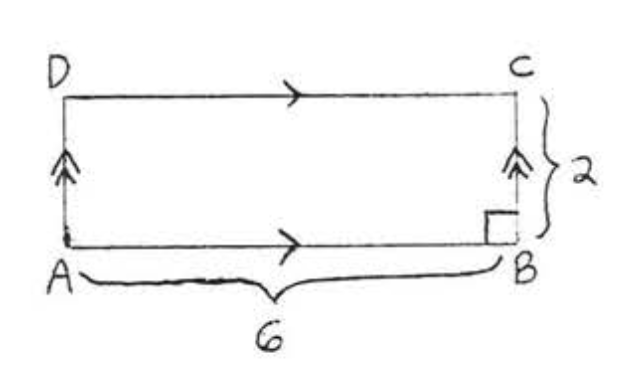
2.
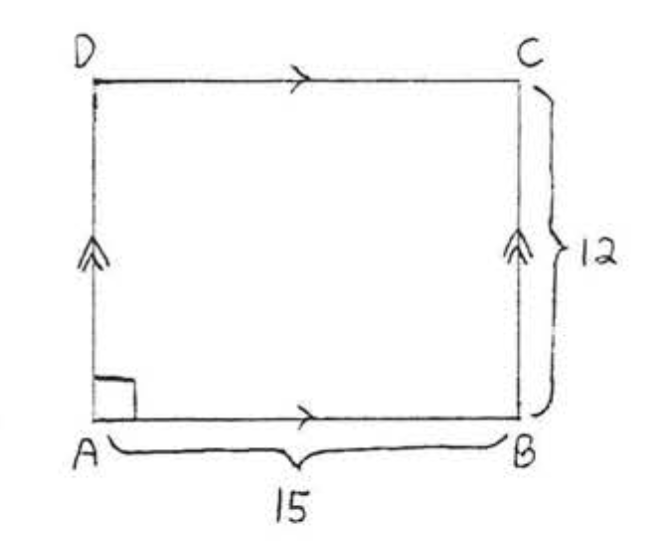
3.
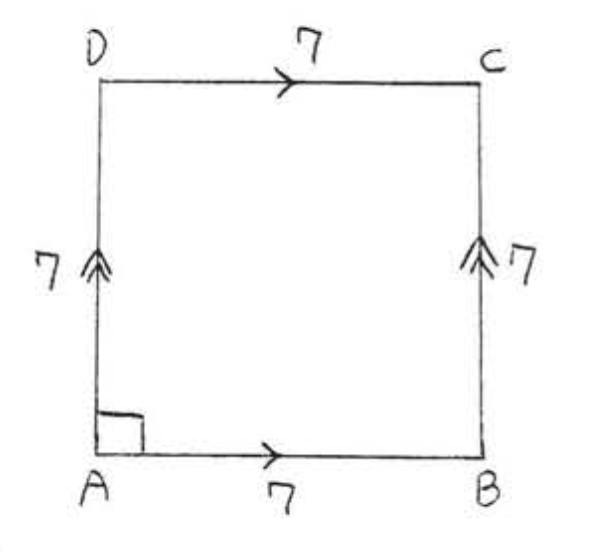
4.
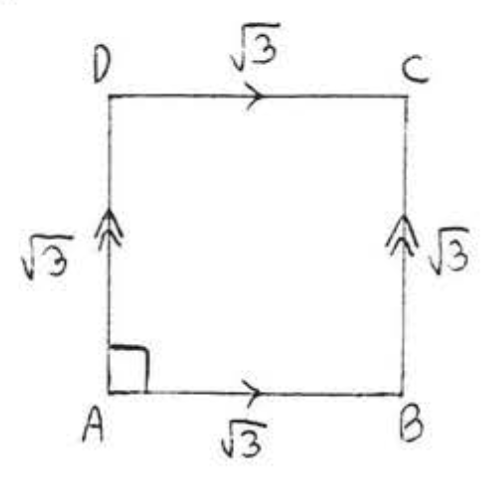
5.
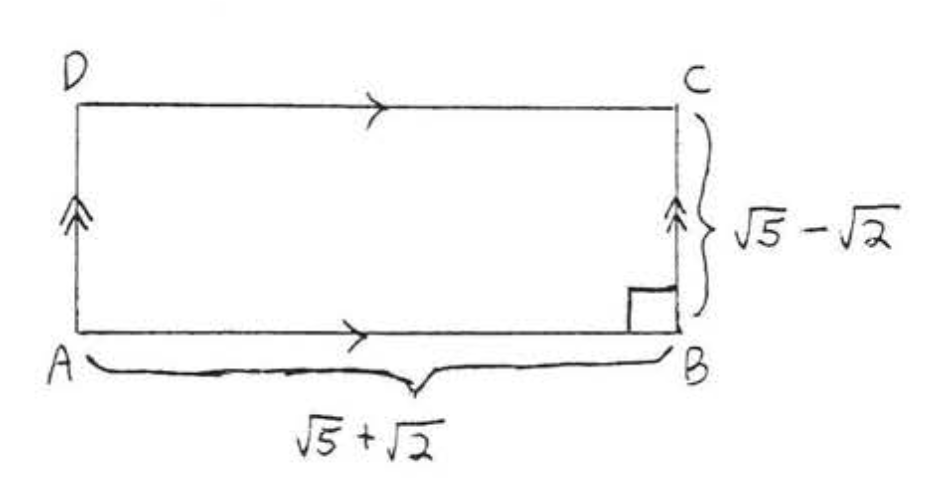
6.
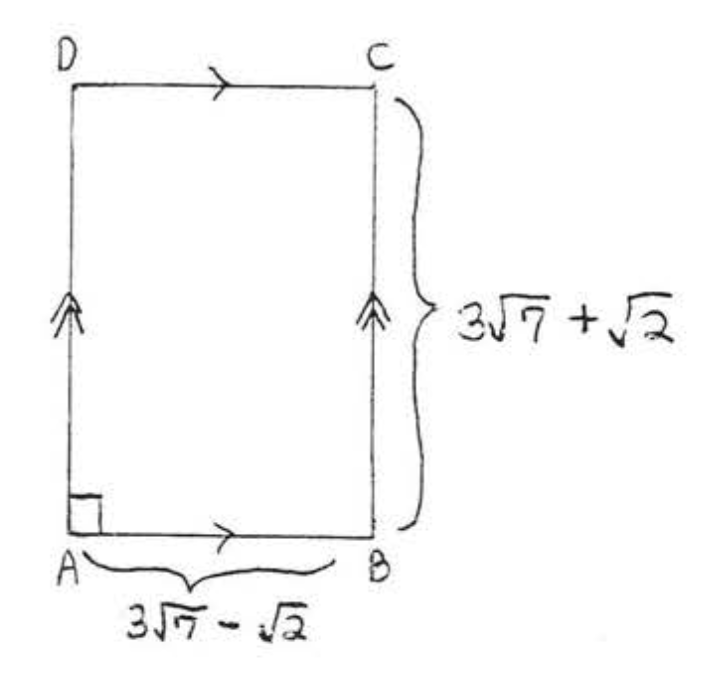
7.
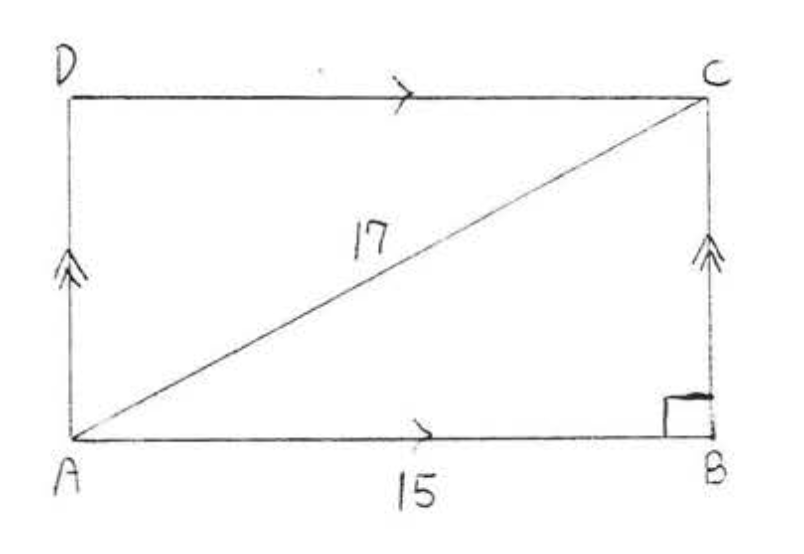
8.
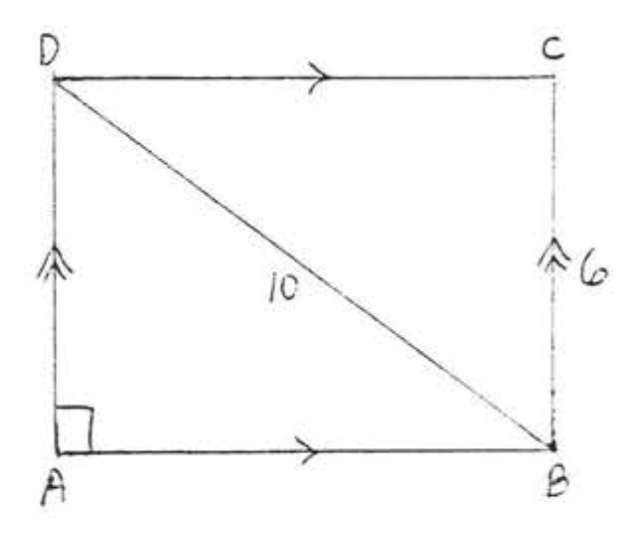
9.
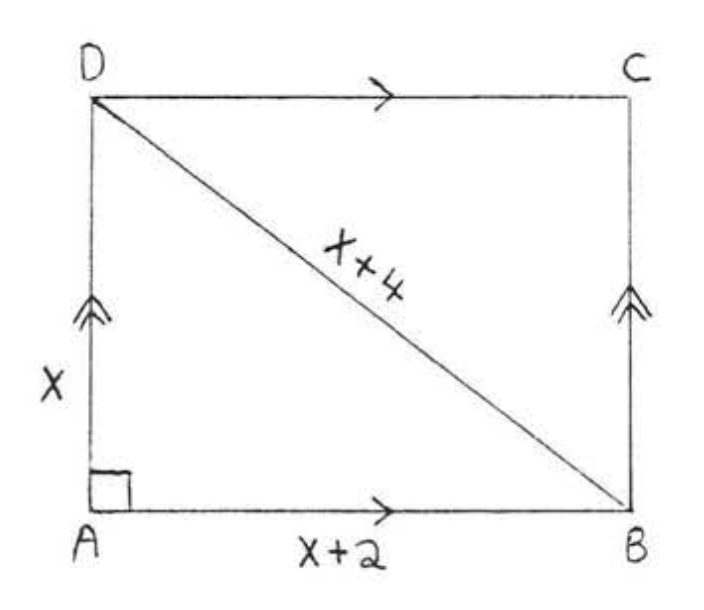
10.
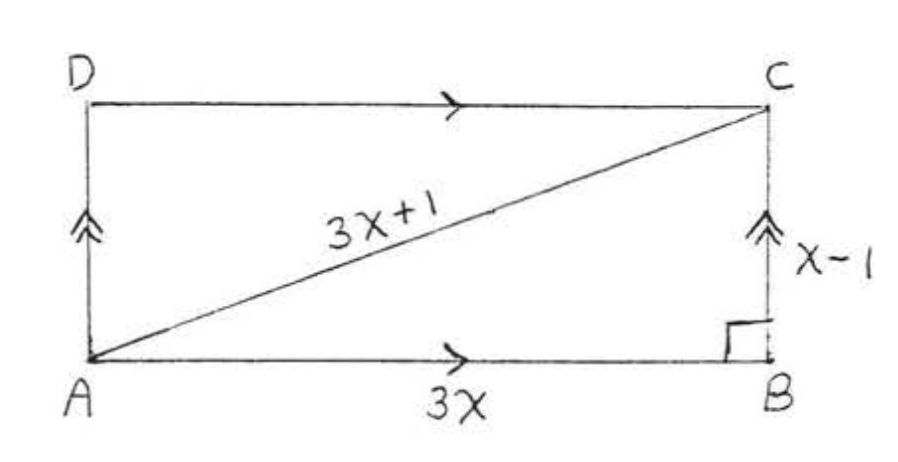
11.
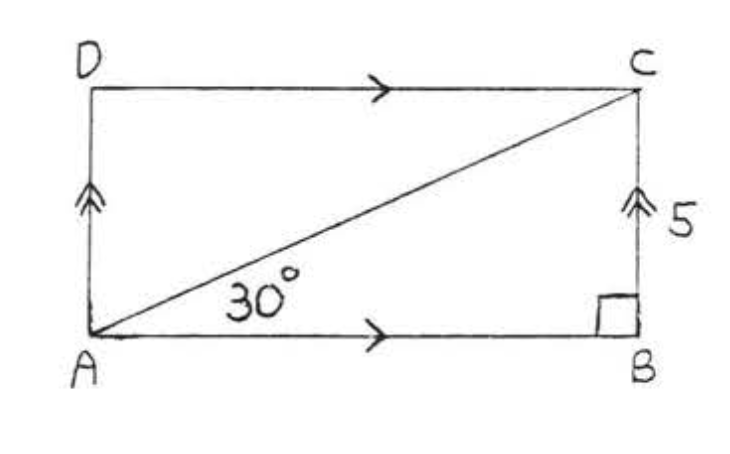
12.
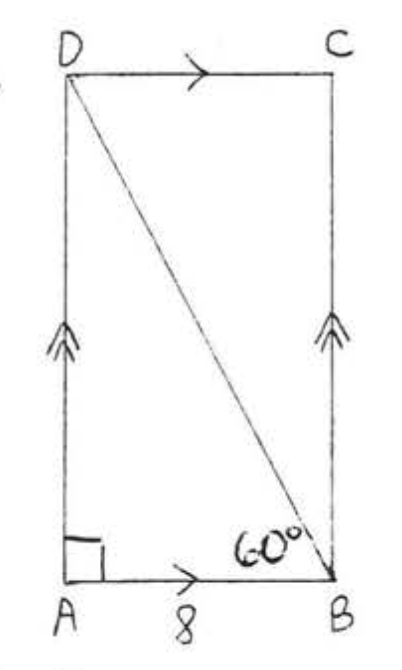
13.
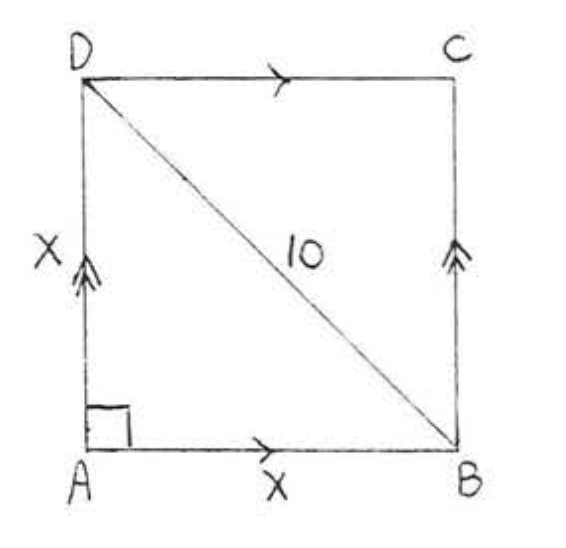
14.
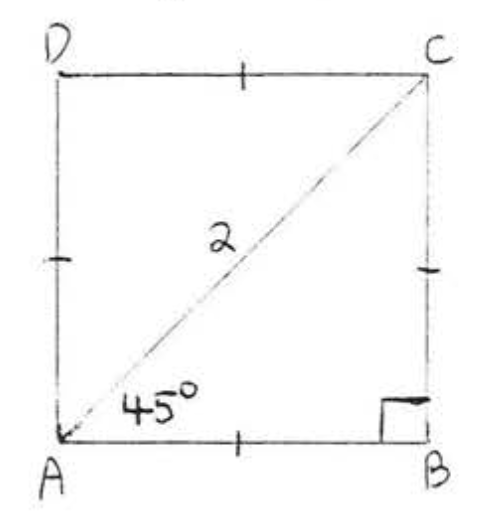
15 - 18. Encuentra\(x\):
15.
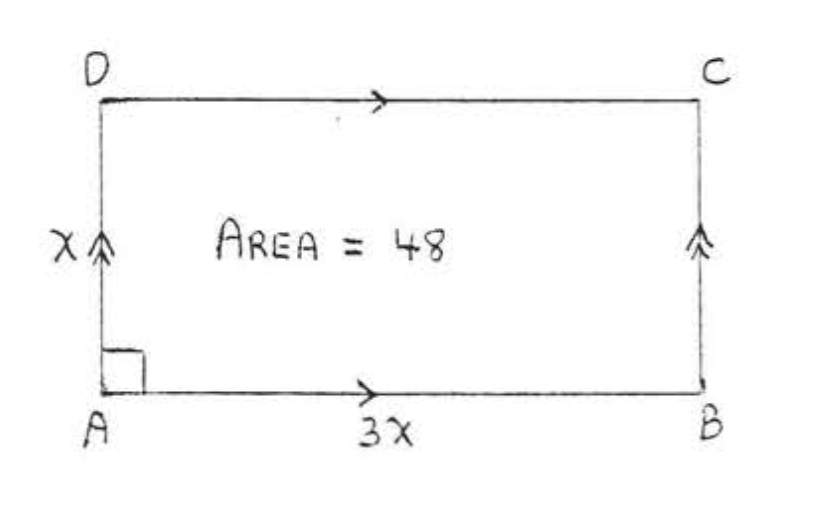
16.
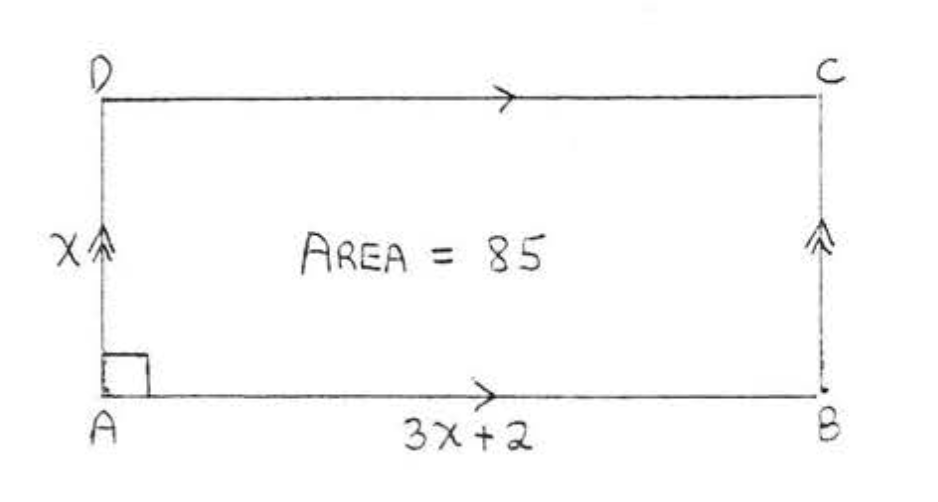
17.
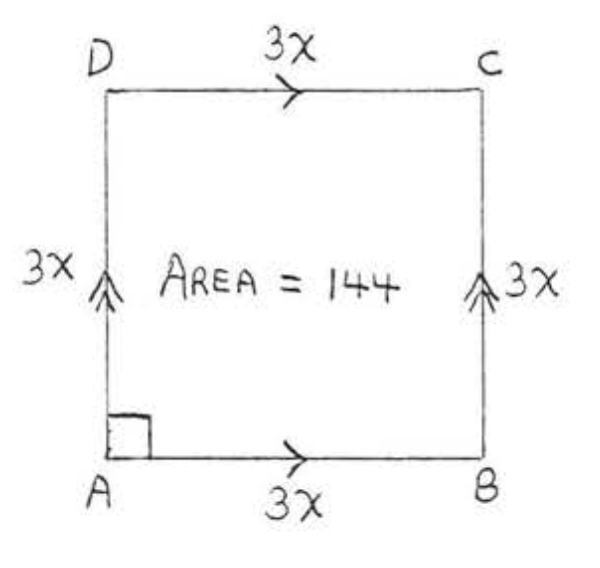
18.
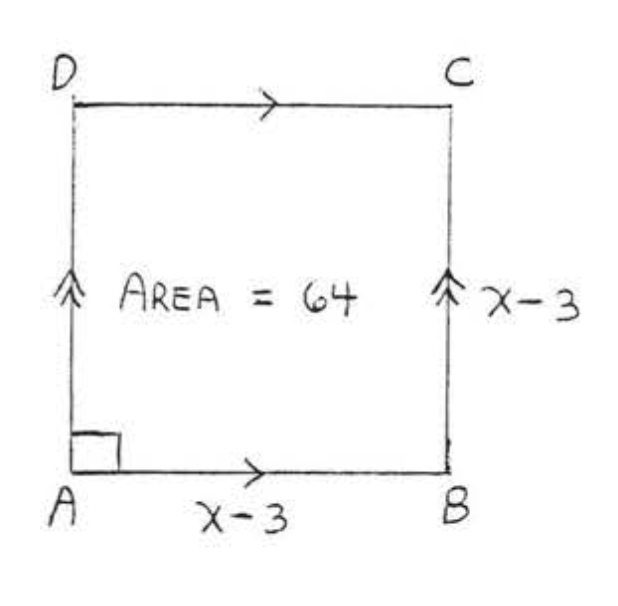
19. Un campo de fútbol tiene una longitud de 300 pies y un ancho de 160 pies. ¿Cuál es la zona?
20. Una cancha de tenis mide 78 pies de largo y 36 pies de ancho, ¿Cuál es la zona?
21 - 24. ¿Cuántas baldosas de uno por un pie se necesitan para tejear cada una de las siguientes habitaciones?
21.
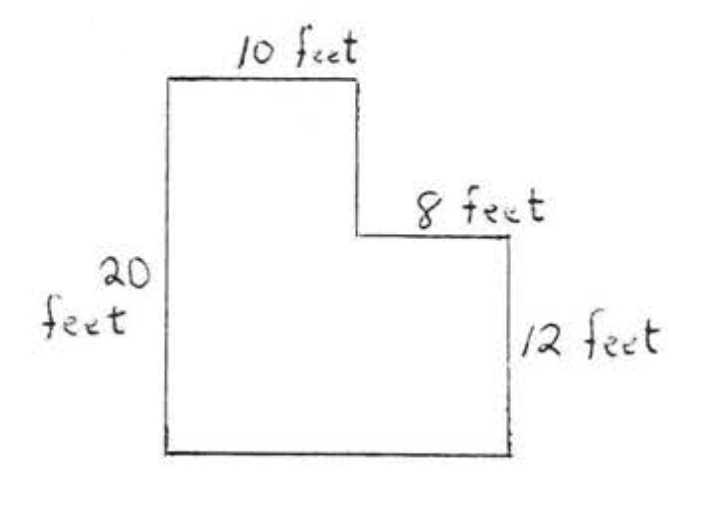
22.
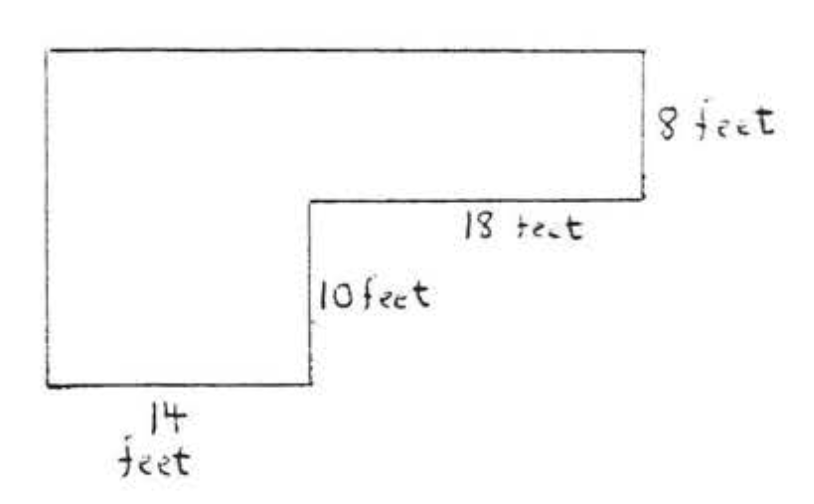
23.
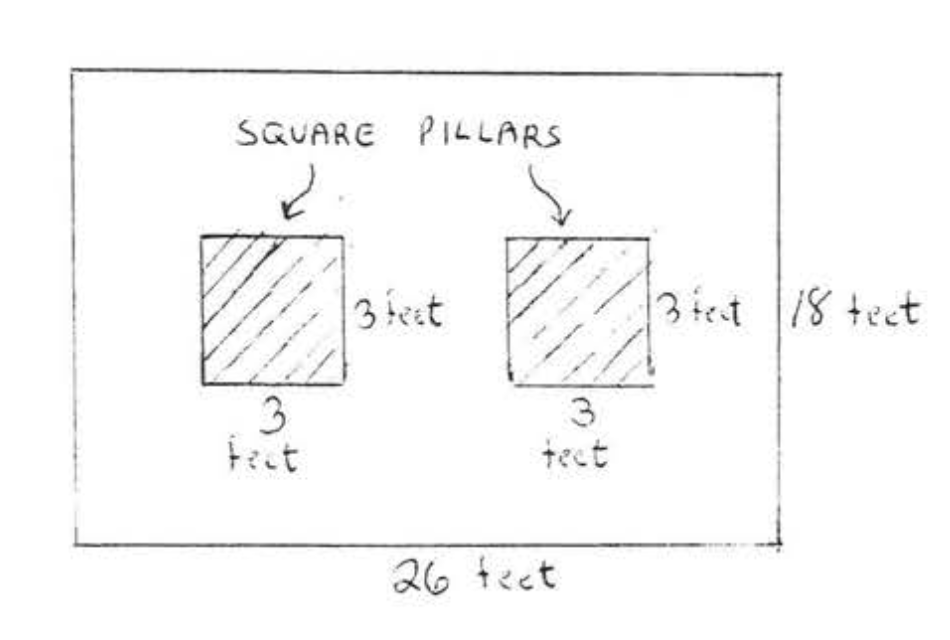
24.
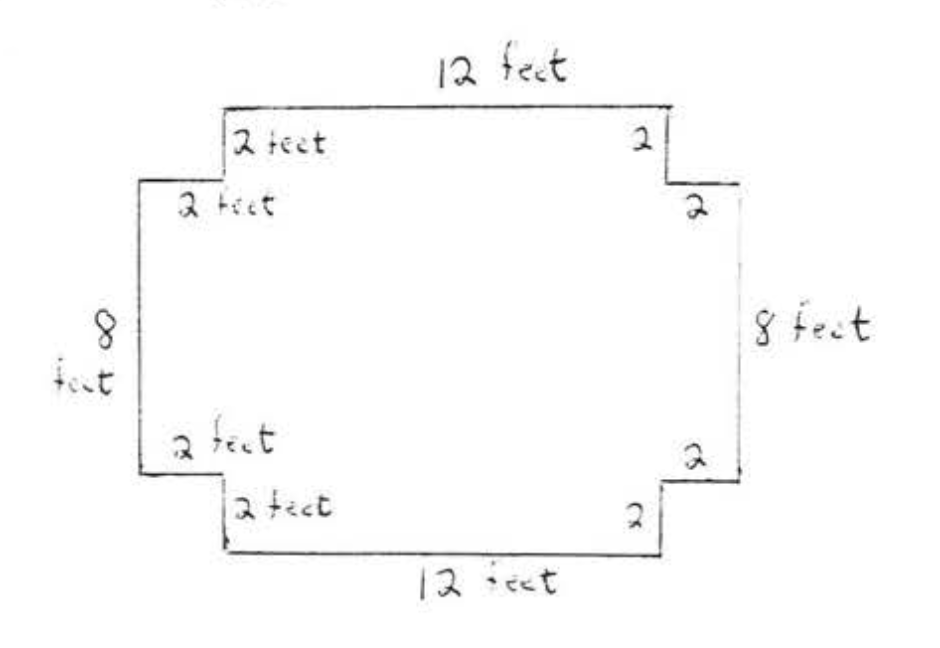
25. Una losa de concreto pesa 60 libras por pie cuadrado, ¿Cuál es el peso total de una losa rectangular de 10 pies de largo y 3 pies de ancho?
26. Una pieza rectangular de contrachapado es de 8 ey 10 pies, Si la madera contrachapada pesa 3 libras por pie cuadrado, ¿cuál es el peso de toda la pieza?


