6.5: El Área de un Trapezoide
- Page ID
- 114661
En la Figura\(\PageIndex{1}\),\(b_1\) y\(b_2\) son las bases del trapecio\(ABCD\) y\(h\) es la altura o altitud. La fórmula para el área se da en el siguiente teorema:
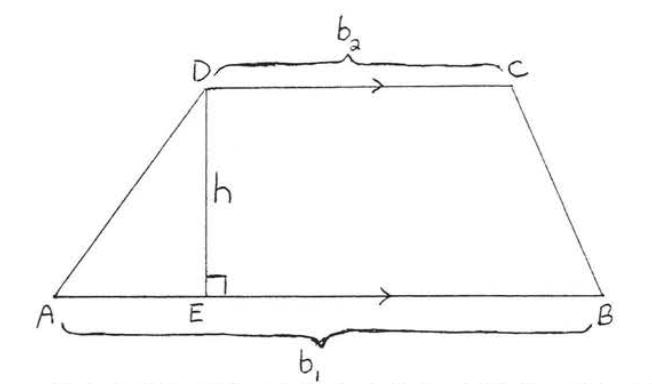
El área de un trapecio es igual a la mitad del producto de su altura y la suma de sus bases.
\[A = \dfrac{1}{2} h(b_1 + b_2)\]
- Prueba
-
En Figura\(\PageIndex{1}\) dibujar\(BD\) (ver Figura\(\PageIndex{2}\)). Tenga en cuenta que\(CD = b_2\) es la base y\(BF = h\) es la altura de\(\triangle BCD\). Área de trapecio\(ABCD =\) Área de\(\triangle ABD\) + Área de\(\triangle BCD\) =\(\dfrac{1}{2} b_1h + \dfrac{1}{2} b_2 h = \dfrac{1}{2} h(b_1 + b_2)\).
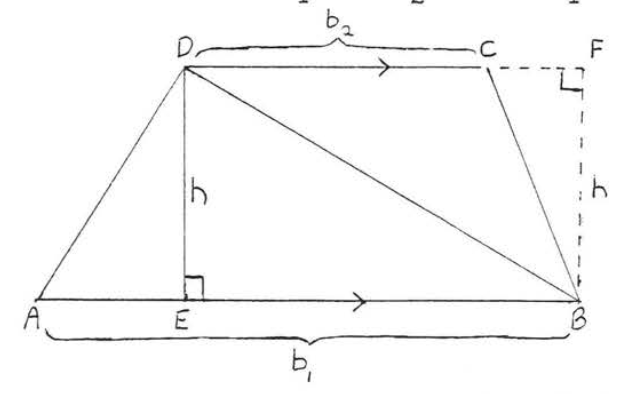
Figura\(\PageIndex{2}\): Dibujar\(BD\). \(CD\)es la base y\(BF\) es la altura de\(\triangle BCD\).
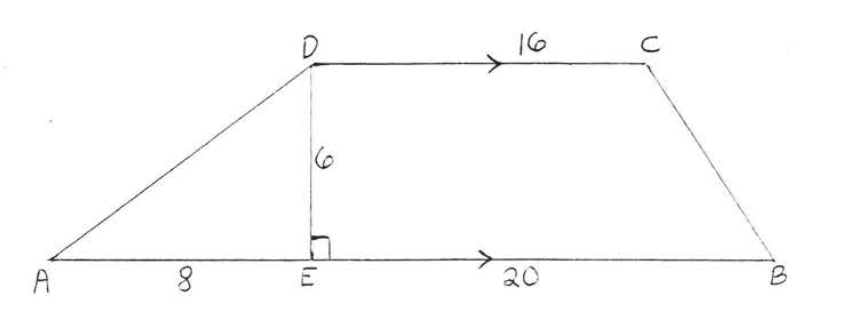
Encuentra la zona:
Solución
\(A = \dfrac{1}{2} h(b_1 + b_2)= \dfrac{1}{2} (6)(28 + 16) = \dfrac{1}{2} (6)(44) = 132\).
Respuesta:\(A = 132\).
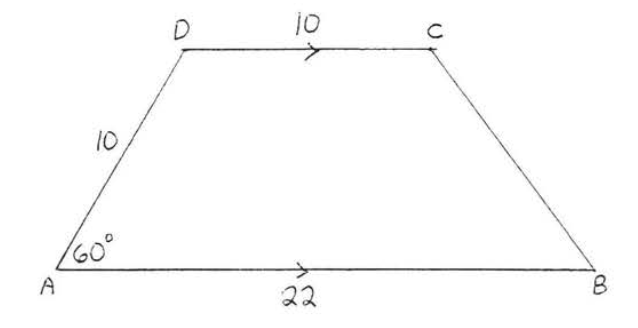
Encuentra el área y perímetro:
Solución
Dibujar alturas\(DE\) y\(CF\) (Figura\(\PageIndex{3}\)). \(\triangle ADE\)es\(30^{\circ}-60^{\circ}-90^{\circ}\) triángulo. Entonces\(AE\) = pierna corta =\(\dfrac{1}{2}\) hipotenusa =\(\dfrac{1}{2}(10) = 5\), y\(DE\) = pierna larga = (pierna corta) (\(\sqrt{3}\)) =\(5\sqrt{3}\). \(CDEF\)es un rectángulo así\(EF = CD = 10\). Por lo tanto\(BF = AB - EF = 22 -10 - 5 = 7\). Vamos\(x = BC\).
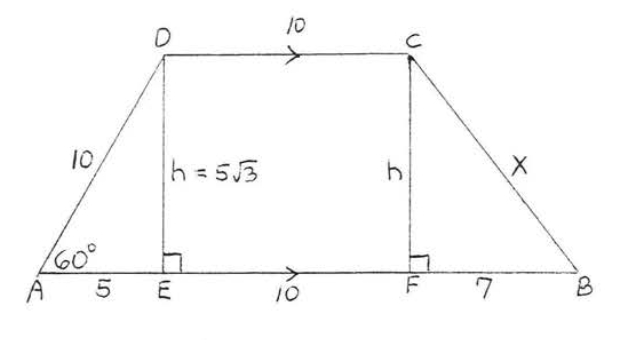
\[\begin{array} {rcl} {\text{CF}^2 + \text{BF}^2} & = & {\text{BC}^2} \\ {(5\sqrt{3})^2 + 7^2} & = & {x^2} \\ {75 + 49} & = & {x^2} \\ {124} & = & {x^2} \\ {x} & = & {\sqrt{124} = \sqrt{4} \sqrt{31} = 2\sqrt{31}} \end{array}\]
Área =\(\dfrac{1}{2} h(b_1 + b_2) = \dfrac{1}{2} (5\sqrt{3}) (22 + 10) = \dfrac{1}{2} (5\sqrt{3})(32) = 80\sqrt{3}\).
Perímetro =\(22 + 10 + 10 + 2\sqrt{31} = 42 + 2\sqrt{31}\).
Respuesta:\(A = 80\sqrt{3}\),\(P = 42 + 2\sqrt{31}\).
Problemas
1 - 2. Encuentra el área de\(ABCD\):
1.
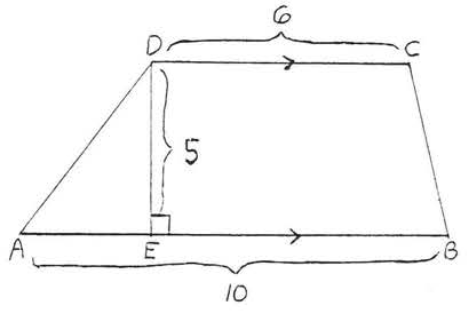
2.
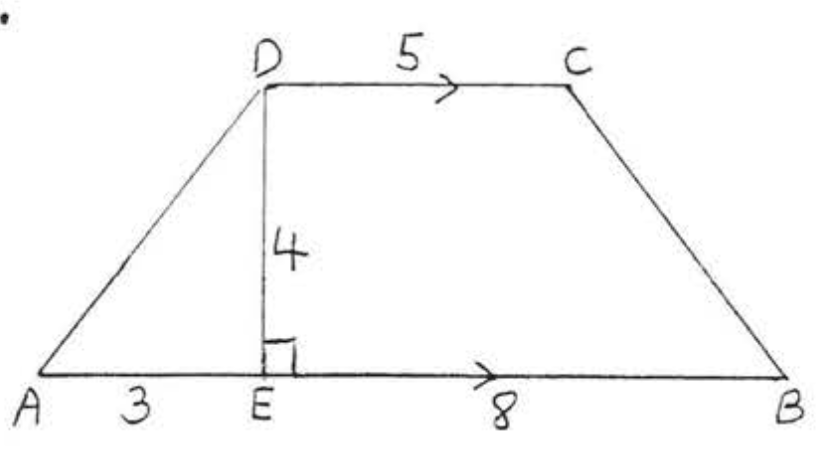
3 - 12. Encuentra el área y perímetro de\(ABCD\):
3.
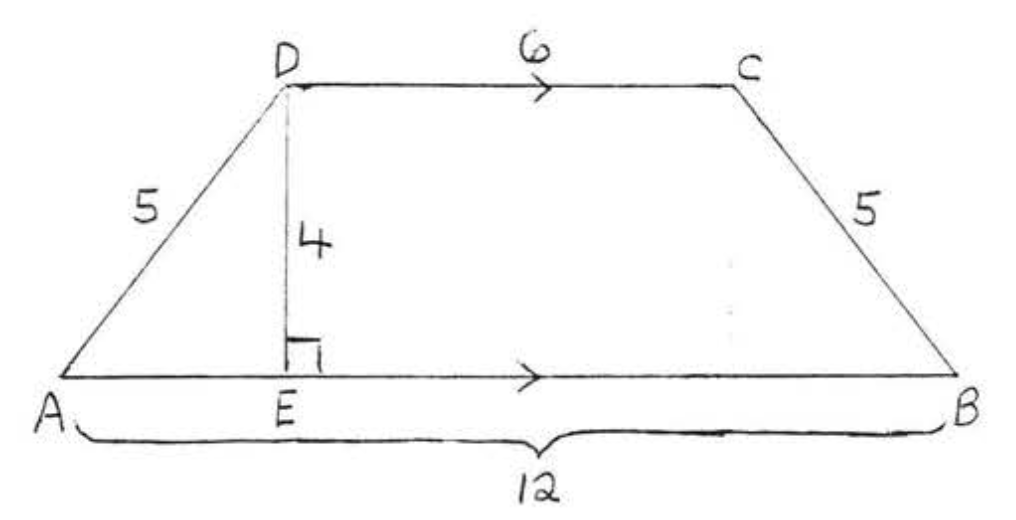
4.
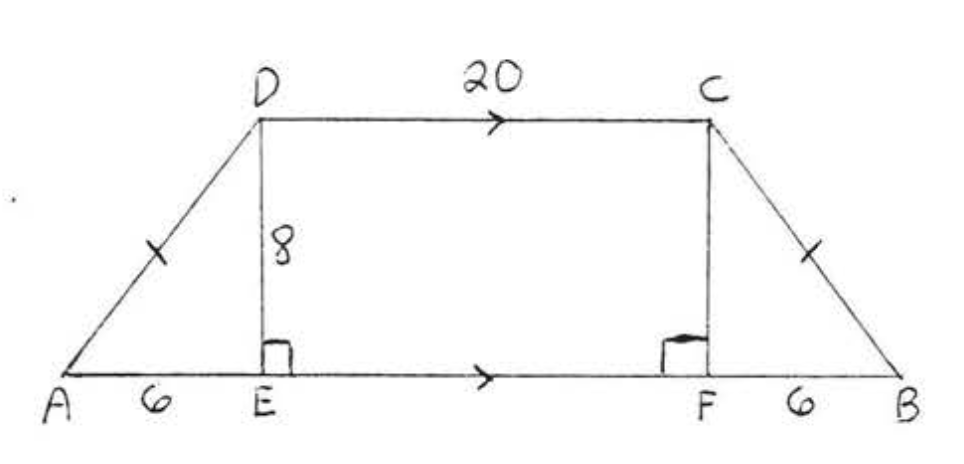
5.
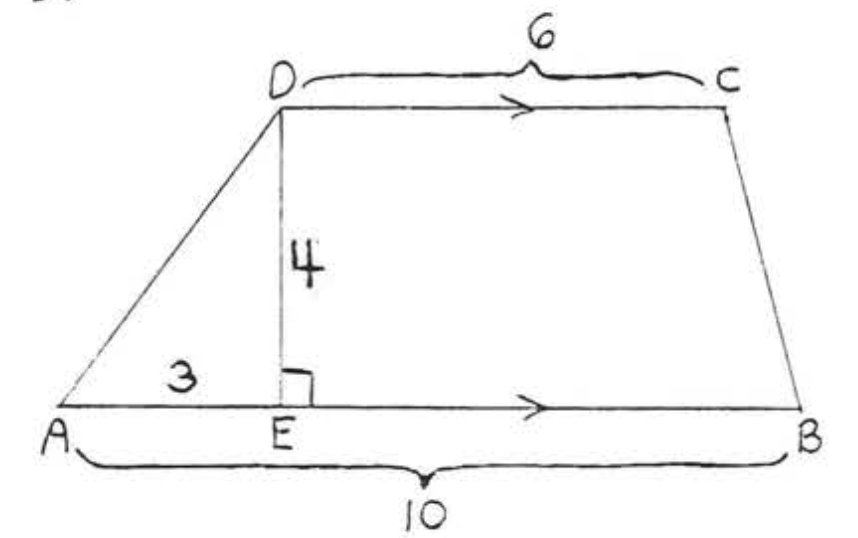
6.
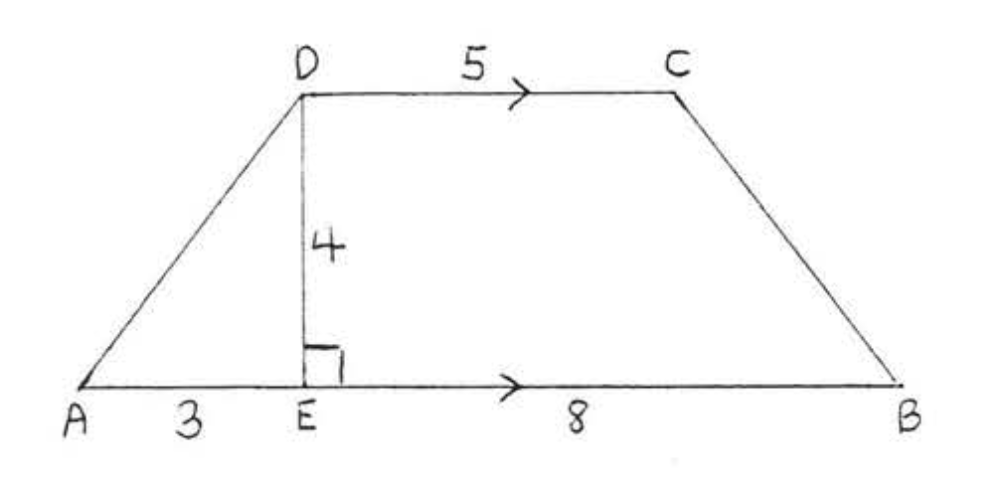
7.
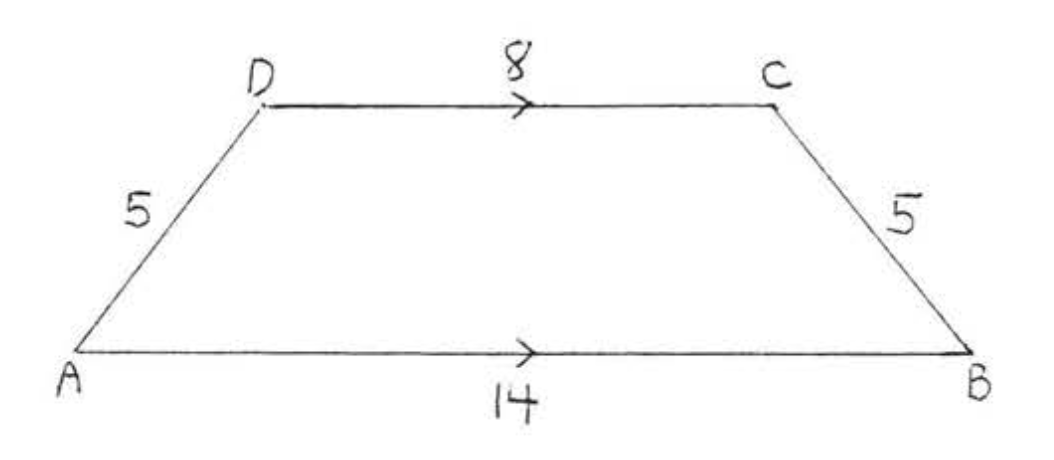
8.
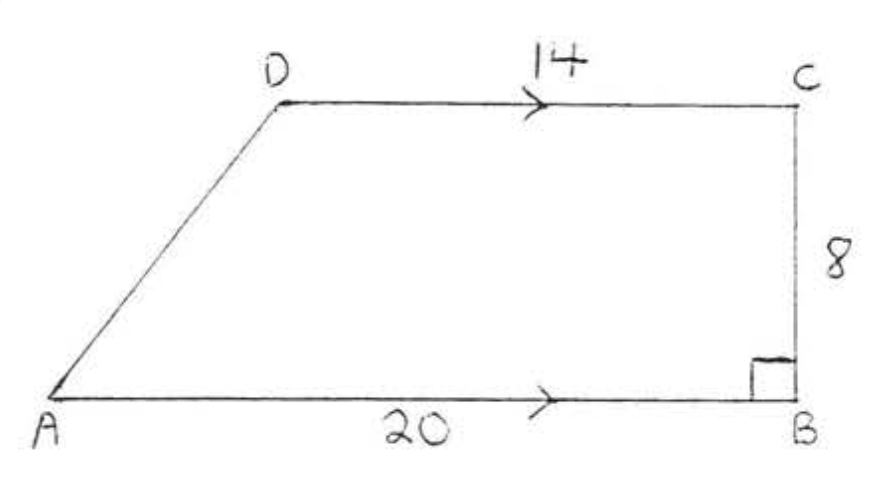
9.
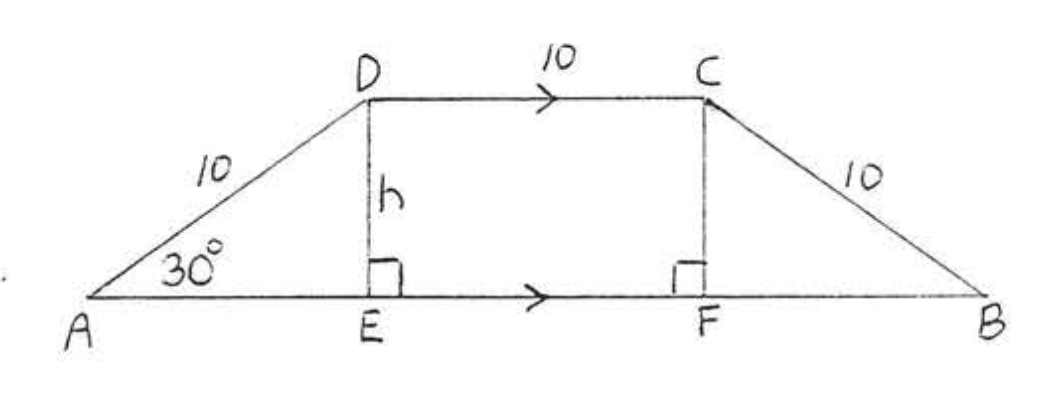
10.
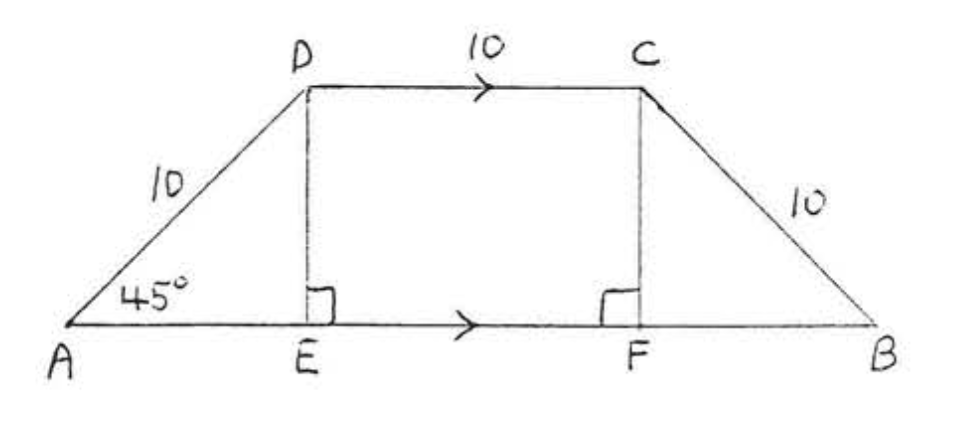
11.
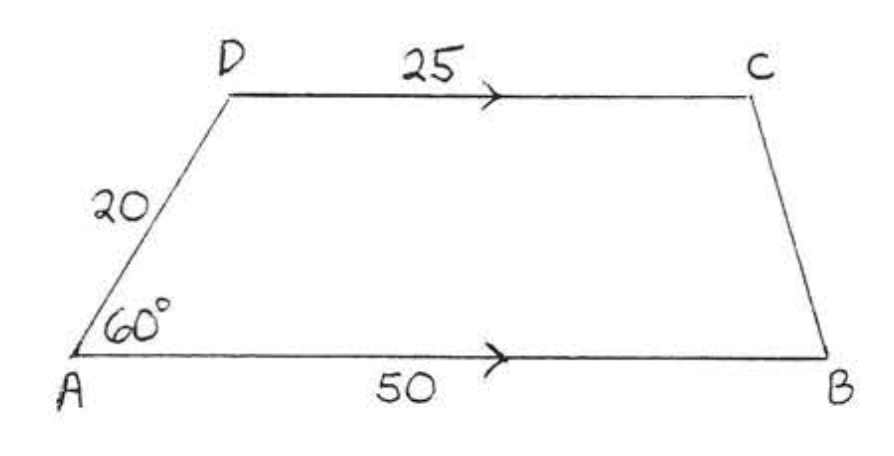
12.
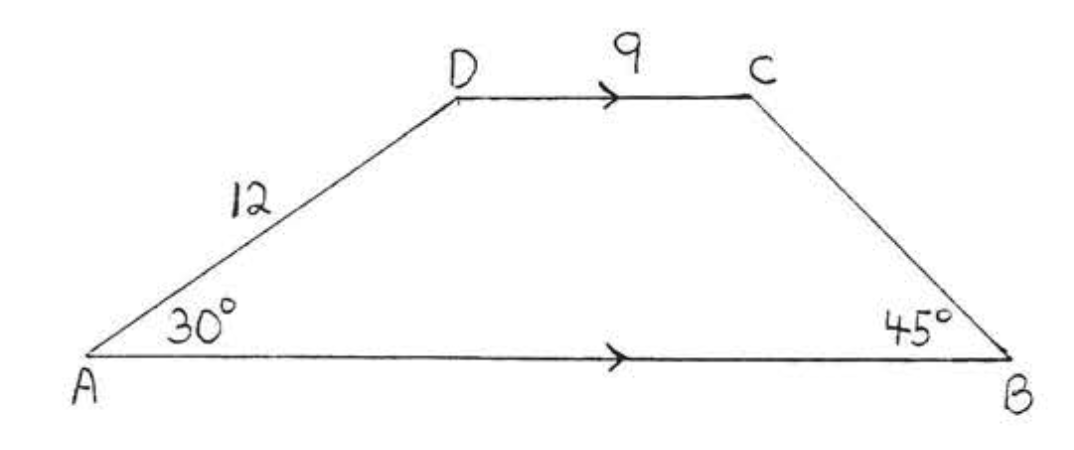
13 - 14. Encuentra el área y perímetro a la décima más cercana de\(ABCD\):
13.
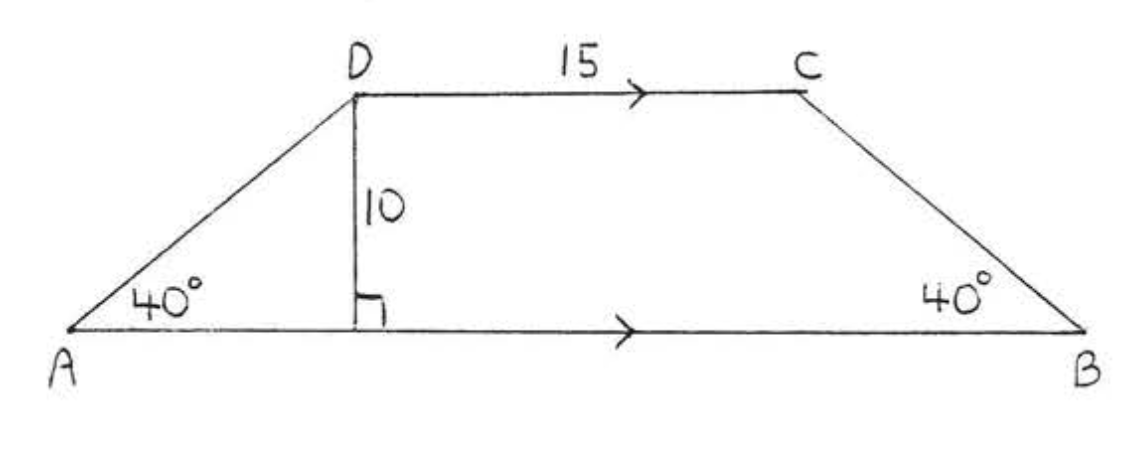
14.
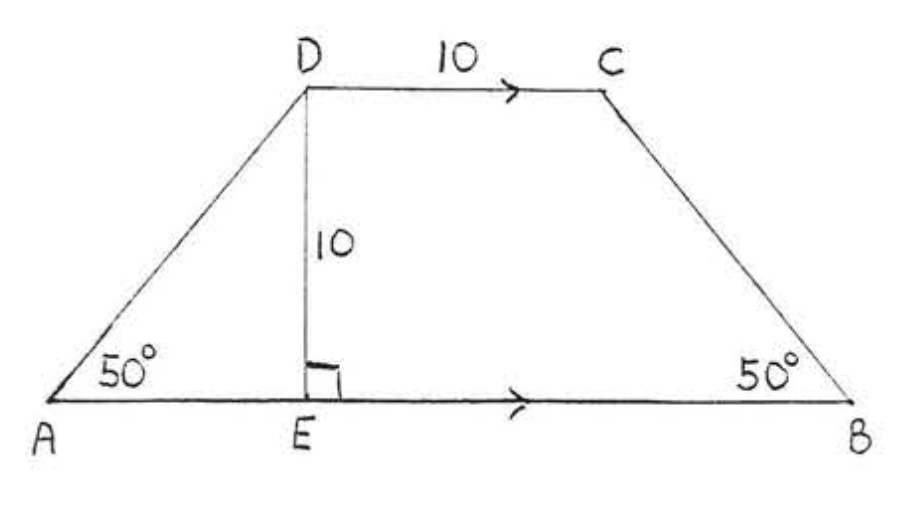
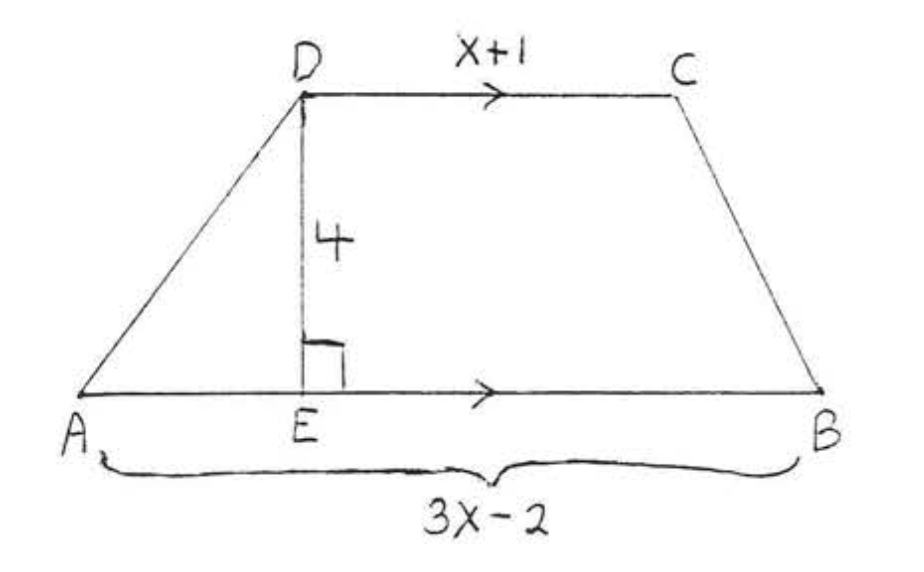
15. Encuentra\(x\) si el área de\(ABCD\) es 50:
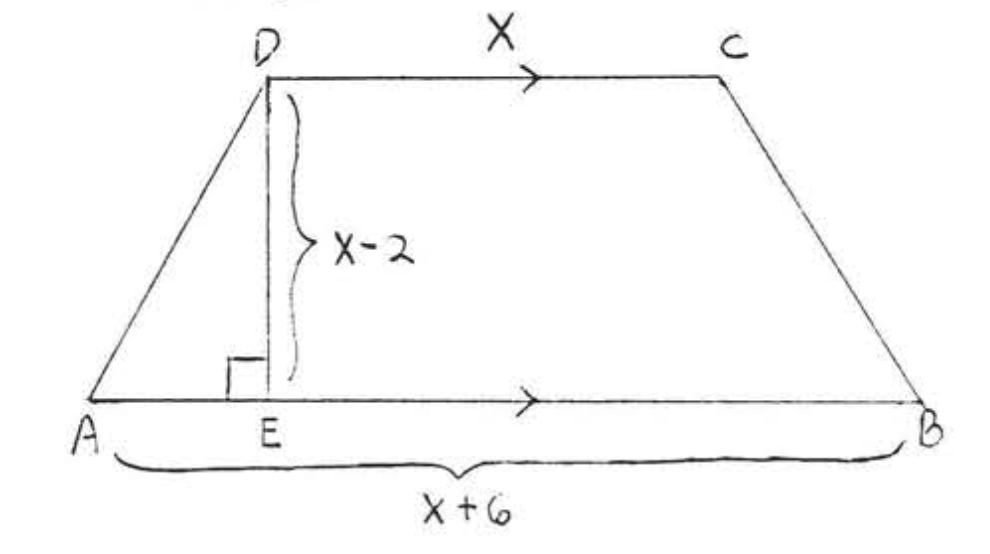
16. Encuentra\(x\) si el área de\(ABCD\) es 30: