7.1: Polígonos regulares
- Page ID
- 114761
Un polígono regular es un polígono en el que todos los lados son iguales y todos los ángulos son iguales, Ejemplos de un polígono regular son el triángulo equilátero (3 lados), el cuadrado (4 lados), el pentágono regular (5 lados) y el hexágono regular (6 lados). Los ángulos de un polígono regular se pueden encontrar fácilmente usando los métodos de la sección 1.5.
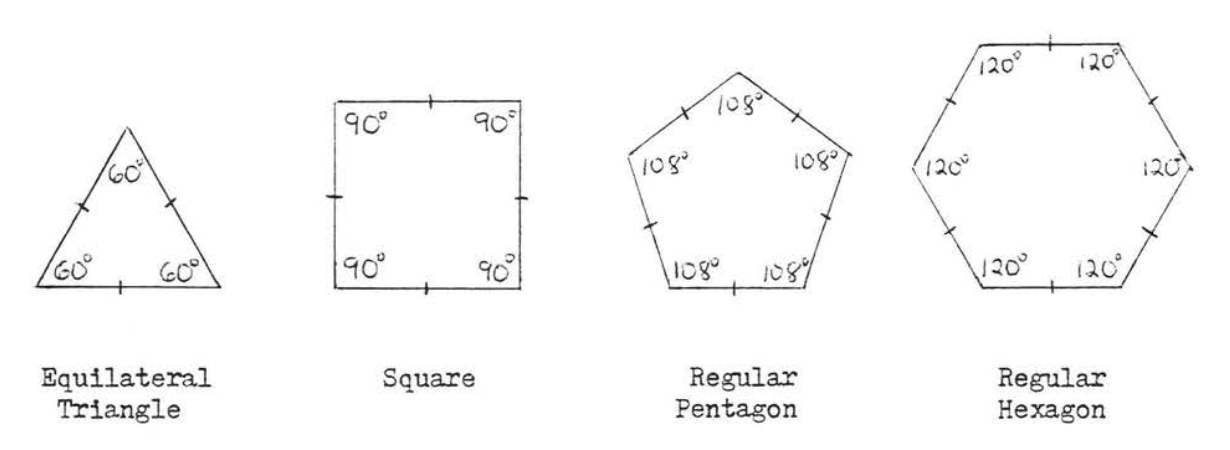
Supongamos que dibujamos el ángulo bisectriz de cada ángulo de un polígono regular, encontraremos que estos bisectores angulares se encuentran todos en el mismo punto (Figura\(\PageIndex{2}\)).
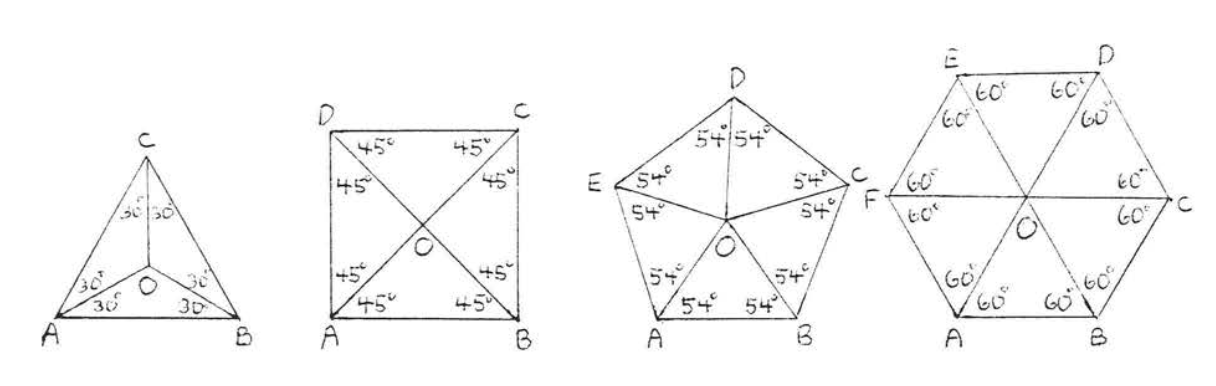
Los bisectores angulares de cada ángulo de un polígono regular se encuentran en el mismo punto. Este punto se llama el centro del polígono regular.
En la Figura\(\PageIndex{2}\). \(O\)es el centro de cada polígono regular. El segmento de cada ángulo bisectriz desde el centro hasta el vértice se denomina radio. Por ejemplo,\(OA, OB, OC, OD\), y\(OE\) son los cinco radios del pentágono regular\(ABCDE\).
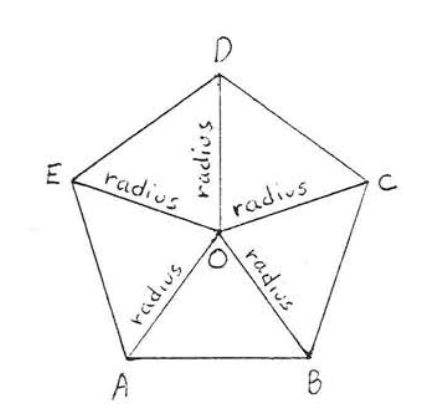
Los radios de un polígono regular dividen el polígono en triángulos isósceles congruentes. Todos los radios son iguales.
En Figura\(\PageIndex{3}\), radios\(OA, OB, OC, OD\), y\(OE\) dividir el pentágono regular en cinco triángulos isósceles con\(OA = OB =OC = OD = OE\).
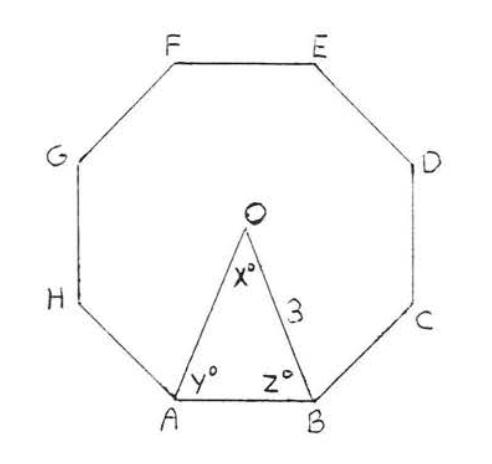
Encuentra el radio\(CA\), y los ángulos\(x^{\circ}\)\(y^{\circ}\), y\(z^{\circ}\) en el octágono regular (figura de ocho lados):
Solución
Los radios dividen el octágono en 8 triángulos isósceles congruentes. Por lo tanto\(OA = OB = 3\).
\(x^{\circ} = \dfrac{1}{8} (360^{\circ}) = 45^{\circ}\).
\(y^{\circ}= z^{\circ} = \dfrac{1}{2}(180^{\circ} - 45^{\circ}) = \dfrac{1}{2} (135^{\circ}) = 67 \dfrac{1}{2}^{\circ}\).
Respuesta:\(OA = 3, x^{\circ} = 45^{\circ}, y^{\circ} = z^{\circ} = 67 \dfrac{1}{2}^{\circ}\).
Teorema\(\PageIndex{1}\) y Teorema\(\PageIndex{2}\) parecen ser ciertos intuitivamente, pero los verificamos con una prueba formal:
Prueba de teorema\(\PageIndex{1}\) y teorema\(\PageIndex{2}\): Vamos a probar estos teoremas para el pentágono regular. La prueba para otros polígonos regulares es similar.
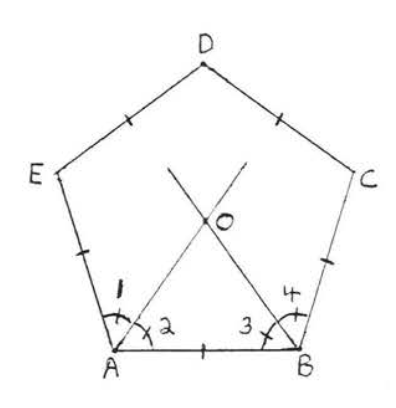
Dibuja los bisectores angulares de\(\angle A\) y\(\angle B\) como en la Figura\(\PageIndex{4}\) and call their point of intersection \(O\). We will show \(OC, OD\), and \(OE\) are the angle bisectors of \(\angle C\), \(\angle D\), and \(\angle E\) respectively.
\(\angle EAB = \angle ABC\) since the angles of a regular pentagon are equal. \(\angle 1 = \angle 2 = \dfrac{1}{2}\) of \(\angle EAB = \dfrac{1}{2}\) of \(\angle ABC = \angle 3 = \angle 4\) since \(OA\) and \(OB\) are angle bisectors.
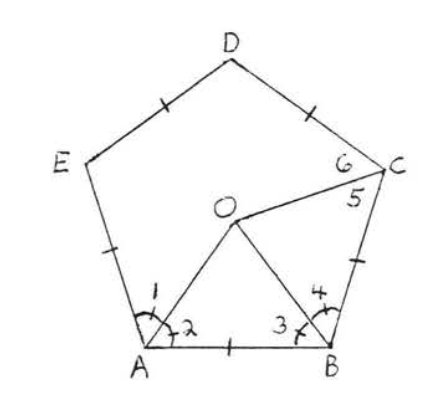
Dibujar\(OC\) (Figura\(\PageIndex{5}\)). \(AB = BC\) since the sides of a regular pentagon are equal. Therefore \(\triangle AOB \cong \triangle COB\) by \(SAS = SAS\). Therefore \(\angle 5 = \angle 2 = \dfrac{1}{2}\) of \(\angle EAB = \dfrac{1}{2}\) of \(\angle BCD\). So \(OC\) is the angle bisector of \(\angle BCD\).
De igual manera podemos mostrar bisectores\(\triangle BOC \cong \triangle DOC\), \(\triangle COD \cong \triangle EOD\), \(\triangle DOE \cong \triangle AOE\) and that \(OD\) and \(OE\) are angulares. Los triángulos son todos isósceles porque sus ángulos base son iguales. Esto completa la prueba.
Un segmento de línea dibujado desde el centro perpendicular a los lados de un polígono regular se denomina apotema (ver Figura\(PageIndex{6}\)).
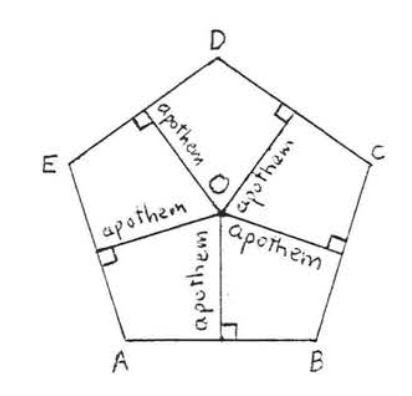
Los apotemas de un polígono regular son todos iguales, Bisectan los lados del polígono regular.
- Prueba
-
Los apotemas son todos iguales porque son las alturas de los triángulos isósceles congruentes formados por los radios (ver Teorema\(\PageIndex{2}\)), Cada apotema divide el triángulo isósceles en dos triángulos rectos congruentes, Por lo tanto cada apotema biseca un lado del polígono, que es lo que queríamos probar.
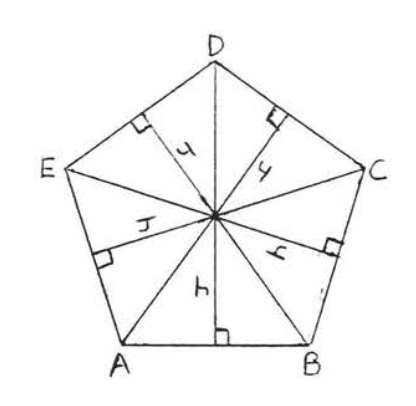
Encuentra el apotema de un pentágono regular con lado 20, a la décima más cercana.
Solución
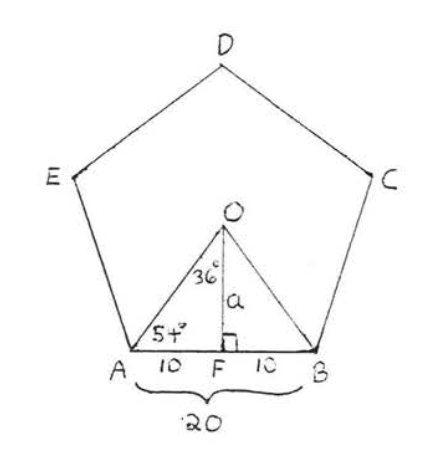
En la Figura\(\PageIndex{8}\),
\(\angle AOB = \dfrac{1}{5} (360^{\circ}) = 72^{\circ}\),
\(\angle AOF = \dfrac{1}{2}\angle AOB = \dfrac{1}{2} (72^{\circ}) = 36^{\circ}\),
y\(\angle OAF = 90^{\circ} - 36^{\circ} = 54^{\circ}\).
\(\begin{array} {rcl} {\tan 54^{\circ}} & = & {\dfrac{a}{10}} \\ {(10)1.3764} & = & {\dfrac{a}{10}(10)} \\ {13.764} & = & {a} \\ {13.8} & = & {a} \end{array}\)
Respuesta: 13.8
El apotema de un polígono regular es importante porque se utiliza para encontrar el área:
El área de un polígono regular es la mitad del producto del apotema y el perímetro.
\[A = \dfrac{1}{2} a P\]
- Prueba
-
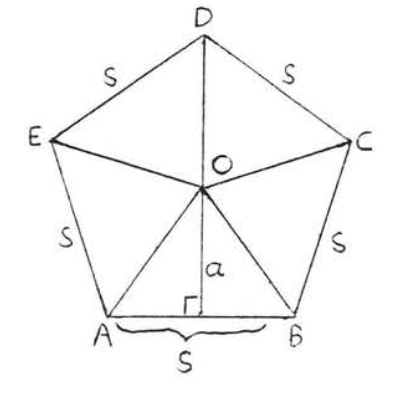
Figura\(PageIndex{9}\). El área de\(\triangle AOB\) es\(\dfrac{1}{2}\) como, donde\(s\) está el lado del pentágono. Demostramos el Teorema para el pentágono regular. La prueba para otros polígonos regulares es similar.
Los radios de un pentágono regular dividen al pentágono regular en cinco triángulos congruentes. El área de cada triángulo es\(\dfrac{1}{2}\) como, donde\(s\) está el lado del pentágono (Figura\(PageIndex{9}\)). Por lo tanto, área del pentágono = 5 (\ dfrac {1} {2} as) =\ dfrac {1} {2} a (5s) =\ dfrac {1} {2} aP\), que es la fórmula que queríamos probar.
Encuentra el área de un pentágono regular con lado 20, a la décima más cercana.
Solución
De Ejemplo\(\PageIndex{2}\) sabemos\(a = 13.764\). El perímetro\(P = (5)(20) = 100\). Por lo tanto\(A = \dfrac{1}{2} aP = \dfrac{1}{2} (13.764)(100) = \dfrac{1}{2} (1376.4) = 688.2\).
Respuesta: 688.2
Para encontrar el perímetro de un polígono regular, todo lo que tenemos que hacer es multiplicar la longitud de un lado por el número de lados. Por ejemplo, el pentágono de Figura\(\PageIndex{8}\) tiene perímetro\(P = 5(20)=100\). Sin embargo también es útil tener una fórmula para el perímetro cuando solo se conoce el radio:
El perímetro de un polígono regular de\(n\) lados con radio\(r\) viene dado por la fórmula
\[P = 2 rn \sin \dfrac{180^{\circ}}{n}\]
- Prueba
-
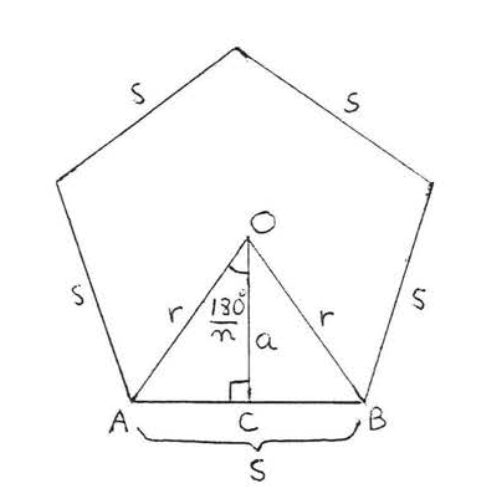
Figura\(\PageIndex{10}\): Un polígono regular con radio\(r\) y lado\(s\). Vamos a etiquetar el polígono regular como en la Figura\(PageIndex{10}\). Dado que los radios del polígono regular dividen el polígono en triángulos\(n\) congruentes (Teorema\(\PageIndex{2}\)), tenemos
\(\angle AOB = \dfrac{1}{n} (360^{\circ}) = \dfrac{360^{\circ}}{n}.\)
Por teorema el\(\PageIndex{3}\)\(OC\) apotema\(AOB\) se divide en dos triángulos rectos congruentes, así
\(\angle AOC = \dfrac{1}{2} \angle AOB = \dfrac{1}{2} (\dfrac{360^{\circ}}{n}) = \dfrac{180^{\circ}}{n}.\)
Aplicando trigonometría al triángulo rectángulo\(AOC\) tenemos
\(\begin{array} {rcl} {\sin \dfrac{180^{\circ}}{n}} & = & {\dfrac{AC}{r}} \\ {(r)\sin \dfrac{180^{\circ}}{n}} & = & {\dfrac{AC}{r} (r)} \\ {r \sin \dfrac{180^{\circ}}{n}} & = & {AC} \end{array}\)
Desde los\(OC\) bisectos\(AB\),
\(s = 2(AC)= 2r\sin \dfrac{180^{\circ}}{n}\)
y por lo tanto
\(P = ns = n(2r \sin \dfrac{180^{\circ}}{n}) = 2rn \sin \dfrac{180^{\circ}}{n}\)
que es la fórmula que deseamos probar.
Encuentra el perímetro de un pentágono regular con radio 10, a la décima más cercana.
Solución
Un pentágono tiene\(n = 5\) lados. Usando la fórmula del Teorema\(\PageIndex{5}\),\(P = 2rn \sin \dfrac{180^{\circ}}{n} = 2(10)(5) \sin \dfrac{180^{\circ}}{5} = 100 \sin 36^{\circ} = 100(.5878) = 58.78 = 58.8.\)
Respuesta: 58.8.
También puede dar fórmulas explícitas para los diversos polígonos regulares, como en la siguiente tabla:
| Figura Regular | \(n\) | \(n \sin \dfrac{180^{\circ}}{n}\) | \(P = 2 rn \sin \dfrac{180^{\circ}}{n}\) |
|---|---|---|---|
| Triángulo | \ (n\) ">3 | \ (n\ sin\ dfrac {180^ {\ circ}} {n}\) ">\(3 \sin 60^{\circ} = 2.5980\) | \ (P = 2 rn\ sin\ dfrac {180^ {\ circ}} {n}\) ">\(5.1960\ r\) |
| Cuadrado | \ (n\) ">4 | \ (n\ sin\ dfrac {180^ {\ circ}} {n}\) ">\(4 \sin 45^{\circ} = 2.8284\) | \ (P = 2 rn\ sin\ dfrac {180^ {\ circ}} {n}\) ">\(5.6568\ r\) |
| Pentágono | \ (n\) ">5 | \ (n\ sin\ dfrac {180^ {\ circ}} {n}\) ">\(5 \sin 36^{\circ} = 2.9390\) | \ (P = 2 rn\ sin\ dfrac {180^ {\ circ}} {n}\) ">\(5.8780\ r\) |
| Hexágono | \ (n\) ">6 | \ (n\ sin\ dfrac {180^ {\ circ}} {n}\) ">\(6 \sin 30^{\circ} = 3.0000\) | \ (P = 2 rn\ sin\ dfrac {180^ {\ circ}} {n}\) ">\(6.0000\ r\) |
| Decagon | \ (n\) ">10 | \ (n\ sin\ dfrac {180^ {\ circ}} {n}\) ">\(10 \sin 18^{\circ} = 3.090\) | \ (P = 2 rn\ sin\ dfrac {180^ {\ circ}} {n}\) ">\(6.180\ r\) |
| Figura de 45 lados | \ (n\) ">45 | \ (n\ sin\ dfrac {180^ {\ circ}} {n}\) ">\(45 \sin 4^{\circ} = 3.139\) | \ (P = 2 rn\ sin\ dfrac {180^ {\ circ}} {n}\) ">\(6.278\ r\) |
| Figura de 90 lados | \ (n\) ">90 | \ (n\ sin\ dfrac {180^ {\ circ}} {n}\) ">\(90 \sin 2^{\circ} = 3.141\) | \ (P = 2 rn\ sin\ dfrac {180^ {\ circ}} {n}\) ">\(6.282\ r\) |
| Figura de 1000 lados | \ (n\) ">1000 | \ (n\ sin\ dfrac {180^ {\ circ}} {n}\) ">\(1000 \sin 180^{\circ} = 3.1416\) | \ (P = 2 rn\ sin\ dfrac {180^ {\ circ}} {n}\) ">\(6.283\ r\) |
De Tabla\(\PageIndex{1}\) podemos ver que a medida que aumenta el número de lados, el perímetro de un polígono regular se vuelve aproximadamente 6.28 veces el radio. También puede reconocer que el valor de\(n \sin \dfrac{180^{\circ}}{n}\) se acerca al número\(\pi\). Volveremos a este punto cuando discutamos la circunferencia de un círculo en la sección 7.5.
Encuentra el perímetro de un pentágono regular Hith radio 10, a la décima más cercana.
Solución
De la mesa
\[ \begin{align*} P &= 5.8780\ r \\[4pt] &= 5.8780(10) \\[4pt] &= 58.78 \\[4pt] &= 58.8 \end{align*}.\]
Respuesta: 58.8.
Encuentra el apotema y el área de un pentágono regular con radio 10, a la décima más cercana.
Solución
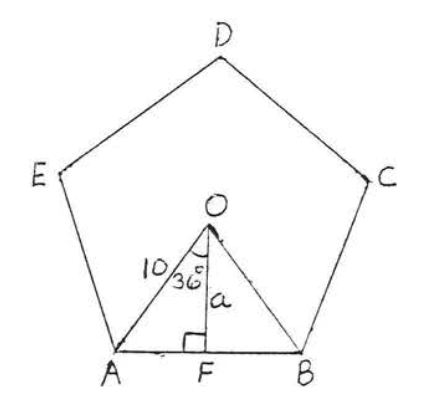
En la Figura\(\PageIndex{11}\)
\[\angle AOB = \dfrac{1}{5} (360^{\circ}) = 72^{\circ} \nonumber\]
y
\[\angle AOF = \dfrac{1}{2} \angle AOB = \dfrac{1}{2} (72^{\circ}) = 36^{\circ}. \nonumber\]
Aplicando trigonometría al triángulo rectángulo\(AOF\),
\(\begin{array} {rcl} {\cos 36^{\circ}} & = & {\dfrac{a}{10}} \\ {(10).8090} & = & {\dfrac{a}{10}(10)} \\ {8.090} & = & {a} \end{array}\)
De Ejemplo\(\PageIndex{4}\),\(P = 58.78\). Por lo tanto, por Teorema\(\PageIndex{4}\),
\(A = \dfrac{1}{2} a P = \dfrac{1}{2} (8.09) (58.78) = \dfrac{1}{2} (475.5302) = 237.7651 = 237.8.\)
Respuesta:\(a = 8.1, P = 237.8\).
En 1936 los arqueólogos desenterraron un grupo de antiguas tablas babilónicas que contenían fórmulas para las áreas de polígonos regulares de tres, cuatro, cinco, seis y siete lados, Hay evidencia de que los polígonos regulares se usaban comúnmente en la arquitectura y diseños de otras civilizaciones antiguas también, Un clásico problema de las matemáticas griegas era construir un polígono regular usando solo una regla y brújula, Los polígonos regulares generalmente se estudiaban en relación con los círculos. Como veremos más adelante en este capítulo, las fórmulas para el área y perímetro de un círculo pueden derivarse de las fórmulas correspondientes para polígonos regulares.
Problemas
1 - 6. Encuentra los ángulos\(x^{\circ}, y^{\circ}, z^{\circ}\) y el radio\(r\) de los polígonos regulares:
1.
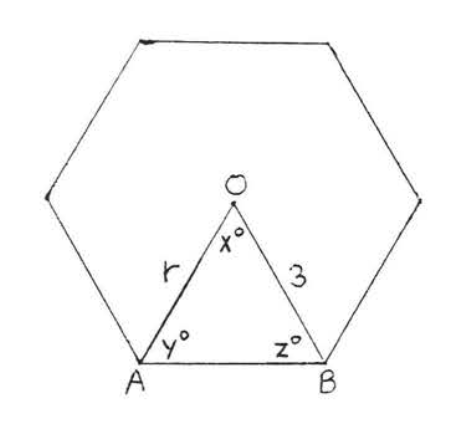
2.
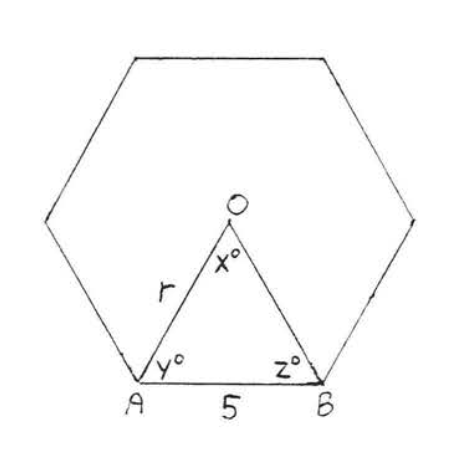
3.
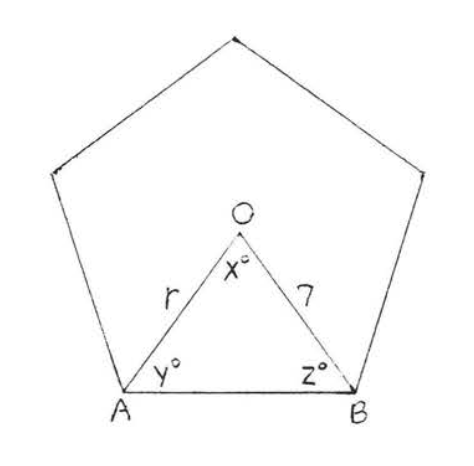
4.
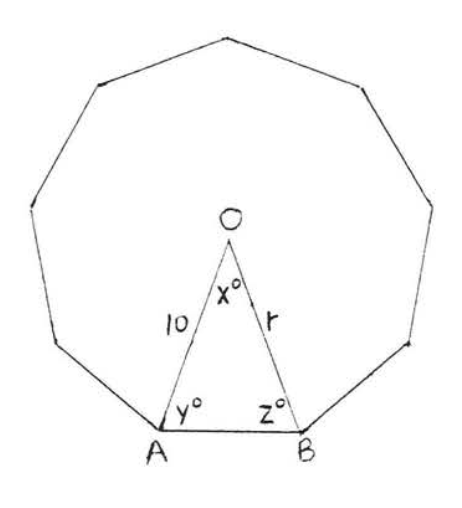
5.
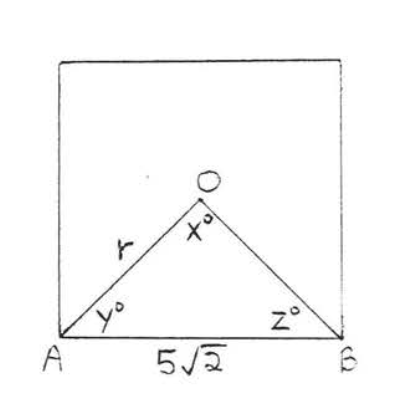
6.
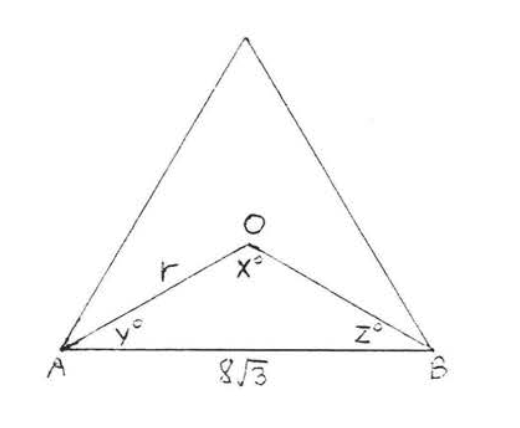
7 - 18. Encuentra el apotema, perímetro y área al décimo más cercano:
7. pentágono regular con lado 40.
8. pentágono regular con lado 16.
9. hexágono regular con lado 20.
10. hexágono regular con lado 16.
11. decagón regular (figura de diez lados) con lado 20.
12. nonagon regular (figura de nueve lados) con lado 20.
13. pentágono regular con radio 20.
14. pentágono regular con radio 5.
15. hexágono regular con radio 10.
16. hexágono regular con radio 20.
17. decagon regular con radio 10.
18. nonagon regular con radio 20.


