6.1: Sustitución

El capítulo anterior introdujo la antiderivada y la conectó a áreas firmadas bajo una curva a través del Teorema Fundamental del Cálculo. El siguiente capítulo explora más aplicaciones de integrales definidas que solo área. A medida que la evaluación de integrales definidas va a ser importante, vamos a querer encontrar antiderivados de una variedad de funciones.

Este capítulo está dedicado a explorar técnicas de antidiferenciación. Si bien no todas las funciones tienen una antiderivada en términos de funciones elementales (un concepto introducido en la sección de Integración Numérica), todavía podemos encontrar antiderivadas de una amplia variedad de funciones.

Sustitución

Motivamos esta sección con un ejemplo. Vamos\(f(x) = (x^2+3x-5)^{10}\). Podemos calcular\(f'(x)\) usando la Regla de Cadena. Se trata de:

\[f'(x) = 10(x^2+3x-5)^9\cdot(2x+3) = (20x+30)(x^2+3x-5)^9.\]

Ahora considera esto: ¿Qué es\(\int (20x+30)(x^2+3x-5)^9\ dx\)? Tenemos la respuesta frente a nosotros;

\[\int (20x+30)(x^2+3x-5)^9\ dx = (x^2+3x-5)^{10}+C.\]

¿Cómo habríamos evaluado esta integral indefinida sin comenzar\(f(x)\) como lo hicimos nosotros?

Esta sección explora la integración por sustitución. Nos permite “deshacer la regla de la cadena”. La sustitución nos permite evaluar la integral anterior sin conocer primero la función original.

El principio subyacente es reescribir una integral “complicada” de la forma\(\int f(x)\ dx\) como una integral no tan complicada\(\int h(u)\ du\). Posteriormente estableceremos formalmente cómo se hace esto. Primero, consideremos de nuevo nuestra integral introductoria indefinida,\(\int (20x+30)(x^2+3x-5)^9\ dx\). Podría decirse que la parte más “complicada” del integrando es\((x^2+3x-5)^9\). Deseamos simplificarlo; lo hacemos a través de una sustitución. Vamos\(u=x^2+3x-5\). Así

\[(x^2+3x-5)^9 = u^9.\]

Nos hemos establecido\(u\) en función de\(x\), por lo que ahora consideramos el diferencial de\(u\):

\[du = (2x+3)dx.\]

Ten en cuenta eso\((2x+3)\) y\(dx\) se multiplican; el no\(dx\) es “solo ahí sentado”.

Regresar a la integral original y hacer algunas sustituciones a través del álgebra:

\[\begin{align} \int (20x+30)(x^2+3x-5)^9\ dx &= \int 10(2x+3)(x^2+3x-5)^9\ dx \\ &=\int 10(\underbrace{x^2+3x-5}_u)^9\underbrace{(2x+3)\ dx}_{du} \\ &=\int 10u^9\ du \\ &= u^{10} + C \quad \text{(replace \(u\) with \(x^2+3x-5\))}\\ &= (x^2+3x-5)^{10} +C\end{align}\]

Uno bien podría mirar esto y pensar “Yo (algo así como) seguí cómo funcionaba eso, pero nunca se me ocurriría eso por mi cuenta”, pero el proceso es aprendible. Esta sección contiene numerosos ejemplos a través de los cuales el lector obtendrá comprensión y madurez matemática que le permitirá considerar la sustitución como una herramienta natural a la hora de evaluar integrales.

Declaramos antes que la integración por sustitución “deshace” la Regla de la Cadena. Específicamente, dejar\(F(x)\) y\(g(x)\) ser funciones diferenciables y considerar la derivada de su composición:

\[\frac{d}{dx}\Big(F\big(g(x)\big)\Big) = F'(g(x))g'(x).\]

Así

\[\int F'(g(x))g'(x)\ dx = F(g(x)) + C.\]

La integración por sustitución funciona reconociendo la función “interior”\(g(x)\) y reemplazándola por una variable. Al establecer\(u=g(x)\), podemos reescribir la derivada como

\[\frac{d}{dx}\Big(F\big(u\big)\Big) = F'(u)u'.\]

Ya que\(du = g'(x)dx\), podemos reescribir la integral anterior como

\[\int F'(g(x))g'(x)\ dx = \int F'(u) du = F(u)+C = F(g(x))+ C.\]

Este concepto es importante por lo que lo reafirmamos en el contexto de un teorema.

Teorema\(\PageIndex{1}\): Integration by Substitution

Dejar\(F\) y\(g\) ser funciones diferenciables, donde el rango de\(g\) es un intervalo\(I\) contenido en el dominio de\(F\). Entonces

\[\int F'(g(x))g'(x)\ dx = F(g(x)) + C.\]

Si\(u = g(x)\), entonces\(du = g'(x)dx\) y

\[\int F'(g(x))g'(x)\ dx = \int F'(u)\ du = F(u)+C = F(g(x))+C.\]

El punto de sustitución es facilitar el paso de integración. En efecto, el paso\(\int F'(u)\ du = F(u) + C\) parece fácil, ya que la antiderivada de la derivada de\(F\) es justa\(F\), más una constante. El “trabajo” involucrado es hacer la sustitución adecuada. No hay un proceso paso a paso que uno pueda memorizar; más bien, la experiencia será la guía de uno. Para ganar experiencia, ahora nos embarcamos en muchos ejemplos.

Ejemplo\(\PageIndex{1}\): Integrating by substitution

Evaluar\(\int x\sin(x^2+5)\ dx\).

Solución

Sabiendo que la sustitución está relacionada con la Regla de la Cadena, elegimos dejar\(u\) ser la función “interior” de\(\sin(x^2+5)\). (Esta no siempre es una buena opción, pero suele ser el mejor lugar para comenzar).

Vamos\(u = x^2+5\), de ahí\(du = 2x\,dx\). El integrando tiene un\(x\,dx\) término, pero no un\(2x\,dx\) término. (Recordemos que la multiplicación es conmutativa, por lo que el\(x\) no tiene que estar físicamente al lado\(dx\) para que haya un\(x\,dx\) término.) Podemos dividir ambos lados de la\(du\) expresión por 2:

\[du = 2x\,dx \quad \Rightarrow \quad \frac12du = x\,dx.\]

Ahora podemos sustituir.

\[\begin{align}\int x\sin(x^2+5)\ dx &= \int \sin(\underbrace{x^2+5}_u) \underbrace{x\ dx}_{\frac12du}\\ &= \int \frac12\sin u\ du\end{align}\]

\[\begin{align} \phantom{\int x\sin(x^2+5)\ dx} &= -\frac12\cos u + C \quad \text{ (now replace \(u\) with \(x^2+5\))}\\ &=-\frac12\cos(x^2+5) + C. \end{align}\]

Así\(\int x\sin(x^2+5)\ dx = -\frac12\cos(x^2+5)+C\). Podemos verificar nuestro trabajo evaluando la derivada del lado derecho.

Ejemplo\(\PageIndex{2}\): Integrating by substitution

Evaluar\(\int \cos(5x)\ dx\).

Solución

Nuevamente vamos a\(u\) reemplazar la función “inside”. Dejando\(u = 5x\), tenemos\(du = 5dx\). Dado que nuestro integrando no tiene\(5dx\) término, podemos dividir la ecuación anterior por\(5\) para obtener\(\frac15du = dx\). Ahora podemos sustituir.

\[\begin{align} \int \cos(5x)\ dx &= \int \cos(\underbrace{5x}_u) \underbrace{dx}_{\frac15du} \\&= \int \frac15\cos u \ du \\ &= \frac15\sin u + C \\&= \frac15\sin (5x)+C. \end{align}\]

Podemos volver a comprobar nuestro trabajo a través de la diferenciación.

El ejemplo anterior exhibió un tipo de sustitución común y simple. La función “inside” era una función lineal (en este caso,\(y = 5x\)). Cuando la función interna es lineal, la integración resultante es muy predecible, se describe aquí.

Idea Clave 10: Sustitución con una Función Lineal

Considerar\(\int F'(ax+b)\ dx\), dónde\(a\neq 0\) y\(b\) son constantes. Dejar\(u = ax+b\) da\(du = a\cdot dx\), llevando al resultado

\[\int F'(ax+b)\ dx = \frac{1}{a}F(ax+b) + C.\]

Así\(\int \sin (7x-4)\ dx = -\frac17\cos(7x-4)+C\). Nuestro siguiente ejemplo puede usar Key Idea 10, pero solo la emplearemos después de pasar por todos los pasos.

Ejemplo\(\PageIndex{3}\): Integrating by substituting a linear function

Evaluar\(\int \frac{7}{-3x+1}\ dx\).

Solución

Ver esto una composición de funciones\(f(g(x))\), dónde\(f(x) = 7/x\) y\(g(x) = -3x+1\). Empleando nuestra comprensión de la sustitución, dejamos\(u = -3x+1\), la función interna. Así\(du = -3dx\). El integrando carece de a\(-3\); de ahí dividir la ecuación anterior por\(-3\) para obtener\(-du/3 = dx\). Ahora podemos evaluar la integral a través de la sustitución.

\[\begin{align} \int \frac{7}{-3x+1}\ dx &= \int \frac{7}{u}\frac{du}{-3} \\ &= \frac{-7}3\int \frac{du}{u} \\ &= \frac{-7}3\ln |u| + C\\ &=-\frac73\ln|-3x+1| + C. \end{align}\]

Usar Key Idea 10 es más rápido, reconociendo que\(u\) es lineal y\(a = -3\). Es posible que uno quiera seguir escribiendo todos los pasos hasta que se sientan cómodos con este atajo en particular.

No todas las integrales que se benefician de la sustitución tienen una clara función “interna”. Varios de los siguientes ejemplos demostrarán formas en que esto ocurre.

Ejemplo\(\PageIndex{4}\): Integrating by substitution

Evaluar\(\int \sin x\cos x\ dx\).

Solución

Aquí no hay una composición de función para explotar; más bien, solo un producto de funciones. No tengas miedo de experimentar; cuando se le da una integral para evaluar, muchas veces es beneficioso pensar “Si dejo\(u\) ser esto, entonces\(du\) debe ser eso...” y ver si esto ayuda a simplificar en absoluto la integral.

En este ejemplo, vamos a establecer\(u = \sin x\). Entonces\(du = \cos x\ dx\), ¡que tenemos como parte del integrand! La sustitución se vuelve muy sencilla:

\[ \begin{align} \int \sin x\cos x\ dx &= \int u\ du \\ &= \frac12u^2+ C \\ &= \frac12\sin^2 x + C. \end{align}\]

Uno haría bien en preguntar “¿Qué pasaría si lo dejamos\(u = \cos x\)?” El resultado es igual de fácil de encontrar, pero se ve muy diferente. El reto para el lector es evaluar el dejar integral\(u = \cos x\) y descubrir por qué la respuesta es la misma, pero se ve diferente.

Nuestros ejemplos hasta ahora han requerido “sustitución básica”. El siguiente ejemplo demuestra cómo se pueden hacer sustituciones que a menudo golpean al nuevo alumno como “no estándar”.

Ejemplo\(\PageIndex{5}\): Integrating by substitution

Evaluar\(\int x\sqrt{x+3}\ dx\).

Solución

Reconociendo la composición de funciones, conjunto\(u = x+3\). Entonces\(du = dx\), dando lo que inicialmente parece ser una simple sustitución. Pero en esta etapa, tenemos:

\[\int x\sqrt{x+3}\ dx = \int x\sqrt{u}\ du.\]

No podemos evaluar una integral que tenga tanto una\(x\) como una\(u\) en ella. Necesitamos convertir el\(x\) a una expresión que involucre solo\(u\).

Desde que nos fijamos\(u = x+3\), también podemos afirmar eso\(u-3 = x\). Así podemos sustituir\(x\) en el integrando con\(u-3\). También será útil reescribir\(\sqrt{u}\) como\(u^\frac12\).

\[\begin{align} \int x\sqrt{x+3} \ dx &= \int (u-3)u^\frac12\ du \\ &= \int \big(u^\frac32 - 3u^\frac12\big) \ du \\ &= \frac25u^\frac52 - 2u^\frac32 + C \\ &= \frac25(x+3)^\frac52 - 2(x+3)^\frac32 + C.\end{align}\]

Revisar tu trabajo siempre es una buena idea. En este caso particular, se necesitará algo de álgebra para hacer que la respuesta de uno coincida con el integrando en el problema original.

Ejemplo\(\PageIndex{6}\): Integrating by substitution

Evaluar\(\int \frac{1}{x\ln x}\ dx\).

Solución

Este es otro ejemplo donde no parece haber una composición obvia de funciones. La línea de pensamiento utilizada en Ejemplo\(\PageIndex{5}\) es útil aquí: elegir algo para\(u\) y considerar lo que esto implica\(du\) debe ser. Si se\(u\) puede elegir tal que\(du\) también aparece en el integrando, entonces hemos elegido bien.

Elegir\(u = 1/x\) hace\(du = -1/x^2\ dx\); eso no parece útil. Sin embargo, el ajuste\(u = \ln x\) hace\(du = 1/x\ dx\), que es parte del integrando. Así:

\[\begin{align} \int \frac1{x\ln x}\ dx &= \int \frac{1}{\underbrace{\ln x}_{1/u}}\underbrace{\frac1x\ dx}_{du} \\ &= \int \frac1u\ du \\ &= \ln |u| + C \\ &= \ln | \ln x| + C.\end{align}\]

La respuesta final es interesante; el tronco natural del tronco natural. Toma la derivada para confirmar que esta respuesta es efectivamente correcta.

Integrales que involucran funciones trigonométricas

La sección 6.3 profundiza en las integrales de una variedad de funciones trigonométricas; aquí utilizamos la sustitución para establecer una base sobre la que construiremos.

Los siguientes tres ejemplos ayudarán a llenar algunas piezas faltantes de nuestro conocimiento antiderivado. Conocemos las antiderivadas de las funciones seno y coseno; ¿qué pasa con las otras funciones estándar tangente, cotangente, secante y cosecante? Los descubrimos a continuación.

Ejemplo\(\PageIndex{7}\): Integration by substitution: antiderivatives of \(\tan x\)

Evaluar\(\int \tan x\ dx.\)

Solución

El párrafo anterior establecía que no conocíamos los antiderivados de la tangente, de ahí que debemos asumir que hemos aprendido algo en esta sección que puede ayudarnos a evaluar esta integral indefinida.

Reescribir\(\tan x\) como\(\sin x/\cos x\). Si bien la presencia de una composición de funciones puede no ser inmediatamente obvia, reconozca que\(\cos x\) está “dentro” de la\(1/x\) función. Por lo tanto, vemos si la configuración\(u = \cos x\) devuelve resultados utilizables. Tenemos eso\(du = -\sin x\ dx\), de ahí\(-du = \sin x\ dx\). Podemos integrar:

\[\begin{align}\int \tan x \ dx &= \int \frac{\sin x}{\cos x}\ dx \\ &= \int \frac1{\underbrace{\cos x}_u}\underbrace{\sin x\ dx}_{-du} \\ &= \int \frac {-1}u \ du\\ &= -\ln |u| + C \\ &= -\ln |\cos x| + C.\end{align}\]

Algunos textos prefieren traer el\(-1\) interior del logaritmo como una potencia de\(\cos x\), como en:

\[\begin{align} -\ln |\cos x| + C &= \ln |(\cos x)^{-1}| + C\\ &= \ln \left| \frac{1}{\cos x}\right| + C\\&= \ln |\sec x| + C.\end{align}\]

Así el resultado que dan es\(\int \tan x \ dx = \ln|\sec x| + C\). Estas dos respuestas son equivalentes.

Ejemplo\(\PageIndex{8}\): Integrating by substitution: antiderivatives of \(\sec x\)

Evaluar\(\int \sec x\ dx\).

Solución

Este ejemplo emplea un truco maravilloso: multiplicar el integrando por “1" para que veamos cómo integrar más claramente. En este caso, escribimos “1" como

\[1 = \frac{\sec x + \tan x}{\sec x + \tan x}.\]

Esto puede parecer que salió del campo izquierdo, pero funciona maravillosamente. Considerar:

\[\begin{align} \int \sec x\ dx &= \int \sec x\cdot \frac{\sec x + \tan x}{\sec x + \tan x}\ dx \\ &= \int \frac{\sec^2 x + \sec x\tan x}{\sec x + \tan x}\ dx.\end{align}\]

Ahora vamos\(u = \sec x+\tan x\); esto significa\(du = (\sec x\tan x+ \sec^2 x)\ dx\), que es nuestro numerador. Así:

\[\begin{align} &= \int \frac{du}{u} \\ &= \ln |u| + C \\ &= \ln |\sec x+\tan x| + C.\end{align}\]

Podemos utilizar técnicas similares a las utilizadas en los Ejemplos\(\PageIndex{6}\) y\(\PageIndex{7}\) para encontrar antiderivados de\(\cot x\) y\(\csc x\) (que el lector puede explorar en los ejercicios). Resumimos nuestros resultados aquí.

Teorema\(\PageIndex{1}\): Antiderivatives of Trigonometric Functions

1. \( \int \sin x \ dx = -\cos x +C\)
2. \(\int \cos x\ dx = \sin x + C\)
3. \(\int \tan x\ dx = -\ln|\cos x|+C\)
4. \( \int \csc x \ dx = -\ln|\csc x+\cot x| +C\)
5. \(\int \sec x\ dx = \ln|\sec x+\tan x| + C\)
6. \( \int \cot x\ dx = \ln|\sin x|+C\)

Exploramos una integral trigonométrica más común.

Ejemplo\(\PageIndex{9}\): Integration by substitution: powers of \(\cos x\) and \(\sin x\)

Evaluar\(\int \cos^2x\ dx\).

Solución

Tenemos una composición de funciones como\(\cos^2x = \big(\cos x\big)^2\).

No obstante, establecer\(u = \cos x\) significa\(du = -\sin x\ dx\), que no tenemos en la integral. Se necesita otra técnica.

El proceso que vamos a emplear es utilizar una fórmula de reducción de potencia para\(\cos^2x\) (quizás consultar el reverso de este texto para esta fórmula), que establece

\[\cos ^2x = \frac{1+\cos(2x)}{2}.\]

El lado derecho de esta ecuación no es difícil de integrar. Contamos con:

\[\begin{align} \int \cos^2x\ dx &= \int \frac{1+\cos(2x)}2\ dx \\ &= \int \left( \frac12 + \frac12\cos(2x)\right)\ dx. \end{align} \]

Ahora usa Key Idea 10:

\[\begin{align} &= \frac12x + \frac12\frac{\sin(2x)}{2} + C\\&= \frac12x + \frac{\sin(2x)}4 + C.\end{align}\]

Haremos un uso significativo de esta técnica de reducción de potencia en futuras secciones.

Simplificando el Integrand

Es común ser reacios a manipular el integrando de una integral; al principio, nuestra comprensión de la integración es tenue y uno puede pensar que trabajar con el integrando cambiará indebidamente los resultados. La integración por sustitución funciona usando una lógica diferente: mientras se mantenga la igualdad, el integrando puede ser manipulado para que su forma sea más fácil de tratar. Los siguientes dos ejemplos demuestran formas comunes en las que el uso del álgebra primero hace que la integración sea más fácil de realizar.

Ejemplo\(\PageIndex{10}\): Integration by substitution: simplifying first

Evaluar\(\displaystyle \int \frac{x^3+4x^2+8x+5}{x^2+2x+1}\ dx\).

Solución

Se puede intentar comenzar estableciendo\(u\) igual al numerador o denominador; en cada instancia, el resultado no es viable.

Cuando se trata de funciones racionales (es decir, cocientes formados por funciones polinómicas), es una regla casi universal que todo funcione mejor cuando el grado del numerador es menor que el grado del denominador. De ahí que se utilice la división polinómica.

Nos saltamos los detalles de los pasos, pero tenga en cuenta que cuando\(x^2+2x+1\) se divide en\(x^3+4x^2+8x+5\), va en\(x+2\) tiempos con un resto de\(3x+3\). Así

\[\frac{x^3+4x^2+8x+5}{x^2+2x+1} = x+2 + \frac{3x+3}{x^2+2x+1}.\]

Integrar\(x+2\) es simple. La fracción se puede integrar ajustando\(u = x^2+2x+1\), dando\(du = (2x+2)\ dx\). Esto es muy similar al numerador. Tenga en cuenta que\(du/2 = (x+1)\ dx\) y luego considere lo siguiente:

\[\begin{align}\int \frac{x^3+4x^2+8x+5}{x^2+2x+1}\ dx & = \int \left(x+2 + \frac{3x+3}{x^2+2x+1}\right)\ dx \\ &= \int (x+2)\ dx + \int \frac{3(x+1)}{x^2+2x+1}\ dx \\ & = \frac12x^2+2x+C_1 + \int \frac{3}{u}\frac{du}{2} \\ &= \frac12x^2+2x+C_1 + \frac32\ln|u| + C_2 \\&= \frac12x^2+2x+\frac32\ln|x^2+2x+1| + C.\end{align}\]

De alguna manera, “tuvimos suerte” en que después de dividir, se pudo hacer la sustitución. En secciones posteriores desarrollaremos técnicas para el manejo de funciones racionales donde la sustitución no sea directamente factible.

Ejemplo\(\PageIndex{11}\): Integration by alternate methods

Evaluar\(\displaystyle \int \frac{x^2+2x+3}{\sqrt{x}}\ dx\) con y sin sustitución.

Solución

Ya sabemos integrar este ejemplo en particular. Reescribe\(\sqrt{x}\) como\(x^\frac12\) y simplificar la fracción:

\[ \frac{x^2+2x+3}{x^{1/2}} = x^\frac32 + 2x^\frac12 + 3x^{-\frac12}.\]

Ahora podemos integrarnos usando la Regla de Poder:

\[\begin{align} \int \frac{x^2+2x+3}{x^{1/2}}\ dx &= \int\left(x^\frac32 + 2x^\frac12 + 3x^{-\frac12}\right)\ dx\\ &= \frac25x^\frac52 + \frac43x^\frac32 + 6x^\frac12 + C\end{align}\]

Este es un enfoque perfectamente fino. Demostramos cómo esto también se puede resolver usando la sustitución ya que su implementación es bastante inteligente.

Dejar\(u = \sqrt{x} = x^\frac12\); por lo tanto

\ [du =\ frac12x^ {-\ frac12} dx =\ frac {1} {2\ sqrt {x}}\ dx\ quad\ Rightarrow\ quad 2du =\ frac {1} {\ sqrt {x}}\ dx. $$

Esto nos da\(\displaystyle \int \frac{x^2+2x+3}{\sqrt{x}}\ dx = \int (x^2+2x+3)\cdot2\ du\). ¿Qué vamos a hacer con los otros\(x\) términos? Ya que\(u = x^\frac12\)\(u^2 = x\),, etc. podemos entonces sustituir\(x^2\) y\(x\) con los poderes apropiados de\(u\). Por lo tanto, tenemos

\[\begin{align*}\int \frac{x^2+2x+3}{\sqrt{x}}\ dx &= \int (x^2+2x+3)\cdot2\ du\\ &= \int 2(u^4 + 2u^2 + 3)\ du \\ &= \frac25u^5 + \frac43u^3 + 6u + C \\&= \frac25x^\frac52 + \frac43x^\frac32 + 6x^\frac12+C,\end{align*}\]

que obviamente es la misma respuesta que obtuvimos antes. En esta situación, la sustitución es posiblemente más trabajo que nuestro otro método. Lo fantástico es que funciona. Demuestra lo flexible que es la integración.

Sustitución y funciones trigonométricas inversas

Al estudiar derivadas de funciones inversas, aprendimos que

\[\frac{d}{dx}\big(\tan^{-1}x\big) = \frac{1}{1+x^2}.\]

Aplicar la regla de la cadena a esto no es difícil; por ejemplo,

\[\frac{d}{dx}\big(\tan^{-1}5x\big) = \frac{5}{1+25x^2}.\]

Ahora exploramos cómo la Sustitución puede ser utilizada para “deshacer” ciertas derivadas que son el resultado de la Regla de Cadena aplicada a las funciones trigonométricas inversas. Comenzamos con un ejemplo.

Ejemplo\(\PageIndex{12}\): Integrating by substitution: inverse trigonometric functions

Evaluar\( \int \frac{1}{25+x^2}\ dx\).

Solución

El integrando se parece a la derivada de la función arcotangente. Nota:

\ [\ begin {align}\ frac {1} {25+x^2} &=\ frac {1} {25 (1+\ frac {x^2} {25})}\\ &=\ frac {1} {25 (1+\ izquierda (\ frac {x} {5}\ derecha) ^2)}\\
&=\ frac {1} {25}\ frac {1} {1+\ izquierda (\ frac {x} {5}\ derecha) ^2}\. \ end {align}\]

Así

\[\int\frac{1}{25+x^2}\ dx = \frac{1}{25}\int \frac{1}{1+\left(\frac{x}{5}\right)^2}\ dx.\]

Esto se puede integrar usando Sustitución. Establecer\(u = x/5\), por lo tanto\(du = dx/5\) o\(dx=5du\). Así

\[\begin{align}\int\frac{1}{25+x^2}\ dx &= \frac{1}{25}\int \frac{1}{1+\left(\frac{x}{5}\right)^2}\ dx \\ &= \frac15\int \frac{1}{1+u^2}\ du \\ &= \frac15\tan^{-1}u + C \\ &= \frac15\tan^{-1}\left(\frac x5\right)+C\end{align}\]

Ejemplo\(\PageIndex{12}\) demuestra una técnica general que se puede aplicar a otros integrands que dan como resultado funciones trigonométricas inversas. Los resultados se resumen aquí.

Teorema\(\PageIndex{2}\): Integrals Involving Inverse Trigonomentric Functions

Vamos\(a>0\).

1. \(\displaystyle \int \frac{1}{a^2+x^2}\ dx = \frac1a\tan^{-1}\left(\frac{x}{a}\right) + C\)
2. \(\displaystyle \int \frac{1}{\sqrt{a^2-x^2}}\ dx = \sin^{-1}\left(\frac{x}{a}\right)+C\)
3. \(\displaystyle \int \frac{1}{x\sqrt{x^2-a^2}}\ dx = \frac1a\sec^{-1}\left(\frac{|x|}{a}\right)+C\)

Practicemos usando el Teorema\(\PageIndex{2}\).

Ejemplo\(\PageIndex{13}\): Integrating by substitution: inverse trigonometric functions

Evaluar las integrales indefinidas dadas.
$$\ displaystyle\ int\ frac {1} {9+x^2}\ dx,\ quad\ int\ frac {1} {x\ sqrt {x^2-\ frac {1} {100}}}\ dx\ quad\ texto {y}\ quad\ int\ frac {1} {\ sqrt {5-x^2}}\ dx.\]

Solución

Cada uno puede ser respondido usando una aplicación directa del Teorema\(\PageIndex{2}\).

\(\displaystyle \int \frac{1}{9+x^2}\ dx = \frac13\tan^{-1} \frac x3 + C\), como\(a = 3\).

\(\displaystyle \int \frac{1}{x\sqrt{x^2-\frac{1}{100}}}\ dx = 10\sec^{-1}10x + C\), como\(a = \frac1{10}\).

\(\displaystyle \int \frac{1}{\sqrt{5-x^2}} = \sin^{-1}\frac{x}{\sqrt{5}}+C\), como\(a = \sqrt{5}\).

La mayoría de las aplicaciones del Teorema no\(\PageIndex{2}\) son tan sencillas. Los siguientes ejemplos muestran algunas integrales comunes que aún pueden abordarse con este teorema.

Ejemplo\(\PageIndex{14}\): Integrating by substitution: completing the square

Evaluar\(\displaystyle \int\frac{1}{x^2-4x+13}\ dx\).

Solución

Inicialmente, esta integral parece no tener nada en común con las integrales en Teorema\(\PageIndex{2}\). Al carecer de raíz cuadrada, es casi seguro que no está relacionada con el arcoseno o la secante del arco. Está, sin embargo, relacionado con la función arcangente.

Esto lo vemos completando el cuadrado en el denominador. Damos un breve recordatorio del proceso aquí.

Comience con una cuadrática con un coeficiente inicial de 1. Tendrá la forma de\(x^2 + bx + c\). Tomar 1/2 de\(b\), cuadrarlo, y agregar/restarlo de nuevo en la expresión. Es decir,

\[\begin{align} x^2+bx+ c &= \underbrace{x^2 + bx + \frac{b^2}4}_{(x+b/2)^2} - \frac{b^2}4 + c\\&= \left(x+\frac b2\right)^2 + c-\frac{b^2}4\end{align}\]

En nuestro ejemplo, tomamos la mitad\(-4\) y la cuadramos, consiguiendo\(4\). Lo agregamos o restamos en el denominador de la siguiente manera:

\[\begin{align}\frac{1}{x^2-4x+13} &= \frac{1}{\underbrace{x^2-4x+4}_{(x-2)^2}-4+13}\\ &=\frac{1}{(x-2)^2 + 9}\end{align}\]

Ahora podemos integrar esto usando la regla arcangente. Técnicamente, tenemos que sustituir primero por\(u=x-2\), pero podemos emplear Key Idea 10 en su lugar. Así tenemos

\[ \int \frac{1}{x^2-4x+13}\ dx = \int \frac{1}{(x-2)^2+9}\ dx = \frac13\tan^{-1}\frac{x-2}{3}+C.\]

Ejemplo\(\PageIndex{15}\): Integrals requiring multiple methods

Evaluar\(\displaystyle \int \frac{4-x}{\sqrt{16-x^2}}\ dx\).

Solución

Esta integral requiere de dos métodos diferentes para evaluarla. Llegaremos a esos métodos dividiendo la integral:

\[ \int \frac{4-x}{\sqrt{16-x^2}}\ dx = \int \frac{4}{\sqrt{16-x^2}}\ dx - \int \frac{x}{\sqrt{16-x^2}}\ dx.\]

La primera integral se maneja usando una aplicación directa del Teorema\(\PageIndex{2}\); la segunda integral se maneja por sustitución, con\(u = 16-x^2\). Manejamos cada uno por separado.

\(\displaystyle \int \frac{4}{\sqrt{16-x^2}}\ dx = 4\sin^{-1}\frac{x}{4} + C.\)

\(\displaystyle \int\frac{x}{\sqrt{16-x^2}}\ dx\): Establecer\(u = 16-x^2\), así\(du = -2xdx\) y\(xdx = -du/2\). Tenemos

\[\begin{align} \int\frac{x}{\sqrt{16-x^2}}\ dx &= \int\frac{-du/2}{\sqrt{u}}\\ &= -\frac12\int \frac{1}{\sqrt{u}}\ du \\ &= - \sqrt{u} + C\\ &= -\sqrt{16-x^2} + C.\end{align}\]

Combinando estos juntos, tenemos

\[ \int \frac{4-x}{\sqrt{16-x^2}}\ dx = 4\sin^{-1}\frac x4 + \sqrt{16-x^2}+C.\]

Sustitución e Integración Definitiva

Esta sección se ha centrado en evaluar integrales indefinidas a medida que estamos aprendiendo una nueva técnica para encontrar antiderivados. Sin embargo, gran parte del tiempo la integración se utiliza en el contexto de una integral definida. Las integrales definidas que requieren sustitución se pueden calcular utilizando el siguiente flujo de trabajo:

1. Comience con una integral definida\(\displaystyle \int_a^b f(x)\ dx\) que requiera sustitución.
2. Ignorar los límites; usar la sustitución para evaluar\(\displaystyle \int f(x)\ dx\) y encontrar un antiderivado\(F(x)\).
3. Evaluar\(F(x)\) en los límites; es decir, evaluar\(F(x)\Big|_a^b = F(b) - F(a)\).

Este flujo de trabajo funciona bien, pero la sustitución ofrece una alternativa que es poderosa y sorprendente (y un poco de ahorro de tiempo).

En su esencia, (utilizando la notación de la\(\PageIndex{1}\) sustitución del teorema convierte integrales de la forma\(\displaystyle \int F'(g(x))g'(x)\ dx\) en una integral de la forma\(\displaystyle \int F'(u)\ du\) con la sustitución de\(u = g(x)\). El siguiente teorema establece cómo se pueden cambiar los límites de una integral definida a medida que se realiza la sustitución.

Teorema\(\PageIndex{3}\): Substitution with Definite Integrals

Dejar\(F\) y\(g\) ser funciones diferenciables, donde el rango de\(g\) es un intervalo\(I\) que está contenido en el dominio de\(F\). Entonces

\[\int_a^b F'\big(g(x)\big)g'(x)\ dx = \int_{g(a)}^{g(b)} F'(u)\ du.\]

En efecto, el Teorema\(\PageIndex{3}\) establece que una vez que te conviertes a integrar con respecto a\(u\), no necesitas volver a evaluar con respecto a\(x\). Algunos ejemplos ayudarán a uno a entender.

Ejemplo\(\PageIndex{16}\): Definite integrals and substitution: changing the bounds

Evaluar\(\displaystyle \int_0^2 \cos(3x-1)\ dx\) usando Teorema\(\PageIndex{3}\).

Solución

Observando la composición de las funciones, dejar\(u=3x-1\), de ahí que\(du = 3dx. As \(3dx\)\) no aparezca en el integrando, divida esta última ecuación por 3 para obtener\(du/3 = dx\).

Al establecer\(u = 3x-1\), lo estamos afirmando implícitamente\(g(x) = 3x-1\). Teorema\(\PageIndex{3}\) afirma que el nuevo límite inferior es\(g(0) = -1\); el nuevo límite superior es\(g(2) = 5\). Ahora evaluamos la integral definida:

\[\begin{align}\int_1^2 \cos(3x-1) \ dx &= \int_{-1}^5 \cos u \frac{du}{3} \\ &= \frac{1}{3} \sin u\Big|_{-1}^5 \\ &= \frac{1}{3}\big(\sin 5- \sin (-1)\big)\approx -0.039.\end{align}\]

Observe cómo una vez que convertimos la integral a ser en términos de\(u\), nunca volvimos a usar\(x\).

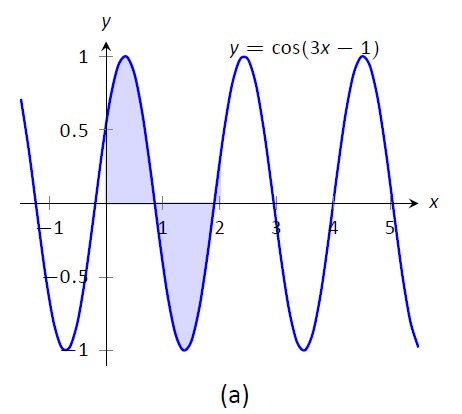
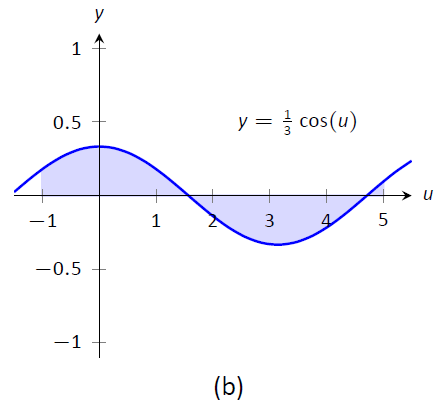
Figura\(\PageIndex{1}\): Graficando las áreas definidas por las integrales definidas de Ejemplo\(\PageIndex{16}\)

Las gráficas en Figura\(\PageIndex{1}\) cuentan más de la historia. En (a) el área definida por el integrando original está sombreada, mientras que en (b) el área definida por el nuevo integrando está sombreada. En esta situación particular, las áreas se ven muy similares; la nueva región es “más corta” pero “más ancha”, dando la misma área.

Ejemplo\(\PageIndex{17}\): Definite integrals and substitution: changing the bounds

Evaluar\(\displaystyle \int_0^{\pi/2} \sin x \cos x\ dx\) usando Teorema\(\PageIndex{3}\).

Solución

Vimos la integral indefinida correspondiente en Ejemplo\(\PageIndex{4}\). En ese ejemplo nos fijamos\(u = \sin x\) pero afirmamos que podríamos haber dejado\(u = \cos x\). Por variedad, hacemos esto último aquí.

Vamos\(u = g(x) = \cos x\), dando\(du = -\sin x\ dx\) y por lo tanto\(\sin x\ dx = -du\). El nuevo límite superior es\(g(\pi/2) = 0\); el nuevo límite inferior es\(g(0) = 1\). Observe cómo el límite inferior es realmente más grande que el límite superior ahora. Tenemos

\[\begin{align} \int_0^{\pi/2} \sin x\cos x\ dx &= \int_1^0 -u\ du \quad \text{\scriptsize (switch bounds \& change sign)}\\ &= \int_0^1 u\ du\\ &= \frac12u^2\Big|_0^1= 1/2.\\ \end{align}\]

En Figura\(\PageIndex{2}\) hemos vuelto a graficar las dos regiones definidas por nuestras integrales definidas. A diferencia del ejemplo anterior, no se parecen entre sí. No obstante, el Teorema\(\PageIndex{3}\) garantiza que tienen la misma área.

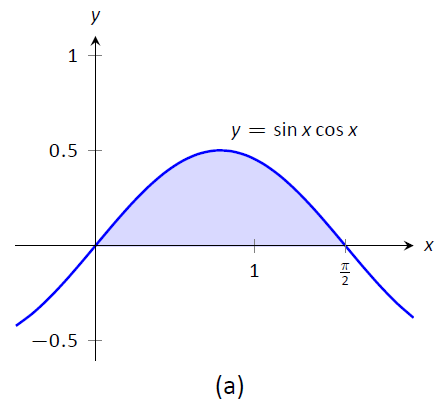
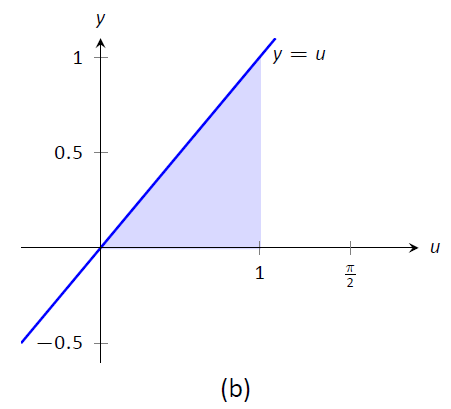
Figura\(\PageIndex{2}\): Graficando las áreas definidas por las integrales definidas de Ejemplo\(\PageIndex{17}\).

La integración por sustitución es una técnica de integración poderosa y útil. En la siguiente sección se introduce otra técnica, llamada Integración por Partes. A medida que la sustitución “deshace” la Regla de Cadena, la integración por partes “deshace” la Regla del Producto. En conjunto, estas dos técnicas proporcionan una base sólida en la que se basan la mayoría de las otras técnicas de integración.

Colaboradores y Atribuciones

• Template:ContribApexCalc
• Template:ContribMarshall