6.2: Integración por Partes

Última actualización
Guardar como PDF

Page ID: 111868

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Aquí hay una integral simple que aún no podemos evaluar:

$$\ int x\ cos x\, dx.\]

Es una cuestión sencilla tomar la derivada del integrando usando la Regla de Producto, pero no existe una Regla de Producto para integrales. Sin embargo, esta sección introduce Integración por Partes, un método de integración que se basa en la Regla de Producto para derivados. Nos permitirá evaluar esta integral.

La Regla del Producto dice que si$u$ y$v$ son funciones de$x$, entonces$(uv)' = u'v + uv'$. Por simplicidad, hemos escrito$u$ para$u(x)$ y$v$ para$v(x)$. Supongamos que integramos ambos lados con respecto a$x$. Esto da

$$\ int (uv) '\, dx =\ int (u'v+uv')\, dx.\]

Por el Teorema Fundamental del Cálculo, el lado izquierdo se integra a$uv$. El lado derecho puede dividirse en dos integrales, y tenemos

$$uv =\ int u'v\, dx +\ int uv'\, dx.\]

Resolviendo para la segunda integral que tenemos

$$\ int uv'\, dx = uv -\ int u'v\, dx.\]

Usando notación diferencial, podemos escribir$du = u'(x)dx$ y$dv=v'(x)dx$ y la expresión anterior se puede escribir de la siguiente manera:

$$\ int u\, dv = uv -\ int v\, du.\]

Esta es la fórmula de Integración por Partes. Para fines de referencia, lo declaramos en un teorema.

Teorema$\PageIndex{1}$: Integration by Parts

Dejar$u$ y$v$ ser funciones diferenciables de$x$ en un intervalo$I$ que contiene$a$ y$b$. Entonces

\[\int u\ dv = uv - \int v\ du,\]

e integración por partes

\[\int_{x=a}^{x=b} u\ dv = uv\Big|_a^b - \int_{x=a}^{x=b}v\ du.\]

Probemos un ejemplo para entender nuestra nueva técnica.

Ejemplo$\PageIndex{1}$: Integrating using Integration by Parts

Evaluar$\displaystyle \int x\cos{x}\ dx$.

Solución

La clave para la Integración por Partes es identificar parte del integrando como "$u$" y parte como "”$dv$.” La práctica regular ayudará a uno a hacer buenas identificaciones, y posteriormente introduciremos algunos principios que ayudan. Por ahora, vamos$u=x$ y$dv=\cos{x}\ dx$.

Generalmente es útil hacer una pequeña tabla de estos valores como se hace a continuación. En este momento solo conocemos$u$ y$dv$ como se muestra a la izquierda de Figura$\PageIndex{1}$; a la derecha rellenamos el resto de lo que necesitamos. Si$u = x$, entonces$du = dx$. Ya que$dv = \cos x\ dx$,$v$ es un antiderivado de$\cos x$. Nosotros elegimos$v = \sin x$.

$alt$

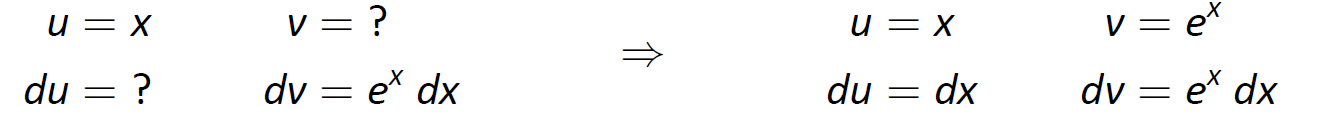
Figura$\PageIndex{1}$: Configuración de la integración por partes.

Ahora sustituya todo esto en la fórmula Integración por Partes, dando

$$\ int x\ cos x\, dx = x\ sin x -\ int\ sin x\, dx.\]

Luego podemos integrarnos$\sin x$ para obtener$-\cos x + C$ y en general nuestra respuesta es

$$\ int x\ cos x\ dx = x\ sin x +\ cos x + C.\]

Observe cómo el antiderivado contiene un producto,$x\sin x$. Este producto es lo que hace que la Integración por Partes sea necesaria.

El ejemplo anterior demuestra cómo funciona la Integración por Partes en general. Intentamos identificar$u$ y$dv$ en la integral nos dan, y la clave es que solemos querer elegir$u$ y$dv$ así eso$du$ es más sencillo que$u$ y$v$ ojalá no sea demasiado más complicado que$dv$. Esto significará que la integral del lado derecho de la fórmula Integración por Partes,$\int v\,du$ será más simple de integrar que la integral original$\int u\,dv$.

En el ejemplo anterior, elegimos$u=x$ y$dv=\cos x\,dx$. Entonces$du=dx$ fue más simple que$u$ y no$v=\sin x$ es más complicado que$dv$. Por lo tanto, en lugar de$x\cos x \,dx$ integrarnos$\sin x\,dx$, podríamos integrar, lo que sabíamos hacer.

Un mnemotécnico útil para ayudar a determinar$u$ es “LIATE”, donde

\[L = \textbf{L}ogarithmic, I = \textbf{I}nverse Trig., A = \textbf{A}lgebraic (polynomials),\]

\[T = \textbf{T}rigonometric, and E = \textbf{E}xponential.\]

Si el integrando contiene tanto un término logarítmico como un término algebraico, en general dejando$u$ ser el término logarítmico funciona mejor, como lo indica L que viene antes de A en LIATE.

Consideramos ahora otro ejemplo.

Ejemplo$\PageIndex{2}$: Integrating using Integration by Parts

Evaluar$\displaystyle \int x e^x\,dx$.

Solución

El integrando contiene un término A lgebraico ($x$) y un término xponencial\ textbf {E} ($e^x$). Nuestra mnemotécnica sugiere dejar$u$ ser el término algebraico, así que elegimos$u=x$ y$dv=e^x\,dx$. Entonces$du=dx$ y$v=e^x$ como lo indican las tablas siguientes.

$alt$

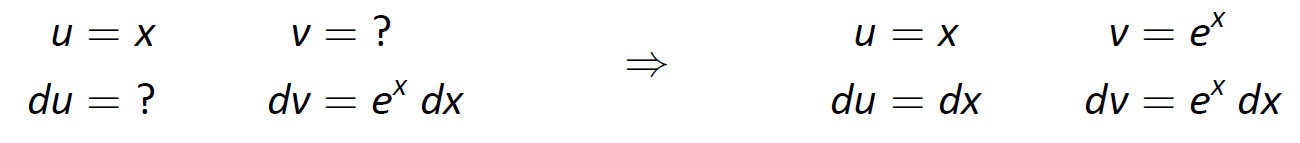
Figura$\PageIndex{2}$: Configuración de la Integración por Partes.

Vemos$du$ es más sencillo que$u$, mientras que no hay cambio en pasar de$dv$ a$v$. Esto es bueno. La fórmula Integración por Partes da

$$\ int x e^x\, dx = xe^x -\ int e^x\, dx.\]

La integral a la derecha es simple; nuestra respuesta final es

$$\ int xe^x\ dx = xe^x - e^x + C.\]

Observe nuevamente cómo los antiderivados contienen un término de producto.

Ejemplo$\PageIndex{3}$: Integrating using Integration by Parts

Evaluar$\displaystyle \int x^2\cos x \,dx$.

Solución

El mnemotécnico sugiere dejar$u=x^2$ en lugar de la función trigonométrica, de ahí$dv=\cos x\,dx$. Entonces$du=2x\,dx$ y$v=\sin x$ como se muestra a continuación.

$alt$

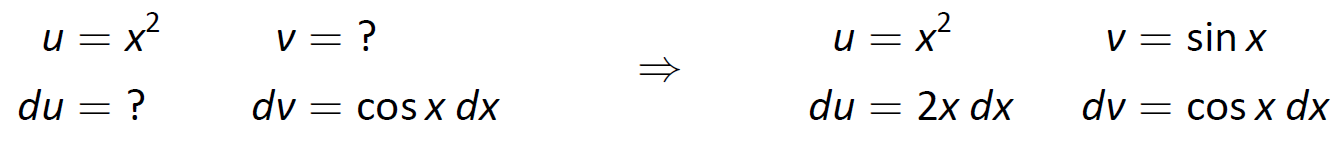
Figura$\PageIndex{3}$: Configuración de la Integración por Partes.

La fórmula Integración por Partes da

$$\ int x^2\ cos x\, dx = x^2\ sin x -\ int 2x\ sin x\, dx.\]

En este punto, la integral de la derecha es efectivamente más simple que la que empezamos con, pero para evaluarla, necesitamos volver a hacer Integración por Partes. Aquí elegimos$u=2x$ y$dv=\sin x$ y rellenamos el resto a continuación.

$alt$

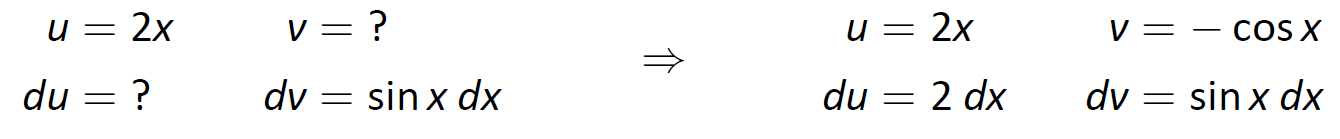
Figura$\PageIndex{4}$: Configuración de la Integración por Partes.

La integral todo el camino a la derecha es ahora algo que podemos evaluar. Evalúa a$-2\sin{x}$. Después pasando y simplificando, teniendo cuidado de mantener todas las señales rectas, nuestra respuesta es
$$\ int x^2\ cos x\ dx = x^2\ sin x + 2x\ cos x - 2\ sin x + C.\]

Ejemplo$\PageIndex{4}$: Integrating using Integration by Parts

Evaluar$\displaystyle \int e^x\cos x \,dx$.

Solución

Este es un problema clásico. Nuestro mnemotécnico sugiere dejar$u$ ser la función trigonométrica en lugar de la exponencial. En este ejemplo particular, uno puede dejar$u$ ser cualquiera$\cos x$ o$e^x$; para demostrar que no tenemos que seguir LIATE, elegimos$u=e^x$ y de ahí$dv = \cos x\,dx$. Entonces$du=e^x\,dx$ y$v=\sin x$ como se muestra a continuación.

$alt$

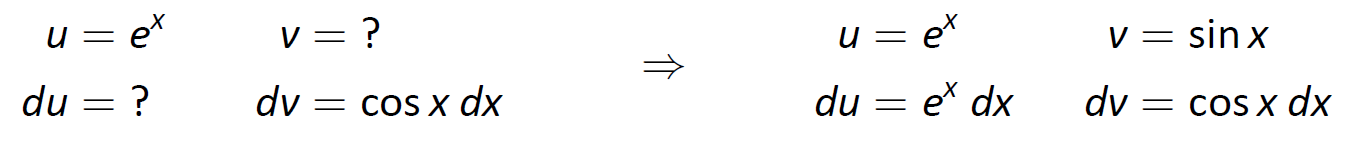
Figura$\PageIndex{5}$: Configuración de la Integración por Partes.

Observe que no$du$ es más sencillo que$u$, ir en contra de nuestra regla general (pero tenga en cuenta con nosotros). La fórmula Integración por Partes rinde

$$\ int e^x\ cos x\ dx = e^x\ sin x -\ int e^x\ sin x\, dx.\]

La integral de la derecha no es muy diferente a la que empezamos con, así que parece que no hemos llegado a ninguna parte. Sigamos trabajando y apliquemos Integración por Partes a la nueva integral, usando$u=e^x$ y$dv = \sin x\,dx$. Esto nos lleva a lo siguiente:

$alt$

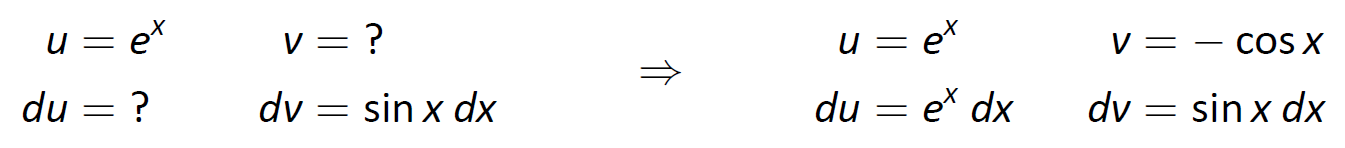
Figura$\PageIndex{6}$: Configuración de la Integración por Partes.

La fórmula Integración por Partes da entonces:

\[\begin{align*} \int e^x\cos x\,dx &= e^x\sin x - \left(-e^x\cos x - \int -e^x\cos x\,dx\right)\\ &= e^x\sin x+ e^x\cos x - \int e^x\cos x\ dx.\end{align*}\]

Parece que estamos de vuelta justo donde empezamos, ya que el lado derecho contiene$\int e^x\cos x\,dx$. Pero esto en realidad es algo bueno.

Añadir$\int e^x\cos x\ dx$ a ambos lados. Esto da

\ [\ begin {align*} 2\ int e^x\ cos x\ dx & = e^x\ sin x + e^x\ cos x\\ text {Ahora divide ambos lados por 2:}
\ int e^x\ cos x\ dx & =\ frac {1} {2}\ grande (e^x\ sin x + e^x\ cos x\ big). \ end {alinear*}\]

Simplificando un poco y sumando la constante de integración, nuestra respuesta es así

$$\ int e^x\ cos x\ dx =\ frac12e^x\ izquierda (\ sin x +\ cos x\ derecha) +C.\]

Ejemplo$\PageIndex{5}$: Integrating using Integration by Parts: antiderivative of $\ln x$

Evaluar$\displaystyle \int \ln x\,dx$.

Solución

Se puede haber notado que tenemos reglas para integrar las funciones trigonométricas familiares y$e^x$, pero aún no hemos dado una regla para la integración$\ln x$. Eso es porque no se$\ln x$ puede integrar fácilmente con ninguna de las reglas que hemos aprendido hasta este punto. Pero podemos encontrar su antiderivado por una aplicación inteligente de Integración por Partes. Establecer$u=\ln x$ y$dv=dx$. Este es un buen truco para aprender, ya que puede ayudar en otras situaciones. Esto determina$du=(1/x)\,dx$ y$v=x$ como se muestra a continuación.

$alt$

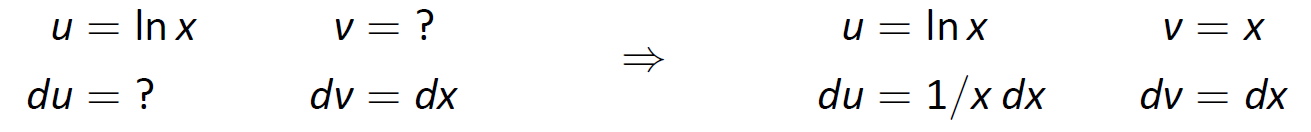
Figura$\PageIndex{7}$: Configuración de la Integración por Partes.

Al juntar todo esto en la fórmula de Integración por Partes, las cosas salen muy bien:

$$\ int\ ln x\, dx = x\ ln x -\ int x\,\ frac1x\, dx.\]

La nueva integral se simplifica a$\int 1\,dx$, que es casi tan simple como se ponen las cosas. Su integral es$x+C$ y nuestra respuesta es

$$\ int\ ln x\ dx = x\ ln {x} - x + C.\]

Ejemplo$\PageIndex{6}$: Integrating using Int. by Parts: antiderivative of $\arctan x$

Evaluar$\displaystyle \int \arctan x \,dx$.

Solución

El mismo truco furtivo que usamos arriba funciona aquí. Dejar$u=\arctan x$ y$dv=dx$. Entonces$du=1/(1+x^2)\,dx$ y$v=x$. La fórmula Integración por Partes da

\[\int \arctan x \,dx = x\arctan x - \int \frac x{1+x^2}\,dx.\]

La integral de la derecha puede resolverse por sustitución. Tomando$u=1+x^2$, obtenemos$du=2x\,dx$. La integral se convierte entonces

\[\int \arctan x \,dx = x\arctan x - \frac12\int \frac 1{u}\,du.\]

La integral de la derecha evalúa a$\ln|u|+C$, que se convierte$\ln(1+x^2)+C$. Por lo tanto, la respuesta es

\[\int \arctan x\ dx = x\arctan x - \ln(1+x^2) + C.\]

Sustitución antes de la integración

Al tomar derivados, era común emplear múltiples reglas (como usar tanto el Cociente como las Reglas de Cadena). Entonces no debería sorprender que algunas integrales se evalúen mejor combinando técnicas de integración. En particular, aquí ilustramos haciendo una sustitución “inusual” primero antes de usar Integration by Parts.

Ejemplo$\PageIndex{7}$: Integration by Parts after substitution

Evaluar$\displaystyle \int \cos(\ln x)\ dx$.

Solución

El integrando contiene una composición de funciones, llevándonos a pensar que la sustitución sería beneficiosa. Dejando$u=\ln x$, tenemos$du = 1/x\ dx$. Esto parece problemático, ya que no tenemos un$1/x$ en el integrando. Pero considere:

\[du = \frac 1x\ dx \Rightarrow x\cdot du = dx.\]

Ya que$u = \ln x$, podemos usar funciones inversas y concluir que$x = e^u$. Por lo tanto tenemos que

\[\begin{align*} dx &= x\cdot du \\ &= e^u\ du.\end{align*}\]

Así podemos sustituir$\ln x$ con$u$ y$dx$ con$e^u\ du$. Así reescribimos nuestra integral como

\[\int \cos(\ln x)\ dx = \int e^u\cos u \ du.\]

Evaluamos esta integral en Ejemplo$\PageIndex{4}$. Usando el resultado ahí, tenemos:

\[\begin{align*}\int \cos(\ln x)\ dx &= \int e^u\cos u \ du \\ &= \frac12e^u\big(\sin u + \cos u\big) + C \\&= \frac12e^{\ln x} \big(\sin(\ln x) + \cos (\ln x)\big)+C\\ &= \frac12x \big(\sin(\ln x) + \cos (\ln x)\big)+C.\end{align*}\]

Integrales definidas e integración por partes

Hasta el momento nos hemos centrado únicamente en evaluar integrales indefinidas. Por supuesto, podemos usar Integración por Partes para evaluar integrales definidas también, como$\PageIndex{1}$ estados del Teorema. Lo hacemos en el siguiente ejemplo.

Ejemplo$\PageIndex{8}$: Definite integration using Integration by Parts

Evaluar$\displaystyle \int_1^2 x^2 \ln x \,dx$.

Solución

Nuestro mnemotécnico sugiere dejar$u=\ln x$, por lo tanto$dv =x^2\,dx$.

Luego obtenemos$du = (1/x)\,dx$ y$v=x^3/3$ como se muestra a continuación.

$alt$

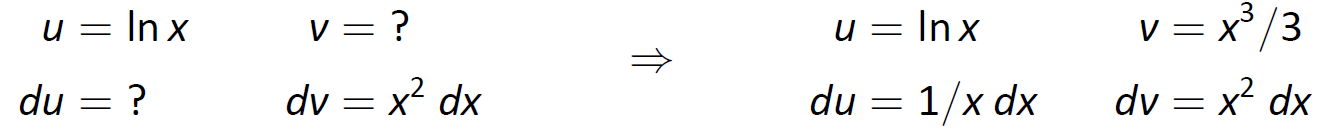
Figura$\PageIndex{8}$: Configuración de la Integración por Partes.

La fórmula Integración por Partes da entonces

\[\begin{align*} \int_1^2 x^2 \ln x\,dx &= \frac{x^3}3\ln x\bigg|_1^2 - \int_1^2 \frac{x^3}{3}\,\frac 1x\,dx \\&= \frac{x^3}3\ln x\bigg|_1^2 - \int_1^2 \frac{x^2}{3}\,dx \\ &= \frac{x^3}3\ln x\bigg|_1^2 - \frac{x^3}{9}\bigg|_1^2\\&= \left(\frac{x^3}3\ln x - \frac{x^3}{9}\right)\bigg|_1^2\\ &= \left(\frac83\ln 2 - \frac89\right)-\left(\frac13\ln 1 - \frac19\right) \\ &= \frac83\ln 2 - \frac79 \\ &\approx 1.07.\end{align*}\]

En general, Integration by Parts es útil para integrar ciertos productos de funciones, como$\int x e^x\,dx$ o$\int x^3\sin x\,dx$. También es útil para integrales que involucran logaritmos y funciones trigonométricas inversas.

Como se indicó anteriormente, la integración es generalmente más difícil que la derivación. Estamos desarrollando herramientas para manejar una gran variedad de integrales, y la experiencia nos dirá cuándo una herramienta es preferible/necesaria sobre otra. Por ejemplo, considere las tres integrales de aspecto similar

$$\ int xe^x\, dx,\ qquad\ int x e^ {x^2}\, dx\ qquad\ texto {y}\ qquad\ int xe^ {x^3}\, dx.\]

Si bien el primero se calcula fácilmente con Integración por Partes, el segundo se aborda mejor con Sustitución. Llevando las cosas un paso más allá, la tercera integral no tiene respuesta en términos de funciones elementales, por lo que ninguno de los métodos que aprendemos en el cálculo nos dará la respuesta exacta.

La integración por Partes es un método muy útil, solo superado por la sustitución. En las siguientes secciones de este capítulo, seguimos aprendiendo otras técnicas de integración. La siguiente sección se centra en el manejo de integrales que contienen funciones trigonométricas.