6.3: Integrales trigonométricas

Última actualización
Guardar como PDF

Page ID: 111911

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Las funciones que involucran funciones trigonométricas son útiles ya que son buenas para describir el comportamiento periódico. En esta sección se describen varias técnicas para encontrar antiderivados de ciertas combinaciones de funciones trigonométricas.

Integrales de la forma$\int \sin^m x\cos^n x\ dx$

Al aprender la técnica de Sustitución, vimos la integral$\int \sin x\cos x\ dx$ en el Ejemplo 6.1.4. La integración no fue difícil, y se podía evaluar fácilmente la integral indefinida dejando$u=\sin x$ o dejando$u = \cos x$. Esta integral es fácil ya que la potencia tanto del seno como del coseno es de 1.

Generalizamos esta integral y consideramos integrales de la forma$\int \sin^mx\cos^nx\ dx$, donde$m,n$ son enteros no negativos. Nuestra estrategia para evaluar estas integrales es utilizar la identidad$\cos^2x+\sin^2x=1$ para convertir altas potencias de una función trigonométrica en la otra, dejando un solo término sinusoidal o coseno en el integrando. Resumimos la técnica general en la siguiente Idea Clave.

Idea Clave 11: Integrales que involucran potencias de seno y coseno

Considere$ \int \sin^mx\cos^nx\ dx$, donde$m,n$ están los enteros no negativos.

Si$m$ es impar, entonces$m=2k+1$ para algún entero$k$. Reescribir $$\ sin^mx =\ sin^ {2k+1} x =\ sin^ {2k} x\ sin x = (\ sin^2x) ^k\ sin x = (1-\ cos^2x) ^k\ sin x.$$ Entonces $$\ int\ sin^mx\ cos^nx\ dx =\ int (1-\ cos^2x) ^k\ sin x\ cos^nx\ dx = -\ int (1-u^2) ^ku^n\ du, $$ donde$u = \cos x$ y$du = -\sin x\ dx$.
Si$n$ es impar, entonces usando sustituciones similares a las descritas anteriormente tenemos $$\ int\ sin^mx\ cos^nx\ dx =\ int u^m (1-u^2) ^k\ du, $$ donde$u = \sin x$ y$du = \cos x\ dx$.
Si ambos$m$ y$n$ son pares, usa el poder—reduciendo identidades $$\ cos^2x =\ frac {1+\ cos (2x)} {2}\ quad\ text {y}\ quad\ sin^2x =\ frac {1-\ cos (2x)} 2$$ para reducir el grado del integrando. Ampliar el resultado y aplicar de nuevo los principios de esta Idea Clave.

Practicamos aplicar la Idea Clave 11 en los siguientes ejemplos.

Ejemplo$\PageIndex{1}$: Integrating powers of sine and cosine

Evaluar$\int\sin^5x\cos^8x\ dx$.

Solución

El poder del término sinusoidal es impar, así que reescribimos$\sin^5x$ como

\[\sin^5x = \sin^4x\sin x = (\sin^2x)^2\sin x = (1-\cos^2x)^2\sin x. \nonumber \]

Nuestra integral es ahora$ \int (1-\cos^2x)^2\cos^8x\sin x\ dx$. Vamos$u = \cos x$, de ahí$du = -\sin x\ dx$. Hacer la sustitución y ampliar el integrando da

\[\int (1-\cos^2)^2\cos^8x\sin x\ dx = -\int (1-u^2)^2u^8\ du = -\int \big(1-2u^2+u^4\big)u^8\ du = -\int \big(u^8-2u^{10}+u^{12}\big)\ du. \nonumber \]

Esta integral final no es difícil de evaluar, dando

\[\begin{align*} -\int \big(u^8-2u^{10}+u^{12}\big)\ du &= -\frac19u^9 + \frac2{11}u^{11} - \frac1{13}u^{13} + C \\[4pt] &=-\frac19\cos^9 x + \frac2{11}\cos^{11} x - \frac1{13}\cos^{13} x + C.\end{align*}\]

Ejemplo$\PageIndex{2}$: Integrating powers of sine and cosine

Evaluar$\int\sin^5x\cos^9x\ dx$.

Solución

Los poderes tanto de los términos seno como de coseno son impares, por lo que podemos aplicar las técnicas de la Idea Clave 11 a cualquiera de las dos potencias. Elegimos trabajar con el poder del término coseno ya que en el ejemplo anterior se utilizó el poder del término sinusoidal.

Reescribimos$\cos^9x$ como

\[\begin{align*} \cos^9 x &= \cos^8x\cos x \\[4pt] &= (\cos^2x)^4\cos x \\[4pt] &= (1-\sin^2x)^4\cos x \\[4pt] &= (1-4\sin^2x+6\sin^4x-4\sin^6x+\sin^8x)\cos x.\end{align*}\]

Reescribimos la integral como

\[\int\sin^5x\cos^9x\ dx = \int\sin^5x\big(1-4\sin^2x+6\sin^4x-4\sin^6x+\sin^8x\big)\cos x\ dx. \nonumber \]

Ahora sustituya e integre, usando$u = \sin x $ y$du = \cos x\ dx$.

\[\begin{align*} \int u^5(1-4u^2+6u^4-4u^6+u^8)\ du &= \int\big(u^5-4u^7+6u^9-4u^{11}+u^{13}\big)\ du \\[4pt]&= \frac16u^6-\frac12u^8+\frac35u^{10}-\frac13u^{12}+\frac{1}{14}u^{14}+C\\[4pt] &= \frac16\sin^6 x-\frac12\sin^8 x+\frac35\sin^{10} x+\ldots\\[4pt]&\phantom{=}-\frac13\sin^{12} x+\frac{1}{14}\sin^{14} x+C.\end{align*}\]

Nota tecnológica: El trabajo que estamos haciendo aquí puede ser un poco tedioso, pero las habilidades desarrolladas (resolución de problemas, manipulación algebraica, etc.) son importantes. Hoy en día los problemas de este tipo suelen resolverse utilizando un sistema de álgebra computacional. El poderoso programa Mathematica se integra$\int \sin^5x\cos^9x\ dx$ como

\[f(x)=-\frac{45 \cos (2 x)}{16384}-\frac{5 \cos (4 x)}{8192}+\frac{19 \cos (6x)}{49152}+\frac{\cos (8x)}{4096}-\frac{\cos (10 x)}{81920}-\frac{\cos (12 x)}{24576}-\frac{\cos (14 x)}{114688},\]

que claramente tiene una forma diferente a nuestra respuesta en Ejemplo$\PageIndex{2}$, que es

\[g(x)=\frac16\sin^6 x-\frac12\sin^8 x+\frac35\sin^{10} x-\frac13\sin^{12} x+\frac{1}{14}\sin^{14} x.\]

La figura$\PageIndex{1}$ muestra una gráfica de$f$ y$g$; claramente no son iguales, sino que difieren solo por una constante. Eso es$g(x) = f(x) + C$ para alguna constante$C$. Entonces tenemos dos antiderivadas diferentes de una misma función, lo que significa que ambas respuestas son correctas.

$alt$

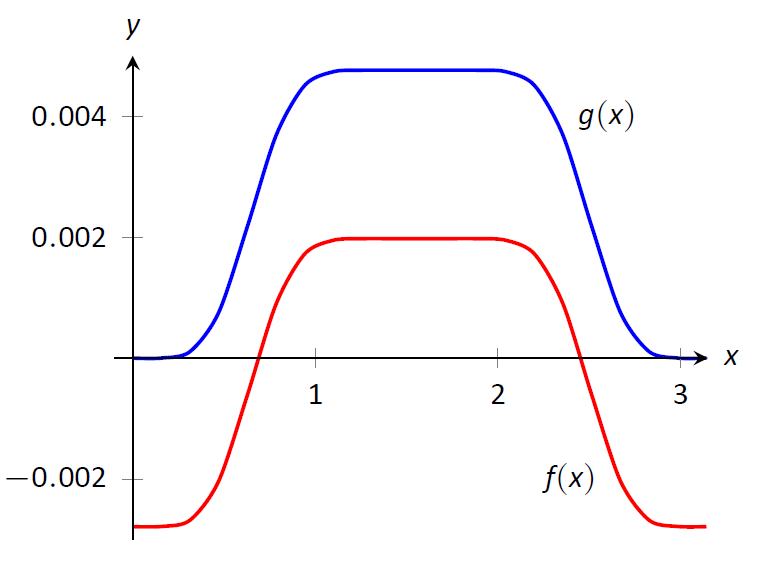
Figura$\PageIndex{1}$: Una gráfica de$f(x)$ y$g(x)$ de Ejemplo$\PageIndex{2}$ y la Nota Tecnológica.

Ejemplo$\PageIndex{3}$: Integrating powers of sine and cosine

Evaluar$\int\cos^4x\sin^2x\ dx$.

Solución

Los poderes de seno y coseno son ambos pares, por lo que empleamos las fórmulas reductoras de poder y el álgebra de la siguiente manera.

\[\begin{align*}\int \cos^4x\sin^2x\ dx &= \int\left(\frac{1+\cos(2x)}{2}\right)^2\left(\frac{1-\cos(2x)}2\right)\ dx \\[4pt] &= \int\frac{1+2\cos(2x)+\cos^2(2x)}4\cdot\frac{1-\cos(2x)}2\ dx\\[4pt] &= \int \frac18\big(1+\cos(2x)-\cos^2(2x)-\cos^3(2x)\big)\ dx\end{align*}\]

El$\cos(2x)$ término es fácil de integrar, especialmente con Key Idea 10. El$\cos^2(2x)$ término es otra integral trigonométrica con una potencia uniforme, requiriendo nuevamente la fórmula reductora de potencia. El$\cos^3(2x)$ término es una función coseno con una potencia impar, requiriendo una sustitución como se hizo antes. Integramos cada uno a su vez a continuación.

\[\int\cos(2x)\ dx = \frac12\sin(2x)+C.\nonumber \]

\[\int\cos^2(2x)\ dx = \int \frac{1+\cos(4x)}2\ dx = \frac12\big(x+\frac14\sin(4x)\big)+C. \nonumber \]

Finalmente, reescribimos$\cos^3(2x)$ como

\[\cos^3(2x) = \cos^2(2x)\cos(2x) = \big(1-\sin^2(2x)\big)\cos(2x).\]

Dejando$u=\sin(2x)$, tenemos$du = 2\cos(2x)\ dx$, por lo tanto

\[\begin{align*} \int \cos^3(2x)\ dx &= \int\big(1-\sin^2(2x)\big)\cos(2x)\ dx\\[4pt] &= \int \frac12(1-u^2)\ du\\[4pt] &= \frac12\Big(u-\frac13u^3\Big)+C\\[4pt] &= \frac12\Big(\sin(2x)-\frac13\sin^3(2x)\Big)+C\end{align*}\]

Juntando todas las piezas, tenemos

\[\begin{align*}\int \cos^4x\sin^2x\ dx &=\int \frac18\big(1+\cos(2x)-\cos^2(2x)-\cos^3(2x)\big)\ dx \\[4pt] &= \frac18\Big[x+\frac12\sin(2x)-\frac12\big(x+\frac14\sin(4x)\big)-\frac12\Big(\sin(2x)-\frac13\sin^3(2x)\Big)\Big]+C \\[4pt] &=\frac18\Big[\frac12x-\frac18\sin(4x)+\frac16\sin^3(2x)\Big]+C\end{align*}\]

El proceso anterior fue un poco largo y tedioso, pero es importante poder trabajar un problema como este de principio a fin.

Integrales de la forma$\int\sin(mx)\sin(nx)\ dx,$$\int \cos(mx)\cos(nx)\ dx$, y$\int \sin(mx)\cos(nx)\ dx$.

Las funciones que contienen productos de senos y cosenos de diferentes períodos son importantes en muchas aplicaciones, incluido el análisis de ondas sonoras. Integrales de la forma

\[\int\sin(mx)\sin(nx)\ dx,\quad \int \cos(mx)\cos(nx)\ dx \quad \text{and}\quad\int \sin(mx)\cos(nx)\ dx\]

se abordan mejor aplicando primero las fórmulas Product to Sum que se encuentran en la contraportada de este texto, a saber

\[\begin{align*} \sin(mx)\sin(nx) &= \frac12\Big[\cos\big((m-n)x\big)-\cos\big((m+n)x\big)\Big] \\[4pt]\cos(mx)\cos(nx) &= \frac12\Big[\cos\big((m-n)x\big)+\cos\big((m+n)x\big)\Big] \\[4pt]\sin(mx)\cos(nx) &= \frac12\Big[\sin\big((m-n)x\big)+\sin\big((m+n)x\big)\Big]\end{align*}\]

Ejemplo$\PageIndex{4}$: Integrating products of $\sin(mx)$ and $\cos(nx)$

Evaluar$\int\sin(5x)\cos(2x)\ dx$.

Solución

La aplicación de la fórmula y la posterior integración son sencillas:

\[\begin{align*}\int\sin(5x)\cos(2x)\ dx &= \int \frac12\Big[\sin(3x)+\sin(7x)\Big]\ dx \\[4pt] &= -\frac16\cos(3x) - \frac1{14}\cos(7x) + C\end{align*}\]

Integrales de la forma$\int\tan^mx\sec^nx\ dx$.

Al evaluar integrales de la forma$\int \sin^mx\cos^nx\ dx$, el Teorema de Pitágoras nos permitió convertir incluso las potencias del seno en potencias pares del coseno, y viceversa. Si, por ejemplo, el poder del seno era impar, sacamos uno$\sin x$ y convertimos el poder par restante de$\sin x$ en una función usando potencias de$\cos x$, conduciendo a una fácil sustitución.

La misma estrategia básica se aplica a las integrales de la forma$\int \tan^mx\sec^n x\ dx$, aunque un poco más matizadas. Los siguientes tres hechos resultarán útiles:

$\frac{d}{dx}(\tan x) = \sec^2x$,
$\frac{d}{dx}(\sec x) = \sec x\tan x$, y
$1+\tan^2x = \sec^2x$(el Teorema de Pitágoras).

Si el integrando puede ser manipulado para separar un$\sec^2x$ término con el poder secante restante incluso, o si un$\sec x\tan x$ término puede separarse con el$\tan x$ poder restante incluso, se puede emplear el Teorema de Pitágoras, conduciendo a una simple sustitución. Esta estrategia se esboza en la siguiente Idea Clave.

Idea Clave 12: Integrales que involucran poderes de tangente y secante

Considere$\int\tan^mx\sec^nx\ dx$, donde$m,n$ están los enteros no negativos.

Si$n$ es par, entonces$n=2k$ para algún entero$k$. Reescribe$\sec^nx$ como $$\ seg^nx =\ seg^ {2k} x =\ seg^ {2k-2} x\ seg^2x = (1+\ tan^2x) ^ {k-1}\ seg^2x.$$ Entonces $$\ int\ tan^mx\ seg^nx\ dx=\ int\ tan^mx (1+\ tan^2x) ^ {k-1}\ seg^2x\ dx =\ int ^m (1+u^2) ^ {k-1}\ du, $$ donde$u = \tan x$ y$du = \sec^2x\ dx$.
Si$m$ es impar, entonces$m=2k+1$ para algún entero$k$. Reescribir$\tan^mx\sec^nx$ como $$\ tan^mx\ seg^nx =\ tan^ {2k+1} x\ seg^nx =\ tan^ {2k} x\ seg^ {n-1} x\ seg x\ tan x = (\ seg^2x-1) ^k\ seg^ {n-1} x\ seg x\ tan x.$$ Luego $$\ int\ tan^mx\ seg^nx\ dx=\ int (\ seg^2x-1) ^k\ seg^ {n-1} x\ seg x\ tan x\ dx =\ int (u^2-1) ^ku^ {n-1}\ du, $$ donde$u = \sec x$ y$du = \sec x\tan x\ dx$.
Si$n$ es impar y$m$ es par, entonces$m=2k$ para algún entero$k$. Convertir$\tan^mx $ a$(\sec^2x-1)^k$. Amplíe el nuevo integrando y utilice Integración Por Partes, con$dv = \sec^2x\ dx$.
Si$m$ es par y$n=0$, reescribe$\tan^mx$ como $$\ tan^mx =\ tan^ {m-2} x\ tan^2x =\ tan^ {m-2} x (\ seg^2x-1) =\ tan^ {m-2}\ seg^2x-\ tan^ {m-2} x.$$ Así que $$\ int\ tan^mx\ dx =\ underbrackets {\ int\ tan^ {m-2}\ seg^2x\ dx} _ {\ texto {\ small aplicar regla\ #1}}\ quad -\ underbrackets {\ int\ tan^ {m-2} x\ dx} _ {\ text {\ small aplicar regla\ # 4 otra vez}} . $$

Las técnicas descritas en los ítems 1 y 2 de la Idea Clave 12 son relativamente sencillas, pero las técnicas en los ítems 3 y 4 pueden ser bastante tediosas. Algunos ejemplos ayudarán con estos métodos.

Ejemplo$\PageIndex{5}$: Integrating powers of tangent and secant

Evaluar$\int \tan^2x\sec^6x\ dx$.

Solución

Como el poder de la secante es parejo, usamos la regla #1 de Key Idea 12 y sacamos una$\sec^2x$ en el integrando. Convertimos los poderes restantes de secante en poderes de tangente.

\[\begin{align*}\int \tan^2x\sec^6x\ dx &= \int\tan^2x\sec^4x\sec^2x\ dx \\[4pt] &= \int \tan^2x\big(1+\tan^2x\big)^2\sec^2x\ dx \end{align*}\]

Ahora sustituya, con$u=\tan x$, con$du = \sec^2x\ dx$.

\[=\int u^2\big(1+u^2\big)^2\ du \nonumber \]

Dejamos la integración y posterior sustitución al lector. La respuesta final es

\[=\frac13\tan^3x+\frac25\tan^5x+\frac17\tan^7x+C. \nonumber \]

Ejemplo$\PageIndex{6}$: Integrating powers of tangent and secant

Evaluar$\int \sec^3x\ dx$.

Solución

Aplicamos la regla #3 de la Idea Clave 12 ya que el poder de secante es impar y el poder de tangente es par (0 es un número par). Utilizamos Integración por Partes; la regla sugiere dejar$dv = \sec^2x\ dx$, lo que significa que$u = \sec x$.

\[\begin{align*}u&= \sec x & v&=\text{?}\\[4pt]du&= \text{?} & dv&=\sec^2 x\ dx\end{align*}\]

Figura$\PageIndex{2}$: Configuración de la Integración por Partes.

Empleando Integración por Partes, tenemos

\[\begin{align*}\int \sec^3x\ dx &= \int \underbrace{\sec x}_u\cdot\underbrace{\sec^2 x\ dx}_{dv}\\[4pt] &= \sec x\tan x - \int \sec x\tan^2x\ dx. \end{align*}\]

Esta nueva integral también requiere aplicar la regla\ #3 de Idea Clave:

\[\begin{align*} &= \sec x\tan x - \int \sec x \big(\sec^2 x-1\big)\ dx\\[4pt] &= \sec x\tan x - \int \sec^3x\ dx + \int \sec x\ dx \\[4pt] &= \sec x\tan x -\int \sec^3x\ dx + \ln|\sec x+\tan x| \\[4pt] \end{align*}\]

En anteriores aplicaciones de Integración por Partes, hemos visto dónde ha reaparecido en nuestro trabajo la integral original. Esto lo resolvemos sumando$\int \sec^3x\ dx$ a ambos lados, dando:

\[\begin{align*} 2\int \sec^3x\ dx &= \sec x\tan x + \ln|\sec x+\tan x| \\[4pt]\int \sec^3x\ dx &= \frac12\Big(\sec x\tan x + \ln|\sec x+\tan x|\Big)+C\end{align*}\]

Damos un ejemplo más.

Ejemplo$\PageIndex{7}$: Integrating powers of tangent and secant

Evaluar$\int\tan^6x\ dx$.

Solución

Empleamos la regla #4 de la Idea Clave 12.

\[\begin{align*} \int \tan^6x\ dx &= \int \tan^4x\tan^2x\ dx \\[4pt] &= \int\tan^4x\big(\sec^2x-1\big)\ dx\\[4pt] &= \int\tan^4x\sec^2x\ dx - \int\tan^4x\ dx \end{align*}\]

Integrar la primera integral con sustitución,$u=\tan x$; integrar la segunda empleando de nuevo la regla #4.

\[\begin{align*} &= \frac15\tan^5x-\int\tan^2x\tan^2x\ dx\\[4pt] &= \frac15\tan^5x-\int\tan^2x\big(\sec^2x-1\big)\ dx \\[4pt]&= \frac15\tan^5x -\int\tan^2x\sec^2x\ dx + \int\tan^2x\ dx\\[4pt] \end{align*}\]

Nuevamente, use la sustitución para la primera integral y la regla\ #4 para la segunda.

\[\begin{align*} &= \frac15\tan^5x-\frac13\tan^3x+\int\big(\sec^2x-1\big)\ dx \\[4pt] &= \frac15\tan^5x-\frac13\tan^3x+\tan x - x+C. \end{align*}\]

Estos últimos ejemplos fueron ciertamente largos, con repetidas aplicaciones de la misma regla. Trate de no sentirse abrumado por la longitud del problema, sino más bien admirar lo robusto que es este método de solución. Una función trigonométrica de alta potencia puede reducirse sistemáticamente a funciones trigonométricas de potencias inferiores hasta que se puedan computar todos los antiderivados.

La siguiente sección introduce una técnica de integración conocida como Sustitución Trigonométrica, una inteligente combinación de Sustitución y el Teorema de Pitágoras.