6.7: Regla de L'Hopital

Si bien este capítulo está dedicado al aprendizaje de técnicas de integración, esta sección no trata sobre la integración. Más bien, se refiere a una técnica de evaluación de ciertos límites que será útil en el siguiente apartado, donde una vez más se discute la integración.

Nuestro tratamiento de los límites nos expuso a “0/0", una forma indeterminada. Si\( \lim_{x\to c}f(x)=0\) y\( \lim_{x\to c} g(x) =0\), no concluimos que\( \lim_{x\to c} f(x)/g(x)\) es\(0/0\); más bien, usamos\(0/0\) como notación para describir el hecho de que tanto el numerador como el denominador se acercan a 0. La expresión 0/0 no tiene valor numérico; se debe realizar otro trabajo para evaluar el límite.

Existen otras formas indeterminadas; son:\(\infty/\infty\),\(0\cdot\infty\),\(\infty-\infty\)\(0^0\),\(1^\infty\) y\(\infty^0\). Así como “0/0" no significa “dividir 0 por 0”, la expresión "\(\infty/\infty\)" no significa “dividir el infinito por el infinito”. En cambio, significa “una cantidad está creciendo sin encuadernación y está siendo dividida por otra cantidad que está creciendo sin ataduras”. No podemos determinar a partir de tal enunciado qué valor, en su caso, resulta en el límite. De igual manera,\(0\cdot \infty\) "" no significa “multiplicar cero por infinito”. En cambio, significa “una cantidad se está reduciendo a cero, y se está multiplicando por una cantidad que está creciendo sin ataduras”. No podemos determinar a partir de tal descripción cuál será el resultado de tal límite.

Esta sección introduce la Regla de L'Hôpital, un método de resolución de límites que producen las formas indeterminadas 0/0 y\(\infty/\infty\). También mostraremos cómo se puede usar la manipulación algebraica para convertir otras expresiones indeterminadas en una de estas dos formas para que se pueda aplicar nuestra nueva regla.

Teorema\(\PageIndex{1}\): L'Hôpital's Rule

Let\(\lim_{x\to c}f(x) = 0\) y\(\lim_{x\to c}g(x)=0\), donde\(f\) y\(g\) son funciones diferenciables en un intervalo abierto\(I\) que contiene\(c\), y\(g'(x)\neq 0\) on\(I\) excepto posiblemente en\(c\). Entonces

$$\ lim_ {x\ a c}\ frac {f (x)} {g (x)} =\ lim_ {x\ a c}\ frac {f' (x)} {g' (x)}.\]

Demostramos el uso de la Regla de L'Hôpital en los siguientes ejemplos; a menudo usaremos “LHR” como abreviatura de “L'Hôpital”

Ejemplo\(\PageIndex{1}\): Using L'Hôpital's Rule

Evaluar los siguientes límites, utilizando la Regla de L'Hôpital según sea necesario.

1. \( \lim_{x\to0}\frac{\sin x}x\)
2. \( \lim_{x\to 1}\frac{\sqrt{x+3}-2}{1-x}\)
3. \( \lim_{x\to0}\frac{x^2}{1-\cos x}\)
4. \( \lim_{x\to 2}\frac{x^2+x-6}{x^2-3x+2}\)

Solución

1. Demostramos que este límite es 1 en Ejemplo\ ref {ex_limit_sinx_prove} usando el Teorema de Squeeze. Aquí utilizamos la Regla de L'Hôpital para mostrar su poder. $$\ lim_ {x\ to0}\ frac {\ sin x} x\ stackrel {\ text {por LHR}\} {=}\ lim_ {x\ to0}\ frac {\ cos x} {1} =1. $$
2. \( \lim_{x\to 1}\frac{\sqrt{x+3}-2}{1-x} \stackrel{\ \text{ by LHR } \ }{=} \lim_{x \to 1} \frac{\frac12(x+3)^{-1/2}}{-1} =-\frac 14.\)
3. \( \lim_{x\to 0}\frac{x^2}{1-\cos x} \stackrel{ \text{ by LHR } }{=} \lim_{x\to 0} \frac{2x}{\sin x}.\)
   Este último límite también evalúa a la forma 0/0 indeterminada. Para evaluarlo, aplicamos de nuevo la Regla de L'Hôpital.$$\ lim_ {x\ a 0}\ frac {2x} {\ sin x}\ stackrel {\ text {por LHR}} {=}\ frac {2} {\ cos x} = 2 .$$ Así\( \lim_{x\to0}\frac{x^2}{1-\cos x}=2.\)
4. Ya sabemos evaluar este límite; primero factorizar el numerador y denominador. Entonces tenemos: $$\ lim_ {x\ a 2}\ frac {x^2+x-6} {x^2-3x+2} =\ lim_ {x\ a 2}\ frac {(x-2) (x+3)} {(x-2) (x-1)} =\ lim_ {x\ a 2}\ frac {x+3} {x-1} = 5.$$ Ahora mostramos como resolver esto usando la Regla de L'Hôpital. $$\ lim_ {x\ a 2}\ frac {x^2+x-6} {x^2-3x+2}\ stackrel {\ text {por LHR}} {=}\ lim_ {x\ a 2}\ frac {2x+1} {2x-3} = 5. $$

Obsérvese que en cada paso donde se aplicaba la Regla de L'Hôpital, se necesitaba: el límite inicial devolvía la forma indeterminada de "”\(0/0\). Si el límite inicial devuelve, por ejemplo, 1/2, entonces no se aplica la Regla de L'Hôpital.

El siguiente teorema extiende nuestra versión inicial de la Regla de L'Hôpital de dos maneras. Permite aplicar la técnica a la forma indeterminada\(\infty/\infty\) y a los límites donde se\(x\) aproxima\(\pm\infty\).

Teorema\(\PageIndex{2}\): L'Hôpital's Rule, Part 2

1. Let\(\lim_{x\to a}f(x) = \pm\infty\) y\(\lim_{x\to a}g(x)=\pm \infty\), donde\(f\) y\(g\) son diferenciables en un intervalo abierto\(I\) que contiene\(a\). Entonces $$\ lim_ {x\ a}\ frac {f (x)} {g (x)} =\ lim_ {x\ a}\ frac {f' (x)} {g' (x)} . $$
2. Dejar\(f\) y\(g\) ser funciones diferenciables en el intervalo abierto\((a,\infty)\) para algún valor\(a\), donde\(g'(x)\neq 0\) on\((a,\infty)\) y\(\lim_{x\to\infty} f(x)/g(x)\) devuelve 0/0 o\(\infty/\infty\). Entonces $$\ lim_ {x\ to\ infty}\ frac {f (x)} {g (x)} =\ lim_ {x\ to\ infty}\ frac {f' (x)} {g' (x)} .$$ Se puede hacer una declaración similar para los límites donde se\(x\) aproxima\(-\infty\).

Ejemplo\(\PageIndex{2}\): L'Hôpital's Rule with limits involving \(\infty\)

Evaluar los siguientes límites.

$$ 1.\\ lim_ {x\ a\ infty}\ frac {3x^2-100x+2} {4x^2+5x-1000}\ qquad\ qquad 2.\\ lim_ {x\ a\ infty}\ frac {e^x} {x^3}.\]

Solución

1. Podemos evaluar este límite ya usando Teorema\ ref {thm:lim_rational_fn_at_infty}; la respuesta es 3/4. Aplicamos la Regla de L'Hôpital para demostrar su aplicabilidad. $$\ lim_ {x\ a\ infty}\ frac {3x^2-100x+2} {4x^2+5x-1000}\ stackrel {\\ text {por LHR}\} {=}\ lim_ {x\ a\ infty}\ frac {6x-100} {8x+5}\ stackrel {\\ text {por LHR}\} {=}\ lim_ {x\ a\ infty}\ frac68 =\ frac34. $$
2. $$\ lim_ {x\ a\ infty}\ frac {e^x} {x^3}\ stackrel {\\ text {por LHR}\} {=}\ lim_ {x\ a\ infty}\ frac {e^x} {3x^2}\ stackrel {\\ text {por LHR}\} {=}\ lim_ {x\ a\ infty}\ frac {e^x} {6x}\ stackrel {\\ text {por LHR}\} {=}\ lim_ {x\ a\ infty}\ frac {e^x} {6} =\ infty.$$ Recordemos que esto significa que el límite no existe; como \(x\)enfoques\(\infty\), la expresión\(e^x/x^3\) crece sin ataduras. Podemos inferir de esto que\(e^x\) crece “más rápido” que\(x^3\); a medida que\(x\) se hace grande,\(e^x\) es mucho más grande que\(x^3\). (Esto tiene implicaciones importantes en la computación al considerar la eficiencia de los algoritmos).

La Regla de L'Hôpital sólo se puede aplicar a las proporciones de funciones. Ante una forma indeterminada como\(0\cdot\infty\) o\(\infty-\infty\), a veces podemos aplicar álgebra para reescribir el límite para que se pueda aplicar la Regla de L'Hôpital. Demostramos la idea general en el siguiente ejemplo.

Ejemplo\(\PageIndex{3}\): Applying L'Hôpital's Rule to other indeterminate forms

Evaluar los siguientes límites.

1. \( \lim_{x\to0^+} x\cdot e^{1/x}\)
2. \( \lim_{x\to0^-} x\cdot e^{1/x}\)
3. \( \lim_{x\to\infty} \ln(x+1)-\ln x\)
4. \( \lim_{x\to\infty} x^2-e^x\)

Solución

1. Como\(x\rightarrow 0^+\),\(x\rightarrow 0\) y\(e^{1/x}\rightarrow \infty\). Así tenemos la forma indeterminada\(0\cdot\infty\). Reescribimos la expresión\(x\cdot e^{1/x}\) como\(\frac{e^{1/x}}{1/x}\); ahora, as\(x\rightarrow 0^+\), obtenemos la forma indeterminada\(\infty/\infty\) a la que se puede aplicar la Regla de L'Hôpital. $$\ lim_ {x\ to0^+} x\ cdot e^ {1/x} =\ lim_ {x\ a 0^+}\ frac {e^ {1/x}} {1/x}\ stackrel {\\ text {por LHR}\} {=}\ lim_ {x\ a 0^+}\ frac {(-1/x^2) e^ {1/x}} {-1/x^2} =\ lim_ {x\ a 0^+} e^ {1/x} =\ infty.$$ Interpretación:\(e^{1/x}\) crece “más rápido” que\(x\) se encoge a cero, es decir, su producto crece sin atarse.
2. Como\(x\rightarrow 0^-\),\(x\rightarrow 0\) y\(e^{1/x}\rightarrow e^{-\infty}\rightarrow 0\). El límite se evalúa a\(0\cdot 0\) lo que no es una forma indeterminada. Concluimos entonces que $$\ lim_ {x\ a 0^-} x\ cdot e^ {1/x} = 0.\]
3. Este límite inicialmente se evalúa a la forma indeterminada\(\infty-\infty\). Al aplicar una regla logarítmica, podemos reescribir el límite como
   $$\ lim_ {x\ a\ infty}\ ln (x+1) -\ ln x =\ lim_ {x\ a\ infty}\ ln\ left (\ frac {x+1} x\ right) .$$ Como\(x\rightarrow \infty\), se acerca el argumento del\(\ln\) término\(\infty/\infty\), a lo que podemos aplicar la Regla de L'Hôpital. $$\ lim_ {x\ a\ infty}\ frac {x+1} x\ stackrel {\\ text {por LHR}\} {=}\ frac11=1.$$ Ya que\(x\rightarrow \infty\) implica\(\frac{x+1}x\rightarrow 1\), se deduce que $$x\ fila derecha\ infty\ quad\ texto {implica}\ quad\ ln\ izquierda (\ frac {x+1} x\ derecha)\ fila derecha\ ln 1=0.\]

   Así $$\ lim_ {x\ a\ infty}\ ln (x+1) -\ ln x =\ lim_ {x\ a\ infty}\ ln\ left (\ frac {x+1} x\ right) =0.$$ Interpretación: ya que este límite evalúa a 0, significa que para grandes\(x\), esencialmente no hay diferencia entre\(\ln (x+1)\) y\(\ln x\); su diferencia es esencialmente 0.

4. El límite devuelve\( \lim_{x\to\infty} x^2-e^x\) inicialmente la forma indeterminada\(\infty-\infty\). Podemos reescribir la expresión factorizando\(x^2\);\( x^2-e^x = x^2\left(1-\frac{e^x}{x^2}\right).\) necesitamos evaluar cómo se\(e^x/x^2\) comporta como\(x\rightarrow \infty\): $$\ lim_ {x\ to\ infty}\ frac {e^x} {x^2}\ stackrel {\\ text {por LHR}\} {=}\ lim_ {x\ to\ infty}\ frac {e^x} {2x}\ stackrel {\\ text {por LHR}\} {=}\ lim_ {x\ a\ infty}\ frac {e^x} {2} =\ infty.\]

   Así\(\lim_{x\to\infty}x^2(1-e^x/x^2)\) evalúa a\(\infty\cdot(-\infty)\), que no es una forma indeterminada; más bien,\(\infty\cdot(-\infty)\) evalúa a\(-\infty\). Concluimos que\( \lim_{x\to\infty} x^2-e^x = -\infty.\)

   Interpretación: a medida que\(x\) se hace grande, la diferencia entre\(x^2\) y\(e^x\) crece muy grande.

Formularios indeterminados\(0^0\),\(1^\infty\) y\(\infty^0\)

Cuando se enfrenta a una forma indeterminada que involucra un poder, a menudo ayuda a emplear la función logarítmica natural. La siguiente Idea Clave expresa el concepto, al que le sigue un ejemplo que demuestra su uso.

Idea clave 20: Evaluar límites que involucran formas indeterminadas\(0^0\), \(1^\infty\) and \(\infty^0\)

Si\( \lim_{x\to c} \ln\big(f(x)\big) = L\), entonces\( \lim_{x\to c} f(x) = \lim_{x\to c} e^{\ln(f(x))} = e\,^L.\)

Ejemplo\(\PageIndex{4}\): Using L'Hôpital's Rule with indeterminate forms involving exponents

Evaluar los siguientes límites.

\( 1. \lim_{x\to\infty} \left(1+\frac1x\right)^x \qquad\qquad 2. \lim_{x\to0^+} x^x.\)

Solución

1. Esto equivale a un límite especial dado en el Teorema\ ref {thm:lim_continuous}; estos límites tienen aplicaciones importantes dentro de las matemáticas y las finanzas. Obsérvese que el exponente se acerca\(\infty\) mientras que la base se acerca a 1, conduciendo a la forma indeterminada\(1^\infty\). Vamos\(f(x) = (1+1/x)^x\); el problema pide evaluar\(\lim_{x\to\infty}f(x)\). Primero evaluemos\( \lim_{x\to\infty}\ln\big(f(x)\big)\). \[\begin{align}\lim_{x\to\infty}\ln\big(f(x)\big) & = \lim_{x\to\infty} \ln \left(1+\frac1x\right)^x \\ &= \lim_{x\to\infty} x\ln\left(1+\frac1x\right)\\ &= \lim_{x\to\infty} \frac{\ln\left(1+\frac1x\right)}{1/x}\end{align}\]Esto produce la forma indeterminada 0/0, por lo que aplicamos la Regla de L'Hôpital. \[\begin{align}&= \lim_{x\to\infty} \frac{\frac{1}{1+1/x}\cdot(-1/x^2)}{(-1/x^2)} \\&= \lim_{x\to\infty}\frac{1}{1+1/x}\\ &= 1. \end{align}\]Así\(\lim_{x\to\infty} \ln \big(f(x)\big) = 1.\) Volvemos al límite original y aplicamos Key Idea 20. $$\ lim_ {x\ a\ infty}\ izquierda (1+\ frac1x\ derecha) ^x =\ lim_ {x\ a\ infty} f (x) =\ lim_ {x\ a\ infty} e^ {\ ln (f (x))} = e^1 = e.\]
2. Este límite lleva a la forma indeterminada\(0^0\). Vamos\(f(x) = x^x\) y consideremos primero\(\lim_{x\to0^+} \ln\big(f(x)\big)\). \[\begin{align} \lim_{x\to0^+} \ln\big(f(x)\big) &= \lim_{x\to0^+} \ln\left(x^x\right) \\ &= \lim_{x\to0^+} x\ln x \\ &= \lim_{x\to0^+} \frac{\ln x}{1/x}.\end{align}\]Esto produce la forma indeterminada\(-\infty/\infty\) por lo que aplicamos la Regla de L'Hôpital. \[\begin{align} &= \lim_{x\to0^+} \frac{1/x}{-1/x^2} \\ &= \lim_{x\to0^+} -x \\ &= 0. \end{align}\]Por lo tanto\(\lim_{x\to0^+} \ln\big(f(x)\big) =0\). Volvemos al límite original y aplicamos Key Idea 20. $$\ lim_ {x\ to0^+} x^x =\ lim_ {x\ to0^+} f (x) =\ lim_ {x\ to0^+} e^ {\ ln (f (x))} = e^0 = 1.$$ Este resultado es apoyado por la gráfica de\(f(x)=x^x\) dado en la Figura\(\PageIndex{1}\).

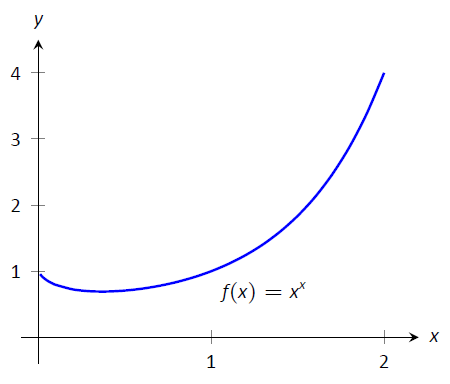
Figura\(\PageIndex{1}\): Una gráfica de\(f(x)=x^x\) sustentar el hecho de que como\(x\to 0^+\),\(f(x)\to 1\).

Nuestra breve revisión de los límites será recompensada en la siguiente sección donde consideremos una integración inadecuada. Hasta el momento, sólo hemos considerado integrales definidas donde los límites son números finitos, como\(\int_0^1 f(x)\ dx\). La integración inadecuada considera integrales donde uno, o ambos, de los límites son “infinitos”. Tales integrales tienen muchos usos y aplicaciones, además de generar ideas que son esclarecedoras.

Colaboradores y Atribuciones

• Template:ContribApexCalc
• Template:ContribMarshall