6.8: Integración inadecuada

Comenzamos esta sección considerando las siguientes integrales definidas:

\[ \int_0^{100}\dfrac1{1+x^2}\ dx \approx 1.5608,\]

\[ \int_0^{1000}\dfrac1{1+x^2}\ dx \approx 1.5698,\]

\[ \int_0^{10,000}\dfrac1{1+x^2}\ dx \approx 1.5707.\]

Observe cómo está el integrando\(1/(1+x^2)\) en cada integral (que se esboza en la Figura\(\PageIndex{1}\)). A medida que el límite superior se hace más grande, uno esperaría que el “área bajo la curva” también crezca. Si bien las integrales definidas sí aumentan de valor a medida que crece el límite superior, no van aumentando mucho. De hecho, considere:

$$\ begin {align}\ int_0^b\ frac {1} {1+x^2}\ dx &=\ left. \ tan^ {-1} x\ derecha|_0^b\\[4pt] &= \tan^{-1}b-\tan^{-1}0 \\[4pt] &= \tan^{-1}b. \end{align}\]

As\(b\rightarrow \infty\),\(\tan^{-1}b \rightarrow \pi/2.\) Por lo tanto parece que a medida que\(b\) crece el límite superior, se\(\int_0^b\frac{1}{1+x^2}\ dx\) acerca el valor de la integral definida\(\pi/2\approx 1.5708\). Esto debería parecerle un poco sorprendente al lector: aunque la curva se extiende “hasta el infinito”, tiene una cantidad finita de área debajo de ella.

Figura\(\PageIndex{1}\): Graficar\( f(x)=\frac{1}{1+x^2}\)

Cuando definimos la integral definida\(\int_a^b f(x)\ dx\), hicimos dos estipulaciones:

1. El intervalo sobre el que nos integramos\([a,b]\),, fue un intervalo finito, y
2. La función\(f(x)\) fue continua\([a,b]\) (asegurando que el rango de\(f\) fue finito).

En esta sección consideramos integrales donde una o ambas de las condiciones anteriores no se mantienen. Tales integrales se llaman integrales inadecuadas.

Integrales inadecuadas con límites infinitos

Definición\(\PageIndex{1}\): Improper Integrals with Infinite Bounds; Converge, Diverge

1. Dejar\(f\) ser una función continua en\([a,\infty)\). Definir $$\ int_a^\ infty f (x)\ dx\ equiv\ lim_ {b\ a\ infty}\ int_a^b f (x)\ dx. $$
2. Dejar\(f\) ser una función continua en\((-\infty,b]\). Define $$\ int_ {-\ infty} ^b f (x)\ dx\ equiv\ lim_ {a\ to-\ infty}\ int_a^b f (x)\ dx. $$
3. Dejar\(f\) ser una función continua en\((-\infty,\infty)\). \(c\)Sea cualquier número real; defina $$\ int_ {-\ infty} ^\ infty f (x)\ dx\ equiv\ lim_ {a\ to-\ infty}\ int_a^c f (x)\ dx\ +\ lim_ {b\ to\ infty}\ int_c^b f (x)\ dx. $$

Se dice que una integral impropia converge si existe su límite correspondiente; de lo contrario, diverge. La integral impropia en la parte 3 converge si y sólo si existen ambos límites.

Ejemplo\(\PageIndex{1}\): Evaluating improper integrals

Evaluar las siguientes integrales inadecuadas.

1. \(\int_1^\infty \frac1{x^2}\ dx\)
2. \(\int_1^\infty \frac1x\ dx\)
3. \(\int_{-\infty}^0 e^x\ dx\)
4. \(\int_{-\infty}^\infty \frac1{1+x^2}\ dx\)

Solución

1. \[\begin{align}[t] \int_1^\infty \frac{1}{x^2}\ dx\ =\ \lim_{b\to\infty} \int_1^b\frac1{x^2}\ dx\ &=\ \lim_{b\to\infty} \frac{-1}{x}\Big|_1^b \\ &= \lim_{b\to\infty} \frac{-1}{b} + 1\\ &= 1.\end{align}\]Una gráfica del área definida por esta integral se da en la Figura\(\PageIndex{2}\).

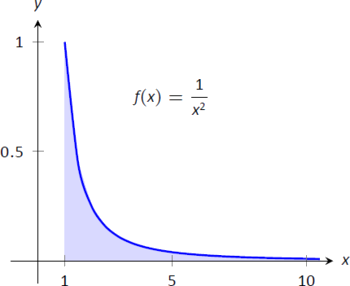
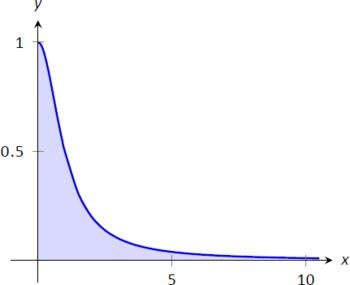
Figura\(\PageIndex{2}\): Una gráfica de\(f(x) = \frac{1}{x^2}\) en Ejemplo\(\PageIndex{1}\).

2. \[\begin{align} \int_1^\infty \frac1x\ dx & = \lim_{b\to\infty}\int_1^b\frac1x\ dx \\ &= \lim_{b\to\infty} \ln |x|\Big|_1^b \\ &= \lim_{b\to\infty} \ln (b)\\ &= \infty. \end{align}\]El límite no existe, de ahí que la integral impropia\(\int_1^\infty\frac1x\ dx\) diverja. Compara las gráficas en figuras\(\PageIndex{3a}\) y\(\PageIndex{3b}\); fíjate como la gráfica de\(f(x) = 1/x\) es notablemente mayor. Esta diferencia es suficiente para hacer que la integral inadecuada diverja.

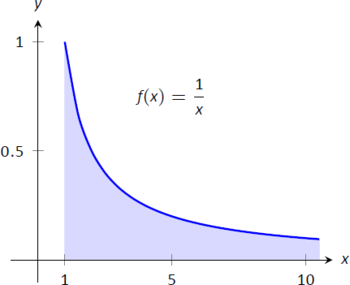
Figura\(\PageIndex{3}\): Un gráfico de\(f(x) = \frac{1}{x}\) en Ejemplo\(\PageIndex{1}\)

3. \[\begin{align} \int_{-\infty}^0 e^x \ dx &= \lim_{a\to-\infty} \int_a^0e^x\ dx \\ &= \lim_{a\to-\infty} e^x\Big|_a^0 \\ &= \lim_{a\to-\infty} e^0-e^a \\&= 1. \end{align}\]Una gráfica del área definida por esta integral se da en la Figura\(\PageIndex{4}\).

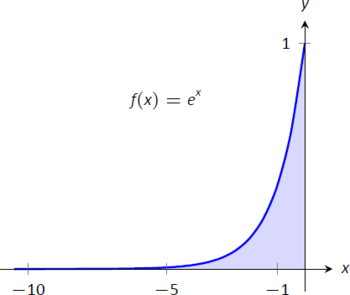
Figura\(\PageIndex{4}\): Un gráfico de\(f(x) = e^x\) en Ejemplo\(\PageIndex{1}\)

4. Tendremos que dividir esto en dos integrales impropias y elegir un valor de\(c\) como en la parte 3 de Definición\(\PageIndex{1}\). Cualquier valor de\(c\) está bien; elegimos\(c=0\). \[\begin{align} \int_{-\infty}^\infty \frac1{1+x^2}\ dx &= \lim_{a\to-\infty} \int_a^0\frac{1}{1+x^2}\ dx + \lim_{b\to\infty} \int_0^b\frac{1}{1+x^2}\ dx \\ &= \lim_{a\to-\infty} \tan^{-1}x\Big|_a^0 + \lim_{b\to\infty} \tan^{-1}x\Big|_0^b\\ &= \lim_{a\to-\infty} \left(\tan^{-1}0-\tan^{-1}a\right) + \lim_{b\to\infty} \left(\tan^{-1}b-\tan^{-1}0\right)\\ &= \left(0-\frac{-\pi}2\right) + \left(\frac{\pi}2-0\right).\end{align}\]Cada límite existe, de ahí que la integral original converja y tenga valor: En la Figura se da\[= \pi.\] una gráfica del área definida por esta integral\(\PageIndex{5}\).

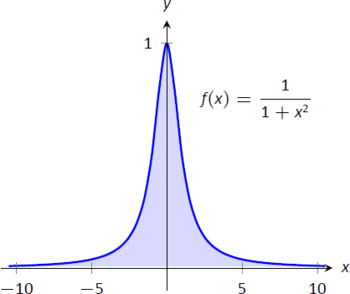
Figura\(\PageIndex{5}\): Un gráfico de\(f(x) = \frac{1}{1+x^2}\) en Ejemplo\(\PageIndex{1}\)

En el apartado anterior se introdujo la Regla de L'Hôpital, un método de evaluación de límites que devuelven formas indeterminadas. No es raro que los límites resultantes de integrales inadecuadas necesiten esta regla como se demuestra a continuación.

Ejemplo\(\PageIndex{2}\): Improper integration and L'Hôpital's Rule

Evaluar la integral inadecuada

\[\int_1^\infty \frac{\ln x}{x^2}\ dx.\]

Solución

Esta integral requerirá el uso de Integración por Partes. Dejar\(u = \ln x\) y\(dv = 1/x^2\ dx\). Entonces

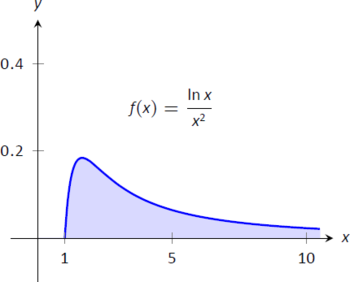
Figura\(\PageIndex{6}\): Un gráfico de\(f(x) = \frac{\ln x}{x^2}\) en Ejemplo\(\PageIndex{2}\)

\[\begin{align}\int_1^\infty\frac{\ln x}{x^2}\ dx &= \lim_{b\to\infty}\int_1^b\frac{\ln x}{x^2}\ dx \\ &= \lim_{b\to\infty}\left(-\frac{\ln x}{x}\Big|_1^b +\int_1^b \frac{1}{x^2} \ dx \right)\\ &= \lim_{b\to\infty} \left.\left(-\frac{\ln x}{x} -\frac1x\right)\right|_1^b\\ &= \lim_{b\to\infty} \left(-\frac{\ln b}{b}-\frac1b - \left(-\ln 1-1\right)\right).\end{align}\]

El\(1/b\) y\(\ln 1\) términos van a 0, dejando\( \lim_{b\to\infty} -\frac{\ln b}b + 1.\) Tenemos que evaluar\( \lim_{b\to\infty} \frac{\ln b}{b}\) con la Regla de L'Hôpital. Contamos con:

\[\begin{align} \lim_{b\to\infty}\frac{\ln b}b &\stackrel{\ \text{ by LHR } \ }{=} \lim_{b\to\infty} \frac{1/b}{1} \\ &= 0.\end{align}\]

Así la integral impropia evalúa como:

\[\int_1^\infty\frac{\ln x}{x^2}\ dx = 1.\]

Integrales inadecuadas con rango infinito

Acabamos de considerar integrales definidas donde el intervalo de integración era infinito. Consideramos ahora otro tipo de integración inadecuada, donde el rango del integrando es infinito.

Definición\(\PageIndex{2}\): Improper Integration with Infinite Range

{Dejar\(f(x)\) ser una función continua en\([a,b]\) excepto en\(c\),\(a\leq c\leq b\), donde\(x=c\) es una asíntota vertical de\(f\). Definir

\[\int_a^b f(x)\ dx = \lim_{t\to c^-}\int_a^t f(x)\ dx + \lim_{t\to c^+}\int_t^b f(x)\ dx.\]

Ejemplo\(\PageIndex{3}\): Improper integration of functions with infinite range

Evalúe las siguientes integrales inadecuadas:

\( 1.\ \int_0^1\frac1{\sqrt{x}}\ dx \hskip 50pt 2. \ \int_{-1}^1\frac{1}{x^2}\ dx.\)

Solución

1. Una gráfica de\(f(x) = 1/\sqrt{x}\) se da en la Figura\(\PageIndex{7}\). Observe que\(f\) tiene una asíntota vertical en\(x=0\); en cierto sentido, estamos tratando de calcular el área de una región que no tiene “top”. ¿Podría esto tener un valor finito? \[\begin{align} \int_0^1 \frac{1}{\sqrt{x}}\ dx &= \lim_{a\to0^+}\int_a^1 \frac1{\sqrt{x}}\ dx \\&=\lim_{a\to0^+} 2\sqrt{x}\Big|_a^1 \\ &= \lim_{a\to0^+} 2\left(\sqrt{1}-\sqrt{a}\right)\\ &= 2.\end{align}\]
   Resulta que la región sí tiene un área finita a pesar de que no tiene límite superior (cosas extrañas pueden ocurrir en matemáticas al considerar el infinito).
   Nota: En Definición\(\PageIndex{1}\),\(c\) puede ser uno de los puntos finales (\(a\)o\(b\)). En ese caso, sólo hay un límite a considerar como parte de la definición.

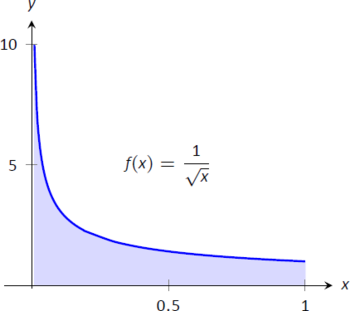
Figura\(\PageIndex{7}\): Un gráfico de\(f(x)=\frac{1}{\sqrt{x}}\) en Ejemplo\(\PageIndex{3}\)

2. La función\(f(x) = 1/x^2\) tiene una asíntota vertical en\(x=0\), como se muestra en la Figura\(\PageIndex{8}\), por lo que esta integral es una integral inadecuada. Dejemos de usar límites por un momento y procedamos sin reconocer la naturaleza impropia de la integral. Esto lleva a:\[\begin{align}\int_{-1}^1\frac1{x^2}\ dx &= -\frac1x\Big|_{-1}^1\\ &= -1 - (1)\\ &=-2 ! \end{align}\] Claramente el área en cuestión está por encima del\(x\) -eje, ¡sin embargo, el área supuestamente es negativa! ¿Por qué nuestra respuesta no coincide con nuestra intuición? Para responder a esto, evalúe la integral usando Definición\(\PageIndex{2}\). \[\begin{align} \int_{-1}^1\frac1{x^2}\ dx &= \lim_{t\to0^-}\int_{-1}^t \frac1{x^2}\ dx + \lim_{t\to0^+}\int_t^1\frac1{x^2}\ dx \\ &= \lim_{t\to0^-}-\frac1x\Big|_{-1}^t + \lim_{t\to0^+}-\frac1x\Big|_t^1\\ &= \lim_{t\to0^-}-\frac1t-1 + \lim_{t\to0^+} -1+\frac1t\\ &\Rightarrow \Big(\infty-1\Big)\ + \ \Big(- 1+\infty\Big).\end{align}\]Ninguno de los límites converge de ahí que la integral impropia original diverja. La respuesta sin sentido que obtuvimos al ignorar la naturaleza impropia de la integral es precisamente eso: sin sentido.

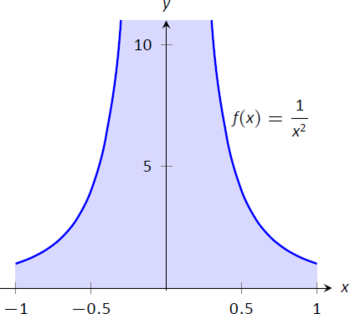
Figura\(\PageIndex{8}\): Un gráfico de\(f(x)=\frac{1}{x^2}\) en Ejemplo\(\PageIndex{3}\)

Comprender la convergencia y la divergencia

A menudo nos interesa saber simplemente si una integral inadecuada converge o no, y no necesariamente el valor de una integral convergente. Proporcionamos aquí varias herramientas que ayudan a determinar la convergencia o divergencia de integrales inadecuadas sin integrarse.

Nuestra primera herramienta es entender el comportamiento de las funciones de la forma\( \frac1{x\hskip1pt ^p}\).

Ejemplo\(\PageIndex{4}\): Improper integration of \(1/x^p\)

Determinar los valores de\(p\) para los cuales\(\int_1^\infty \frac1{x\hskip1pt ^p}\ dx\) converge.

Solución

Comenzamos integrando y luego evaluando el límite.

\[\begin{align} \int_1^\infty \frac1{x\hskip1pt ^p}\ dx &= \lim_{b\to\infty}\int_1^b\frac1{x\hskip1pt ^p}\ dx\\ &= \lim_{b\to\infty}\int_1^b x^{-p}\ dx \qquad \text{(assume $p\neq 1$)}\\&= \lim_{b\to\infty} \frac{1}{-p+1}x^{-p+1}\Big|_1^b\\ &= \lim_{b\to\infty} \frac{1}{1-p}\big(b\hskip1pt^{1-p}-1^{1-p}\big).\\\end{align}\]

¿Cuándo converge este límite, es decir, cuándo no es este límite\(\infty\)? Este límite converge precisamente cuando la potencia de\(b\) es menor que 0: cuando\(1-p<0 \Rightarrow 1<p\).

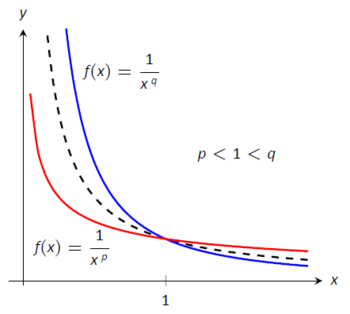
Figura\(\PageIndex{9}\): Trazando funciones de la forma\(1/x\,^p\) en Ejemplo\(\PageIndex{4}\)

Nuestro análisis muestra que si\(p>1\), entonces\(\int_1^\infty \frac1{x\hskip1pt ^p}\ dx \) converge. Cuando\(p<1\) la integral impropia diverge; mostramos en Ejemplo\(\PageIndex{1}\) que cuando\(p=1\) la integral también diverge.

\(\PageIndex{9}\)Gráficas de figuras\(y=1/x\) con una línea discontinua, junto con gráficas de\(y=1/x^p\)\(p<1\), y\(y=1/x^q\),\(q>1\). De alguna manera la línea discontinua forma una línea divisoria entre convergencia y divergencia.

El resultado de Example\(\PageIndex{4}\) proporciona una herramienta importante para determinar la convergencia de otras integrales. Un resultado similar se demuestra en los ejercicios sobre integrales inadecuadas de la forma\(\int_0^1\frac1{x\hskip1pt ^p}\ dx\). Estos resultados se resumen en la siguiente Idea Clave.

Idea Clave 21: Convergencia de Integrales Inadecuadas\(\int_1^\infty\frac1{x\hskip1pt ^p}\ dx\) and \(\int_0^1\frac1{x\hskip1pt ^p}\ dx\).

1. La integral inadecuada\(\int_1^\infty\frac1{x\hskip1pt ^p}\ dx\) converge cuando\(p>1\) y diverge cuando\(p\leq 1.\)
2. La integral inadecuada\(\int_0^1\frac1{x\hskip1pt ^p}\ dx\) converge cuando\(p<1\) y diverge cuando\(p\geq 1.\)

Una técnica básica para determinar la convergencia de integrales inadecuadas es comparar un integrando cuya convergencia es desconocida con un integrando cuya convergencia es conocida. A menudo utilizamos integrands de la forma\(1/x\hskip1pt ^p\) para compararlos a medida que se conoce su convergencia en ciertos intervalos. Esto se describe en el siguiente teorema.

Teorema\(\PageIndex{1}\): Direct Comparison Test for Improper Integrals

Dejar\(f\) y\(g\) ser continuo sobre\([a,\infty)\) dónde\(0\leq f(x)\leq g(x)\) para todos\(x\) adentro\([a,\infty)\).

1. Si\( \int_a^\infty g(x)\ dx\) converge, entonces\(\int_a^\infty f(x)\ dx\) converge.
2. Si\( \int_a^\infty f(x)\ dx\) diverge, entonces\( \int_a^\infty g(x)\ dx\) diverge.

Nota: Utilizamos el límite superior e inferior de “1" en Key Idea 21 para mayor comodidad. Se puede sustituir por cualquier\(a\) lugar\(a>0\).

Ejemplo\(\PageIndex{5}\): Determining convergence of improper integrals

Determinar la convergencia de las siguientes integrales inadecuadas.

1. \( \int_1^\infty e^{-x^2}\ dx\)
2. \( \int_3^\infty \frac{1}{\sqrt{x^2-x}}\ dx\)

Solución

1. La función\(f(x) = e^{-x^2}\) no tiene un antiderivado expresable en términos de funciones elementales, por lo que no podemos integrar directamente. Es comparable a\(g(x)=1/x^2\), y como se demuestra en la Figura\(\PageIndex{10}\),\(e^{-x^2} < 1/x^2\) on\([1,\infty)\). Sabemos por Key Idea 21 que\(\int_1^\infty \frac{1}{x^2}\ dx\) converge, de ahí que\(\int_1^\infty e^{-x^2}\ dx\) también converja.

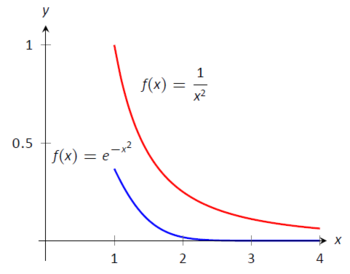
Figura\(\PageIndex{10}\): Gráficas de\(f(x) = e^{-x^2}\) y\(f(x)= 1/x^2\) en Ejemplo\(\PageIndex{6}\)

2. Tenga en cuenta que para grandes valores de\(x\),\( \frac{1}{\sqrt{x^2-x}} \approx \frac{1}{\sqrt{x^2}} =\frac{1}{x}\). Sabemos por Key Idea 21 y la nota posterior que\(\int_3^\infty \frac1x\ dx\) diverge, por lo que buscamos comparar el integrando original con\(1/x\).
   Es fácil ver que cuando\(x>0\), tenemos\(x = \sqrt{x^2} > \sqrt{x^2-x}\). Tomar recíprocas revierte la desigualdad, dando $$\ frac1x <\ frac1 {\ sqrt {x^2-x}}. $$
   Usando el teorema\(\PageIndex{1}\), concluimos que ya que\(\int_3^\infty\frac1x\ dx\) diverge,\(\int_3^\infty\frac1{\sqrt{x^2-x}}\ dx\) diverge también. La figura\(\PageIndex{11}\) ilustra esto.

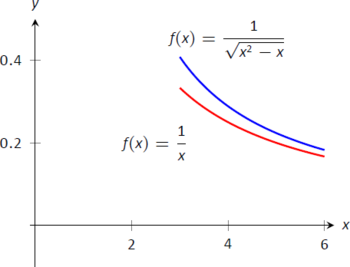
Figura\(\PageIndex{11}\): Gráficas de\(f(x) = 1/\sqrt{x^2-x}\) y\(f(x)= 1/x\) en Ejemplo\(\PageIndex{5}\)

Poder comparar integrales “desconocidas” con integrales “conocidas” es muy útil para determinar la convergencia. Sin embargo, algunos de nuestros ejemplos fueron un poco “demasiado agradables”. Por ejemplo, era conveniente que\(\frac{1}x < \frac{1}{\sqrt{x^2-x}}\), pero ¿y si los ""\(-x\) "fueran reemplazados por un"\(+2x+5\) “? Es decir, ¿qué podemos decir de la convergencia de\(\int_3^\infty\frac{1}{\sqrt{x^2+2x+5}}\ dx\)? Tenemos\(\frac{1}{x} > \frac1{\sqrt{x^2+2x+5}}\), entonces no podemos usar Teorema\(\PageIndex{1}\).

En casos como este (y muchos más) es útil emplear el siguiente teorema.

Teorema: Prueba de comparación de límites para integrales inadecuadas

Dejar\(f\) y\(g\) ser funciones continuas sobre\([a,\infty)\) dónde\(f(x)>0\) y\(g(x)>0\) para todos\(x\). Si

\[\lim_{x\to\infty} \frac{f(x)}{g(x)} = L,\qquad 0<L<\infty,\]

entonces

\[\int_a^\infty f(x)\ dx \quad \text{and} \quad \int_a^\infty g(x)\ dx\]

ambos convergen o ambos divergen.

Ejemplo\(\PageIndex{6}\): Determining convergence of improper integrals

Determinar la convergencia de\(\int_3^{\infty} \frac{1}{\sqrt{x^2+2x+5}}\ dx\).

Solución

A medida que\(x\) se hace grande, la función cuadrática dentro de la raíz cuadrada comenzará a comportarse de manera muy parecida\(y=x\). Así que comparamos\(\frac{1}{\sqrt{x^2+2x+5}}\)\ to\(\frac1x\) con la Prueba de Comparación de Límite:

$$\ lim_ {x\ a\ infty}\ frac {1/\ sqrt {x^2+2x+5}} {1/x} =\ lim_ {x\ a\ infty}\ frac {x} {\ sqrt {x^2+2x+5}}.\]

La evaluación inmediata de este límite retorna\(\infty/\infty\), una forma indeterminada. El uso de la Regla de L'Hôpital parece apropiado, pero en esta situación, no conduce a resultados útiles. (Alentamos al lector a emplear la Regla de L'Hôpital al menos una vez para verificar esto).

El problema es la función de raíz cuadrada. Para deshacernos de él, empleamos el siguiente hecho: Si\(\lim_{x\to c} f(x) = L\), entonces\(\lim_{x\to c} f(x)^2 = L^2\). (Esto es cierto cuando cualquiera\(c\) o\(L\) es\(\infty\).) Entonces consideramos ahora el límite\)

$$\ lim_ {x\ a\ infty}\ frac {x^2} {x^2+2x+5}.\]

Esto converge a 1, es decir, el límite original también convergió a 1. Como\(x\) se pone muy grande, la función\(\frac{1}{\sqrt{x^2+2x+5}}\) se parece mucho\(\frac1x.\) Ya que sabemos que\(\int_3^{\infty} \frac1x\ dx\) diverge, por la Prueba de Comparación de Límites sabemos que\(\int_3^\infty\frac{1}{\sqrt{x^2+2x+5}}\ dx\) también diverge. \(\PageIndex{12}\)Gráficas de figuras\(f(x)=1/\sqrt{x^2+2x+5}\) y\(f(x)=1/x\), ilustrando que a medida que\(x\) se agranda, las funciones se vuelven indistinguibles.

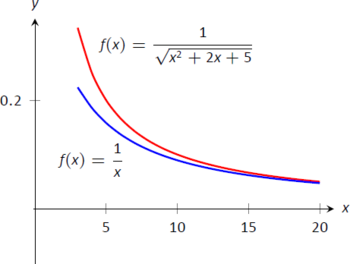
Figura\(\PageIndex{12}\): Gráfica\(f(x)=\frac{1}{\sqrt{x^2+2x+5}}\) y\(f(x)=\frac1x\) en Ejemplo\(\PageIndex{6}\).

Tanto las Pruebas de Comparación Directa como de Límites se dieron en términos de integrales a lo largo de un intervalo infinito. Hay versiones que se aplican a integrales inadecuadas con un rango infinito, pero como son un poco prolijas y un poco más difíciles de emplear, se omiten de este texto.

Este capítulo ha explorado muchas técnicas de integración. Aprendimos la Sustitución, que “deshace” la Regla de la Cadena de Diferenciación, así como la Integración por Partes, que “deshace” la Regla del Producto. Aprendimos técnicas especializadas para el manejo de funciones trigonométricas e introducimos las funciones hiperbólicas, las cuales están estrechamente relacionadas con las funciones trigonométricas. Todas las técnicas efectivamente tienen este objetivo en común: reescribir el integrando de una manera nueva para que el paso de integración sea más fácil de ver e implementar.

Como se dijo antes, la integración es, en general, difícil. Es fácil escribir una función cuya antiderivada es imposible de escribir en términos de funciones elementales, e incluso cuando una función sí tiene una antiderivada expresable por funciones elementales, puede ser realmente difícil descubrir qué es. El potente sistema de álgebra computacional Mathematica tiene aproximadamente 1,000 páginas de código dedicadas a la integración.

No dejes que esta dificultad te desanime. Hay un gran valor en el aprendizaje de las técnicas de integración, ya que permiten manipular una integral de manera que pueda iluminar un concepto para una mayor comprensión. También hay un gran valor en entender la necesidad de buenas técnicas numéricas: las Reglas Trapezoidales y Simpson son solo el comienzo de técnicas poderosas para aproximar el valor de la integración.

El siguiente capítulo destaca los usos de la integración. Generalmente no encontramos antiderivados por el bien de los antiderivados, sino porque proporcionan la solución a algún tipo de problema. El siguiente capítulo nos introduce a una serie de problemas diferentes cuya solución es proporcionada por la integración.

Colaboradores y Atribuciones

• Template:ContribApexCalc
• Template:ContribMarshall