6.6: Funciones hiperbólicas

Las funciones hiperbólicas son un conjunto de funciones que tienen muchas aplicaciones a las matemáticas, la física y la ingeniería. Entre muchas otras aplicaciones, se utilizan para describir la formación de anillos satélites alrededor de los planetas, para describir la forma de una cuerda que cuelga de dos puntos, y tienen aplicación a la teoría de la relatividad especial. Esta sección define las funciones hiperbólicas y describe muchas de sus propiedades, especialmente su utilidad para el cálculo.

Estas funciones son algunas veces referidas como las “funciones trigonométricas hiperbólicas” ya que hay muchas, muchas conexiones entre ellas y las funciones trigonométricas estándar. La figura\(\PageIndex{1}\) demuestra una de esas conexiones. Así como el coseno y el seno se utilizan para definir puntos en el círculo definido por\(x^2+y^2=1\), las funciones coseno hiperbólico y seno hiperbólico se utilizan para definir puntos en la hipérbola\(x^2-y^2=1\).

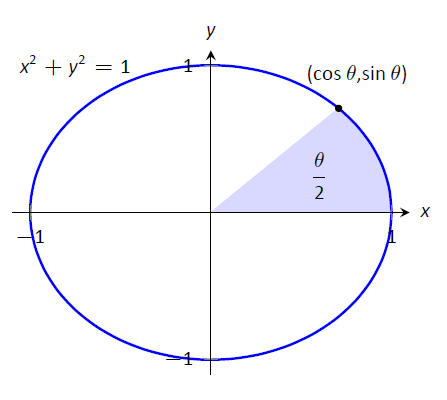
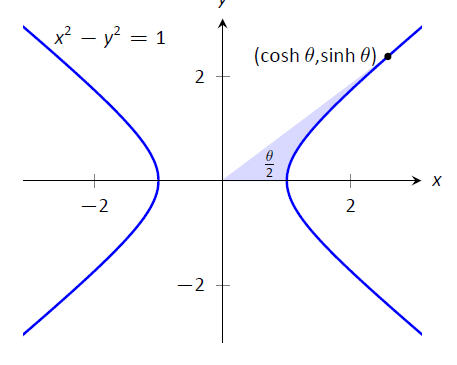
Figura\(\PageIndex{1}\): Uso de funciones trigonométricas para definir puntos en un círculo y funciones hiperbólicas para definir puntos en una hipérbola. En ellas se incluye el área de las regiones sombreadas.

Comenzamos con su definición.

Definición\(\PageIndex{1}\): Hyperbolic Functions

1. \( \cosh x = \frac{e^x+e^{-x}}2\)
2. \( \sinh x = \frac{e^x-e^{-x}}2\)
3. \(\tanh x = \frac{\sinh x}{\cosh x}\)
4. \( \text{sech} x = \frac{1}{\cosh x}\)
5. \( \text{csch} x = \frac{1}{\sinh x}\)
6. \( \coth x = \frac{\cosh x}{\sinh x}\)

Estas funciones hiperbólicas están graficadas en la Figura\(\PageIndex{2}\). En las gráficas de\(\cosh x\) y\(\sinh x\), gráficas de\(e^x/2\) y\(e^{-x}/2\) se incluyen con líneas discontinuas. Como\(x\) se pone “grande”,\(\cosh x\) y\(\sinh x\) cada acto como\(e^x/2\); cuando\(x\) es un gran número negativo,\(\cosh x\) actúa como\(e^{-x}/2\) mientras que $\ sinh x$ actúa como\(-e^{-x}/2\).

Observe los dominios de\(\tanh x\) y\(\text{sech} x\) son\((-\infty,\infty)\), mientras que ambos\(\coth x\) y\(\text{csch} x\) tienen asíntotas verticales en\(x=0\). También anotar los rangos de estas funciones, especialmente\(\tanh x\): as\(x\to\infty\), ambos\(\sinh x\) y\(\cosh x\) enfoque\(e^{-x}/2\), de ahí\(\tanh x\) se acerca\(1\).

El siguiente ejemplo explora algunas de las propiedades de estas funciones que tienen un notable parecido con las propiedades de sus contrapartes trigonométricas.

Nota de pronunciación: “cosh” rima con “dios”, “sinh” rima con “pellizco” y “tanh” rima con “rancho”.

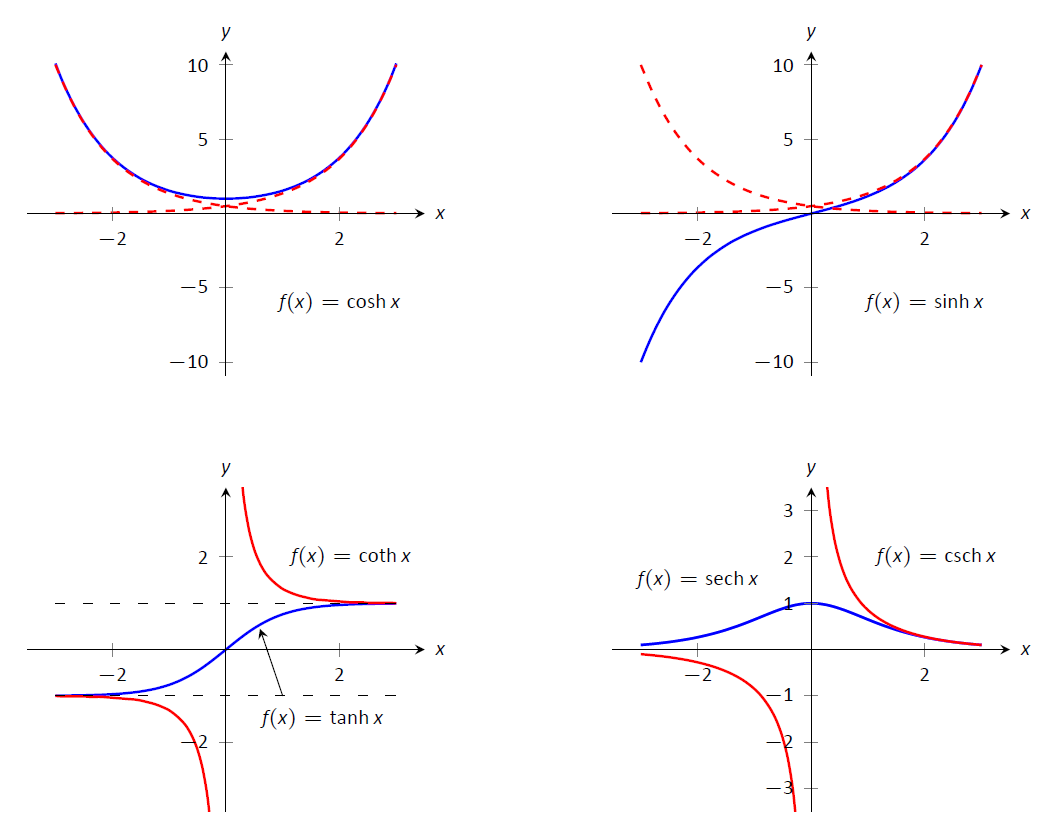
Figura\(\PageIndex{2}\): Gráficas de las funciones hiperbólicas.

Ejemplo\(\PageIndex{1}\): Exploring properties of hyperbolic functions

Utilice Definición\(\PageIndex{1}\) para reescribir las siguientes expresiones.

1. \(\cosh^2 x-\sinh^2x\)
2. \(\tanh^2 x+\text{sech}^2 x\)
3. \(2\cosh x\sinh x\)
4. \(\frac{d}{dx}\big(\cosh x\big)\)
5. \(\frac{d}{dx}\big(\sinh x\big)\)
6. \(\frac{d}{dx}\big(\tanh x\big)\)

Solución

1. \[\begin{align} \cosh^2x-\sinh^2x &= \left(\frac{e^x+e^{-x}}2\right)^2 -\left(\frac{e^x-e^{-x}}2\right)^2\\ &= \frac{e^{2x}+2e^xe^{-x} + e^{-2x}}4 - \frac{e^{2x}-2e^xe^{-x} + e^{-2x}}4\\ &= \frac44=1.\end{align}\]Entonces\(\cosh^2 x-\sinh^2x=1\).
2. \[\begin{align} \tanh^2 x+\text{sech}^2 x &=\frac{\sinh^2x}{\cosh^2 x} + \frac{1}{\cosh^2 x} \\ &= \frac{\sinh^2x+1}{\cosh^2 x}\qquad \text{Now use identity from #1.}\\ &= \frac{\cosh^2 x}{\cosh^2 x} = 1. \end{align}\]Entonces\(\tanh^2 x+\text{sech}^2 x=1\).
3. \[\begin{align} 2\cosh x\sinh x &= 2\left(\frac{e^x+e^{-x}}2\right)\left(\frac{e^x-e^{-x}}2\right) \\ &= 2 \cdot\frac{e^{2x} - e^{-2x}}4\\ &= \frac{e^{2x} - e^{-2x}}2 = \sinh (2x).\\ \end{align}\]Así\(2\cosh x\sinh x = \sinh (2x)\).
4. \[\begin{align} \frac{d}{dx}\big(\cosh x\big) &= \frac{d}{dx}\left(\frac{e^x+e^{-x}}2\right) \\ &= \frac{e^x-e^{-x}}2\\ &= \sinh x. \end{align}\]Entonces\(\frac{d}{dx}\big(\cosh x\big) = \sinh x.\)
5. \[\begin{align} \frac{d}{dx}\big(\sinh x\big) &= \frac{d}{dx}\left(\frac{e^x-e^{-x}}2\right) \\ &= \frac{e^x+e^{-x}}2\\ &= \cosh x. \end{align}\]Entonces\(\frac{d}{dx}\big(\sinh x\big) = \cosh x.\)
6. \[\begin{align} \frac{d}{dx}\big(\tanh x\big) &= \frac{d}{dx}\left(\frac{\sinh x}{\cosh x}\right) \\ &= \frac{\cosh x \cosh x - \sinh x \sinh x}{\cosh^2 x}\\ &= \frac{1}{\cosh^2 x}\\ &=\text{sech}^2 x. \end{align}\]Entonces\(\frac{d}{dx}\big(\tanh x\big) = \text{sech}^2 x.\)

La siguiente Idea Clave resume muchas de las identidades importantes relacionadas con las funciones hiperbólicas. Cada uno puede ser verificado refiriéndose de nuevo a Definición\(\PageIndex{1}\).

Idea clave 16: Propiedades útiles de la función hiperbólica

Identidades Básicas

1. \(\cosh^2x-\sinh^2x=1\)
2. \(\tanh^2x+\text{sech}^2x=1\)
3. \(\coth^2x-\text{csch}^2x = 1\)
4. \(\cosh 2x=\cosh^2x+\sinh^2x\)
5. \(\sinh 2x = 2\sinh x\cosh x\)
6. \(\cosh^2x = \frac{\cosh 2x+1}{2}\)
7. \(\sinh^2x=\frac{\cosh 2x-1}{2}\)

Derivados

1. \(\frac{d}{dx}\big(\cosh x\big) = \sinh x\)
2. \(\frac{d}{dx}\big(\sinh x\big) = \cosh x\)
3. \(\frac{d}{dx}\big(\tanh x\big) = \text{sech}^2 x\)
4. \(\frac{d}{dx}\big(\text{sech} x\big) = -\text{sech} x\tanh x\)
5. \(\frac{d}{dx}\big(\text{csch} x\big) = -\text{csch} x\coth x\)
6. \(\frac{d}{dx}\big(\coth x\big) = -\text{csch}^2x\)

Integrales

1. \(\int \cosh x\ dx = \sinh x+C\)
2. \(\int \sinh x\ dx = \cosh x+C\)
3. \(\int \tanh x\ dx = \ln(\cosh x) +C\)
4. \(\int \coth x\ dx = \ln|\sinh x\,|+C\)

Practicamos usando Key Idea 16

Ejemplo\(\PageIndex{2}\): Derivatives and integrals of hyperbolic functions

Evaluar las siguientes derivadas e integrales.

1. \(\frac{d}{dx}\big(\cosh 2x\big)\)
2. \(\int \text{sech}^2(7t-3)\ dt\)
3. \( \int_0^{\ln 2} \cosh x\ dx\)

Solución

1. Usando la Regla de Cadena directamente, tenemos\(\frac{d}{dx} \big(\cosh 2x\big) = 2\sinh 2x\).
   Solo para demostrar que funciona, usemos también la Identidad Básica que se encuentra en la Idea Clave 16:\(\cosh 2x = \cosh^2x+\sinh^2x\).
   \[\begin{align}\frac{d}{dx}\big(\cosh 2x\big) = \frac{d}{dx}\big(\cosh^2x+\sinh^2x\big) &= 2\cosh x\sinh x+ 2\sinh x\cosh x\\ &= 4\cosh x\sinh x.\end{align}\]Usando otra Identidad Básica, podemos ver eso\(4\cosh x\sinh x = 2\sinh 2x\). Obtenemos la misma respuesta de cualquier manera.
2. Empleamos sustitución, con\(u = 7t-3\) y\(du = 7dt\). Aplicando Ideas Clave 10 y 16 tenemos:
   $$\ int\ text {sech} ^2 (7t-3)\ dt =\ frac17\ tanh (7t-3) + C.$$
3. $$\ int_0^ {\ ln 2}\ cosh x\ dx =\ sinh x\ Big|_0^ {\ ln 2} =\ sinh (\ ln 2) -\ sinh 0 =\ sinh (\ ln 2). $$
   Podemos simplificar esta última expresión ya que\(\sinh x\) se basa en exponenciales:
   $$\ sinh (\ ln 2) =\ frac {e^ {\ ln 2} -e^ {-\ ln 2}} 2 =\ frac {2-1/2} {2} =\ frac34. $$

Funciones hiperbólicas inversas

Así como las funciones trigonométricas inversas son útiles en ciertas integraciones, las funciones hiperbólicas inversas son útiles con otras. La Figura 16 muestra las restricciones sobre los dominios para hacer cada función uno a uno y los dominios resultantes y rangos de sus funciones inversas. Sus gráficas se muestran en la Figura\(\PageIndex{3}\)

Debido a que las funciones hiperbólicas se definen en términos de funciones exponenciales, sus inversos pueden expresarse en términos de logaritmos como se muestra en la Idea Clave 17. A menudo es más conveniente referirse\(\sinh^{-1}x\) que a\(\ln\big(x+\sqrt{x^2+1}\big)\), especialmente cuando uno está trabajando en teoría y no necesita calcular valores reales. Por otro lado, cuando se necesitan cálculos, la tecnología suele ser útil pero muchas calculadoras manuales carecen de un\(\sinh^{-1}x\) botón\ textit {convenient}. (A menudo se puede acceder a él bajo un sistema de menús, pero no convenientemente.) En tal situación, la representación logarítmica es útil. No se anima al lector a memorizarlos, sino que sabe que existen y sabe utilizarlos cuando sea necesario.

Tabla\(\PageIndex{1}\): Gráficas de\(\cosh x\),\(\sinh x\) y sus inversos.

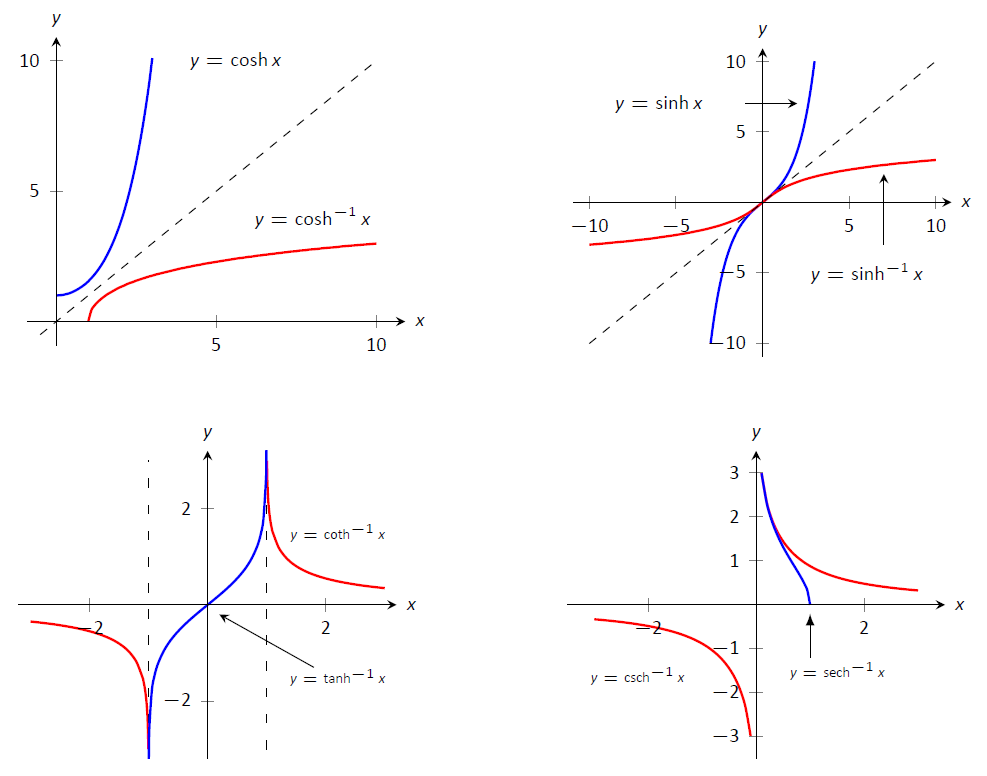
Figura\(\PageIndex{3}\): Gráficas de las funciones hiperbólicas y sus inversas.

Las siguientes Ideas Clave dan las derivadas e integrales relacionadas con las funciones hiperbólicas inversas. En la Idea Clave 19, se dan las representaciones de función tanto hiperbólica inversa como logarítmica de la antiderivada, con base en la Idea Clave 17. Nuevamente, estas últimas funciones suelen ser más útiles que las primeras. Observe cómo las funciones hiperbólicas inversas se pueden usar para resolver integrales que usamos Sustitución trigonométrica para resolver en la Sección 6.4.

Clave IDa 17: Definiciones logarítmicas de las funciones hiperbólicas inversas.

1. \(\cosh^{-1}x=\ln\big(x+\sqrt{x^2-1}\big);\ x\geq1\)
2. \(\tanh^{-1}x = \frac12\ln\left(\frac{1+x}{1-x}\right);\ |x|<1\)
3. \(\text{sech}^{-1}x = \ln\left(\frac{1+\sqrt{1-x^2}}x\right);\ 0<x\leq1\)
4. \(\sinh^{-1}x = \ln\big(x+\sqrt{x^2+1}\big)\)
5. \(\coth^{-1}x = \frac12\ln\left(\frac{x+1}{x-1}\right);\ |x|>1\)
6. \(\text{csch}^{-1}x = \ln\left(\frac1x+\frac{\sqrt{1+x^2}}{|x|}\right);\ x\neq0\)

Idea clave 18: Derivadas que involucran funciones hiperbólicas inversas

1. \(\frac{d}{dx}\big(\cosh^{-1} x\big) = \frac{1}{\sqrt{x^2-1}};\ x>1\)
2. \(\frac{d}{dx}\big(\sinh^{-1} x\big) = \frac{1}{\sqrt{x^2+1}}\)
3. \(\frac{d}{dx}\big(\tanh^{-1} x\big) = \frac{1}{1-x^2};\ |x|<1\)
4. \(\frac{d}{dx}\big(\text{sech}^{-1} x\big) = \frac{-1}{x\sqrt{1-x^2}}; 0<x<1\)
5. \(\frac{d}{dx}\big(\text{csch}^{-1} x\big) = \frac{-1}{|x|\sqrt{1+x^2}};\ x\neq0\)
6. \(\frac{d}{dx}\big(\coth^{-1} x\big) = \frac{1}{1-x^2};\ |x|>1\)

Idea Clave 19: Integrales que involucran funciones hiperbólicas inversas

1. \(\int \frac{1}{\sqrt{x^2-a^2}}\ dx\)\(=\qquad \cosh^{-1}\left(\frac xa\right)+C;\ 0<a<x\)\(\quad=\ln\Big|x+\sqrt{x^2-a^2}\Big|+C\)
2. \(\int \frac{1}{\sqrt{x^2+a^2}}\ dx\)\(=\qquad \sinh^{-1}\left(\frac xa\right)+C;\ a>0\)\(\qquad=\ln\Big|x+\sqrt{x^2+a^2}\Big|+C\)
3. \(\int \frac{1}{a^2-x^2}\ dx\)\(=\qquad \left\{\begin{array}{ccc} \frac1a\tanh^{-1}\left(\frac xa\right)+C & & x^2<a^2 \\ \\\frac1a\coth^{-1}\left(\frac xa\right)+C & & a^2<x^2 \end{array}\right.\)\(\quad=\frac1{2a}\ln\left|\frac{a+x}{a-x}\right|+C\)
4. \(\int \frac{1}{x\sqrt{a^2-x^2}}\ dx \)\(=\qquad -\frac1a\text{sech}^{-1}\left(\frac xa\right)+C;\ 0<x<a\)\(\quad= \frac1a \ln\left(\frac{x}{a+\sqrt{a^2-x^2}}\right)+C \)
5. \(\int \frac{1}{x\sqrt{x^2+a^2}}\ dx\)\(=\qquad -\frac1a\text{csch}^{-1}\left|\frac xa\right| + C;\ x\neq 0,\ a>0\)\(\quad= \frac1a \ln\left|\frac{x}{a+\sqrt{a^2+x^2}}\right|+C\)

Practicamos usando las fórmulas derivadas e integrales en el siguiente ejemplo.

Ejemplo\(\PageIndex{3}\): Derivatives and integrals involving inverse hyperbolic functions

Evalúe lo siguiente.

1. \( \frac{d}{dx}\left[\cosh^{-1}\left(\frac{3x-2}{5}\right)\right]\)
2. \( \int\frac{1}{x^2-1}\ dx\)
3. \( \int \frac{1}{\sqrt{9x^2+10}}\ dx\)

Solución

1. Aplicando la Idea Clave 18 con la Regla de Cadena da:
   $$\ frac {d} {dx}\ left [\ cosh^ {-1}\ left (\ frac {3x-2} 5\ right)\ right] =\ frac {1} {\ sqrt {\ left (\ frac {3x-2} 5\ right) ^2-1}}\ cdot\ frac35. $$
2. Multiplicar el numerador y denominador por\((-1)\) da:\( \int \frac{1}{x^2-1}\ dx = \int \frac{-1}{1-x^2}\ dx\). La segunda integral se puede resolver con una aplicación directa del ítem #3 de Key Idea 19, con\(a=1\). Así\[ \begin{align} \int \frac{1}{x^2-1}\ dx &= -\int \frac{1}{1-x^2}\ dx \\ &= \left\{\begin{array}{ccc} -\tanh^{-1}\left(x\right)+C & & x^2<1 \\ \\-\coth^{-1}\left(x\right)+C & & 1<x^2 \end{array}\right. \\ &=-\frac12\ln\left|\frac{x+1}{x-1}\right|+C\\ &=\frac12\ln\left|\frac{x-1}{x+1}\right|+C. \end{align}\]

   Debemos señalar que este problema exacto se resolvió al inicio de la Sección 6.5. En ese ejemplo la respuesta se dio como\(\frac12\ln|x-1|-\frac12\ln|x+1|+C.\) Note que esto es equivalente a la respuesta dada en Ecuación\(\PageIndex{29}\), as\(\ln(a/b) = \ln a - \ln b\).

3. Esto requiere una sustitución, entonces se puede aplicar el ítem #2 de Key Idea 19.

   Vamos\(u = 3x\), de ahí\(du = 3dx\). Tenemos
   \[\int \frac{1}{\sqrt{9x^2+10}}\ dx = \frac13\int\frac{1}{\sqrt{u^2+10}}\ du. \]
   Nota\(a^2=10\), de ahí\(a = \sqrt{10}.\) Ahora aplicar la regla integral.
   \[\begin{align} &= \frac13 \sinh^{-1}\left(\frac{3x}{\sqrt{10}}\right) + C \\&= \frac13 \ln \Big|3x+\sqrt{9x^2+10}\Big|+C. \end{align}\]

Esta sección cubre mucho terreno. Se introdujeron nuevas funciones, junto con algunas de sus identidades fundamentales, sus derivados y antiderivados, sus inversos y los derivados y antiderivados de estos inversos. Se presentaron cuatro Ideas Clave, cada una con bastante información.

No vea esta sección como una fuente de información a memorizar, sino como una referencia para la futura resolución de problemas. Key Idea 19 contiene quizás la información más útil. Conocer las formas de integración ayuda a evaluar y entender cómo usar la respuesta hiperbólica inversa y la respuesta logarítmica.

La siguiente sección toma un breve descanso de demostrar nuevas técnicas de integración. En cambio, demuestra una técnica de evaluación de límites que devuelven formas indeterminadas. Esta técnica será útil en la Sección 6.8, donde surgirán límites en la evaluación de ciertas integrales definidas.

Colaboradores y Atribuciones

• Template:ContribApexCalc
• Template:ContribMarshall